


2022-2023学年江苏省张家港市梁丰初级中学七下数学期末经典试题含答案
展开2022-2023学年江苏省张家港市梁丰初级中学七下数学期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知反比例函数![]() ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当![]() 时,
时,![]() D.当
D.当![]() 时,y随着x的增大而增大
时,y随着x的增大而增大
2.若点A(3,2)与B(-3,m)关于原点对称,则m的值是( )
A.3 B.-3 C.2 D.-2
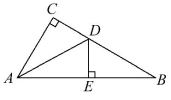
3.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC= ( )
A.![]() B.2 C.3 D.
B.2 C.3 D.![]() +2
+2
4.分式![]() 的值为0,则
的值为0,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列命题正确的个数是( )
(1)若x2+kx+25是一个完全平方式,则k的值等于10;(2)正六边形的每个内角都等于相邻外角的2倍;(3)一组对边平行,一组对角相等的四边形是平行四边形;(4)顺次连结四边形的四边中点所得的四边形是平行四边形
A.1 B.2 C.3 D.4
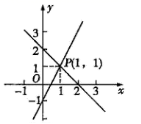
6.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.某班抽6名同学参加体能测试,成绩分别是1,90,75,75,1,1.则这组同学的测试成绩的中位数是( )
A.75 B.1 C.85 D.90
8.下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的四边形是矩形
C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形
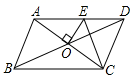
9.如图,▱ABCD 的周长为 16 cm,AC,BD 相交于点 O,OE⊥AC交 AD 于点 E,则△DCE 的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
10.下列数据中不能作为直角三角形的三边长的是( )
A.1、![]() B.
B.![]() C.5、12、13 D.1、2、3
C.5、12、13 D.1、2、3
11.如图,每个小正方形边长均为1,则下列图中的阴影三角形与左图中![]() 相似的是( )
相似的是( )
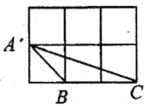
A.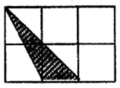 B.
B.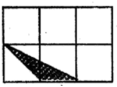
C.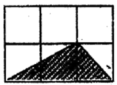 D.
D.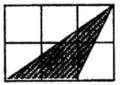
12.下列说法正确的是( )
A.某个对象出现的次数称为频率 B.要了解某品牌运动鞋使用寿命可用普查
C.没有水分种子发芽是随机事件 D.折线统计图用于表示数据变化的特征和趋势
二、填空题(每题4分,满分20分,将答案填在答题纸上)
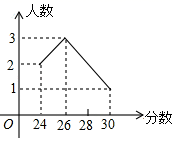
13.在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是___分.
14.若关于![]() 的分式方程
的分式方程![]() 有增根,则
有增根,则![]() 的值为__________.
的值为__________.
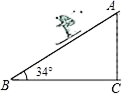
15.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了_____米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
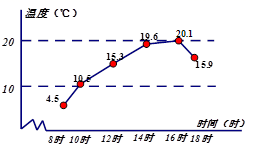
16.已知杭州市某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数是 .
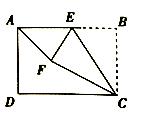
17.如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点,将
边上一点,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,当
处,当![]() 为直角三角形时,
为直角三角形时,![]() ________.
________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
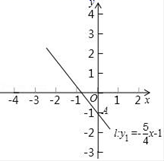
18.(5分)如图,直线l:y1=﹣![]() x﹣1与y轴交于点A,一次函数y2=
x﹣1与y轴交于点A,一次函数y2=![]() x+3图象与y轴交于点B,与直线l交于点C,
x+3图象与y轴交于点B,与直线l交于点C,
(1)画出一次函数y2=![]() x+3的图象;
x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
19.(5分)我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
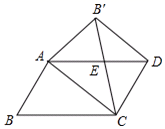
(发现与证明)▱ABCD中,AB≠BC,将△ABC沿AC翻折至△AB`C,连结B`D.
结论1:△AB`C与▱ABCD重叠部分的图形是等腰三角形;结论2:B`D∥AC;
(1)请证明结论1和结论2;
(应用与探究)
(2)在▱ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB`C,连接B`D![]() 若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
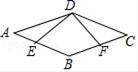
20.(8分)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
21.(10分)解不等式组: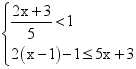 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
![]()
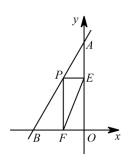
22.(10分)已知:如图,已知直线AB的函数解析式为 ![]() ,AB与y轴交于点 ,与x轴交于点 .
,AB与y轴交于点 ,与x轴交于点 .
(1)在答题卡上直接写出A,B两点的坐标;
(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点 F,连接EF.问:
①若![]() 的面积为 S,求S关于a的函数关系式;
的面积为 S,求S关于a的函数关系式;
② 是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
23.(12分)如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
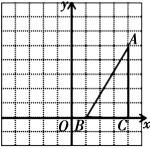
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求在平移过程中线段AB扫过的面积.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、D
3、C
4、A
5、C
6、D
7、B
8、C
9、C
10、D
11、B
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、![]()
15、1.
16、15.6
17、3或6
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)画图见解析;(1)点C坐标为(﹣1,![]() );(3)x<﹣1.
);(3)x<﹣1.
19、
20、(1)证明见解析;(2)证明见解析.
21、不等式组的解集是![]() ,数轴表示见解析.
,数轴表示见解析.
22、(1)![]() ;(2)①
;(2)①![]() (-5≤a≤0); ②存在,
(-5≤a≤0); ②存在,![]()
23、(1)图见解析,![]() ;(2)25
;(2)25
江苏省张家港市梁丰初级中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案: 这是一份江苏省张家港市梁丰初级中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列说法,如图,正六边形内接于,连接,如图所示的几何体的左视图是等内容,欢迎下载使用。
2023-2024学年江苏省苏州市张家港市梁丰初级中学九上数学期末联考试题含答案: 这是一份2023-2024学年江苏省苏州市张家港市梁丰初级中学九上数学期末联考试题含答案,共7页。试卷主要包含了抛物线与坐标轴的交点个数为,已知是方程的一个解,则的值是等内容,欢迎下载使用。
江苏省张家港市梁丰中学2023-2024学年数学九上期末调研模拟试题含答案: 这是一份江苏省张家港市梁丰中学2023-2024学年数学九上期末调研模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,以下事件为必然事件的是等内容,欢迎下载使用。












