


2022-2023学年江苏省扬州市江都区邵凡片七年级数学第二学期期末达标检测模拟试题含答案
展开2022-2023学年江苏省扬州市江都区邵凡片七年级数学第二学期期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 匀速运动,设点
匀速运动,设点![]() 走过的路程为
走过的路程为![]() ,
,![]() 的面积为
的面积为![]() ,能正确反映
,能正确反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
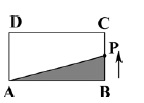
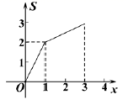
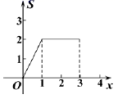
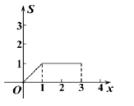
A. B. C. D.
2.设max{a,b}表示a,b两个数中的最大值,例如max{0,2}=2,max{12,8}=12,则关于x的函数y=max{2x,x+2}可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长为( )
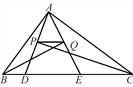
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
4.以下说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.有三个内角相等的四边形是矩形
D.对角线垂直且相等的四边形是正方形
5.使![]() 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A.x≤3 B.x<3 C.x≥3 D.x>3
6.欧几里得是古希腊数学家,所著的《几何原本》闻名于世.在《几何原本》中,形如x2+ax=b2的方程的图解法是:如图,以![]() 和b为直角边作Rt△ABC,再在斜边上截取BD=
和b为直角边作Rt△ABC,再在斜边上截取BD=![]() ,则图中哪条线段的长是方程x2+ax=b2的解?答:是( )
,则图中哪条线段的长是方程x2+ax=b2的解?答:是( )
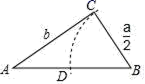
A.AC B.AD C.AB D.BC
7.在平面直角坐标系中,下列各点位于第四象限的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.点A(m+4,m)在平面直角坐标系的x轴上,则点A关于y轴对称点的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若化简![]() 的结果为
的结果为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.一切实数 B.![]() C.
C.![]() D.
D.![]()
10.在直角三角形中,两条直角边的长分别为12和5,则斜边上的中线长是( )
A.6.5 B.8.5 C.13 D.![]()
11.用配方法解一元二次方程x2-8x+3=0,此方程可化为( )
A.(x-4)2=13 B.(x+4)2=13 C.(x-4)2=19 D.(x+4)2=19
12.如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长为( )
的周长为( )
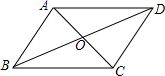
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.分解因式:x3-3x=______.
14.将一个有80个数据的一组数分成四组,绘出频数分布直方图,已知各小长方形的高的比为![]() ,则第二小组的频数为______.
,则第二小组的频数为______.
15.在△ABC ,∠BAC 90, AB AC 4, O 是 BC 的中点, D 是腰 AB 上一动点,把△DOB 沿 OD 折叠得到 △DOB' ,当 ∠ADB' 45 时, BD 的长度为_____.
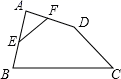
16.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为_____.
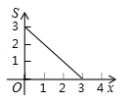
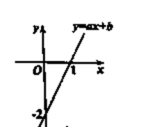
17.一次函数![]() 的图象如图所示,不等式
的图象如图所示,不等式![]() 的解集为__________.
的解集为__________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由![]() 两工程队先后接力完成.
两工程队先后接力完成.![]() 工作队每天整治12米,
工作队每天整治12米,![]() 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:![]() 乙:
乙: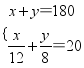
根据甲、乙两名同学所列的方程组,请你分别指出未知数![]() 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示________________,y表示_______________;
乙:x表示________________,y表示_______________.
(2)求![]() 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
19.(5分)(1)分解因式:①![]() ②
②![]()
(2)解不等式组,并把解集在数轴上表示出来. 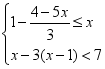
20.(8分)已知方程组![]() ,当m为何值时,x>y?
,当m为何值时,x>y?
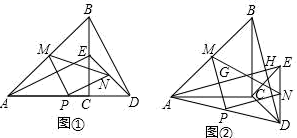
21.(10分)如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.
22.(10分)某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支.
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
23.(12分)如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
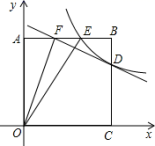
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
(4)若点P是x轴上的动点,点Q是(1)中的反比例函数在第一象限图象上的动点,且使得△PDQ为等腰直角三角形,请求出点P的坐标.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、A
3、C
4、B
5、C
6、B
7、D
8、A
9、B
10、A
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、2
15、![]() .
.
16、140°
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)甲:![]() 表示
表示![]() 工程队工作的天数,
工程队工作的天数,![]() 表示
表示![]() 工程队工作的天数;
工程队工作的天数;
乙:![]() 表示
表示![]() 工程队整治河道的米数,
工程队整治河道的米数,![]() 表示
表示![]() 工程队整治河道的米数.
工程队整治河道的米数.
(2)![]() 两工程队分别整治了60米和120米.
两工程队分别整治了60米和120米.
19、 (1)① ![]() ;②
;②![]() ;(2)
;(2)![]()
20、![]() .
.
21、 (1)证明见解析;(2)成立,理由见解析.
22、(1)15元;(2)1支.
23、(1)y=![]() ;(2)点F的坐标为(2,4);(3)∠AOF=
;(2)点F的坐标为(2,4);(3)∠AOF=![]() ∠EOC,理由见解析;(4)P的坐标是(
∠EOC,理由见解析;(4)P的坐标是(![]() ,0)或(-5,0)或(
,0)或(-5,0)或(![]() ,0)或(5,0)
,0)或(5,0)
江苏省扬州市江都区邵凡片2023-2024学年九上数学期末考试试题含答案: 这是一份江苏省扬州市江都区邵凡片2023-2024学年九上数学期末考试试题含答案,共8页。试卷主要包含了已知反比例函数y=等内容,欢迎下载使用。
江苏省扬州市江都区邵凡片2023-2024学年八上数学期末复习检测模拟试题含答案: 这是一份江苏省扬州市江都区邵凡片2023-2024学年八上数学期末复习检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,64的平方根是,下列命题是真命题的是,在式子,,,中,分式的个数是,解方程去分母得等内容,欢迎下载使用。
江苏省扬州市江都区邵樊片2023-2024学年八上数学期末质量检测试题含答案: 这是一份江苏省扬州市江都区邵樊片2023-2024学年八上数学期末质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列能用平方差公式计算的是,估算的值在,若函数是正比例函数,则的值为等内容,欢迎下载使用。












