


2022-2023学年江苏省张家港市梁丰初级中学数学七下期末达标检测模拟试题含答案
展开2022-2023学年江苏省张家港市梁丰初级中学数学七下期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.下列根式中是最简根式的是( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
2.下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.![]() ,
,![]() ,
,![]() C.3,4,6 D.4,5,6
C.3,4,6 D.4,5,6
3.下列多项式中能用完全平方公式分解的是( )
A.x2-x+1 B.a2+a+![]() C.1- 2x+x2 D.-a2+b2-2ab
C.1- 2x+x2 D.-a2+b2-2ab
4.一元二次方程![]() 的根为( )
的根为( )
A.0 B.3 C.0或﹣3 D.0或3
5.一种药品经过两次降价,药价从每盒60元下调至每盒48.6元,则平均每次降价的百分比是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
6.下列二次根式中是最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为()
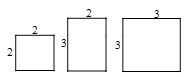
A.6 B.7 C.8 D.9
8.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在![]() 的( )
的( )
A.三边中垂线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
9.下列二次根式中,不是最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如果一组数据![]() ,
,![]() ,0,1,x,6,9,12的平均数为3,则x为
,0,1,x,6,9,12的平均数为3,则x为![]()
![]()
A.2 B.3 C.![]() D.1
D.1
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在一个不透明的盒子中装有n个球,它们除了颜色之外其它都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是_____.
12.小李掷一枚均匀的硬币![]() 次,出现的结果如下:正、反、正、反、反、反、正、正、反、反、反、正,则出现“反面朝上”的频率为______.
次,出现的结果如下:正、反、正、反、反、反、正、正、反、反、反、正,则出现“反面朝上”的频率为______.
13.把直线y=﹣x﹣3向上平移m个单位,与直线y=2x+4的交点在第二象限,则m的取值范围是_____.
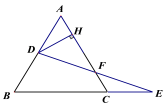
14.如图,已知等边三角形ABC的边长为7,点D为AB上一点,点E在BC的延长线上,且CE=AD,连接DE交AC于点F,作DH⊥AC于点H,则线段HF的长为 ____________.
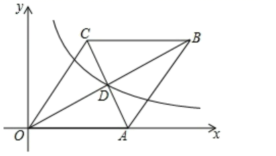
15.如图,在平面直角坐标系中,菱形![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() 与
与![]() 交于点
交于点![]() (4,2),反比例函数
(4,2),反比例函数![]() 的图象经过点
的图象经过点![]() .若将菱形
.若将菱形![]() 向左平移
向左平移![]() 个单位,使点
个单位,使点![]() 落在该反比例函数图象上,则
落在该反比例函数图象上,则![]() 的值为_____________.
的值为_____________.
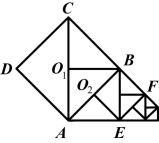
16.如图,正方形ABCD边长为1,若以正方形的边AB为对角线作第二个正方形AEBO1,再以边BE为对角线作第三个正方形EFBO2……如此作下去,则所作的第n个正方形面积Sn=________
三、解下列各题(本大题共8小题,共72分)
17.(8分)小明要把一篇社会调查报告录入电脑,当他以100字/分的速度录入文字时,经240分钟能完成录入,设他录入文字的速度为v字/分时,完成录入的时间为t分。
(1)求t与v之间的函数表达式;
(2)要在3h内完成录入任务,小明每分钟至少应录入多少个字?
18.(8分)如图,在平面直角坐标系中,![]() 各顶点的坐标分别为
各顶点的坐标分别为![]()
![]()
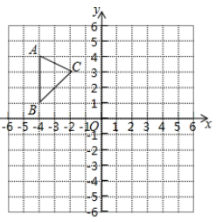
(1)作出![]() 关于原点
关于原点![]() 成中心对称的
成中心对称的![]() .
.
(2)作出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 若把点
若把点![]() 向右平移
向右平移![]() 个单位长度后,落在
个单位长度后,落在![]() 的内部(不包括顶点和边界),
的内部(不包括顶点和边界),![]() 的取值范围,
的取值范围,
19.(8分)如图,平行四边形![]() 中,
中,![]() 在
在![]() 边上,
边上,![]() ,
,![]() 为平行四边形
为平行四边形![]() 外一点,连接
外一点,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,且
,且![]() .
.
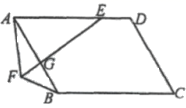
(1)若![]() ,
,![]() ,求平行四边形
,求平行四边形![]() 的面积;
的面积;
(2)求证:![]() .
.
20.(8分)甲、乙两名射击运动员进行射击比赛,两人在相同的条件下各射击10次,射击的成绩如图所示.根据图中信息,解答下列问题:
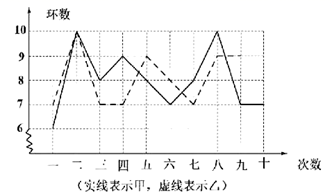
(1)算出乙射击成绩的平均数;
(2)经计算,甲射击成绩的平均数为8,乙射击成绩的方差为1.2,请你计算出甲射击成绩的方差,并判断谁的射击成绩更加稳定.
21.(8分)计算(![]() +
+![]() )﹣(
)﹣(![]() +6)
+6)
22.(10分)阅读下面的解题过程,解答后面的问题:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 点的坐标;
点的坐标;
解:分别过![]() ,
,![]() 做
做![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 做
做![]() 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图![]() 所示,设
所示,设![]() ,则
,则![]() ,
,![]() ,
,![]()
由图![]() 可知:
可知:
![]()
![]()
![]() 线段
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]()
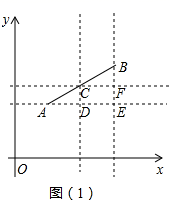
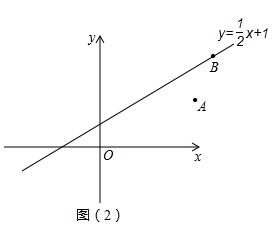
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为
(2)平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,利用中点坐标公式求点
,利用中点坐标公式求点![]() 的坐标。
的坐标。
(3)如图![]() ,点
,点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在函数
在函数![]() 的图象上 ,以
的图象上 ,以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点,且以
四个点为顶点,且以![]() 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的![]() 点坐标。
点坐标。
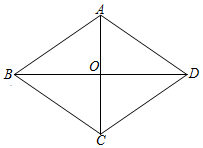
23.(10分)如图,菱形![]() 的对角线
的对角线![]() 和
和![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.
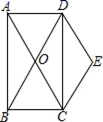
24.(12分)如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、C
4、C
5、B
6、A
7、C
8、A
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、![]()
13、1<m<1.
14、![]()
15、1
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ,(2)小明每分钟至少应录入134个字,才能在3h内完成录入任务.
,(2)小明每分钟至少应录入134个字,才能在3h内完成录入任务.
18、(1)见解析;(2)见解析,![]()
19、 (1)![]() ;(2)证明见解析.
;(2)证明见解析.
20、(1)8;(2)乙.
21、![]()
22、 (1)线段![]() 的中点坐标是
的中点坐标是![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)符合条件的
;(3)符合条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
23、![]()
24、(1)证明见解析;(1)![]() .
.
江苏省张家港市梁丰初级中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案: 这是一份江苏省张家港市梁丰初级中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列说法,如图,正六边形内接于,连接,如图所示的几何体的左视图是等内容,欢迎下载使用。
江苏省张家港市梁丰中学2023-2024学年数学九上期末调研模拟试题含答案: 这是一份江苏省张家港市梁丰中学2023-2024学年数学九上期末调研模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,以下事件为必然事件的是等内容,欢迎下载使用。
2023-2024学年江苏省苏州市张家港市梁丰高级中学数学八上期末检测试题含答案: 这是一份2023-2024学年江苏省苏州市张家港市梁丰高级中学数学八上期末检测试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,化简的结果是,分式的值为0,则的值是,如果,那么代数式的值是.,在,,,中分式的个数有等内容,欢迎下载使用。












