2022-2023学年山东省淄博沂源县联考七下数学期末学业水平测试试题含答案

2022-2023学年山东省淄博沂源县联考七下数学期末学业水平测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生须知：

1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)

1．如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为（　　）

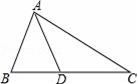
A．35° B．40° C．45° D．50°

2．在我县“我的中国梦”演讲比赛中，有7名同学参加了比赛，他们最终决赛的成绩各不相同．其中一名学生想要知道自己是否进入前3名，不仅要知道自己的分数，还得知道这7名学生成绩的（     ）

A．众数 B．方差 C．平均数 D．中位数

3．设直线y＝kx+6和直线y＝（k+1）x+6（k是正整数）及x轴围成的三角形面积为Sk（k＝1，2，3，…，8），则S1+S2+S3+…+S8的值是（　　）

A． B． C．16 D．14

4．对于函数y=﹣5x+1，下列结论：

①它的图象必经过点（﹣1，5）

②它的图象经过第一、二、三象限

③当x＞1时，y＜0

④y的值随x值的增大而增大，

其中正确的个数是（　　）

A．0 B．1 C．2 D．3

5．要从甲、乙、丙三名学生中选出一名学生参加数学竞赛，对这三名学生进行了10次数学测试，经过数据分析，3人的平均成绩均为92分，甲的方差为0.024、乙的方差为0.08、丙的方差为0.015，则这10次测试成绩比较稳定的是（　　）

A．甲 B．乙 C．丙 D．无法确定

6．在平面直角坐标系中，分别过点A（m，0），B（m＋2，0）作垂直于x轴的直线l1和l2，探究直线 l1、l2与函数y=的图像（双曲线）之间的关系，下列结论错误的是(   )

A．两条直线中总有一条与双曲线相交

B．当 m＝1 时，两条直线与双曲线的交点到原点的距离相等

C．当 m＜0 时，两条直线与双曲线的交点都在 y 轴左侧

D．当 m＞0 时，两条直线与双曲线的交点都在 y 轴右侧

7．以下列长度（单位：cm）为边长的三角形是直角三角形的是（   ）

A．3,4,5 B．1,2,3 C．5,7,9 D．6,10,12

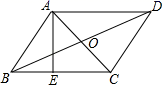
8．如图，平行四边形ABCD的对角线AC与BD相交于点O，AE⊥BC于E，AB＝，AC＝2，BD＝4，则AE的长为（　　）

A． B． C． D．

9．下列图形既是轴对称图形，又是中心对称图形的是（     ）

A．三角形 B．圆 C．角 D．平行四边形

10．若a＞b，则下列式子正确的是（　　）

A．a+2＜b+2 B．﹣2a＞﹣2b C．a﹣2＞b﹣2 D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．计算： =_______________．

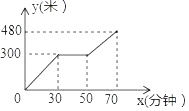
12． “五一”期间，小红到某景区登山游玩，小红上山时间x（分钟）与走过的路程y（米）之间的函数关系如图所示，在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山，若小红上山过程中与小卉恰好有两次相遇，则小卉上山平均速度v（米/分钟）的取值范围是_____．

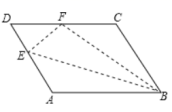
13．如图所示，平行四边形中，点在边上，以为折痕，将向上翻折，点正好落在上的处，若的周长为8，的周长为22，则的长为__________．

14．对于函数y＝（m﹣2）x+1，若y随x的增大而增大，则m的取值范围_____．

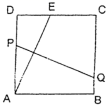
15．如图，将一块边长为 12 cm 正方形纸片 ABCD 的顶点 A 折叠至DC 边上的 E 点，使 DE＝5，折痕为 PQ，则 PQ 的长为_________cm．

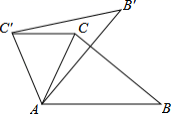
16．如图所示，在中，，在同一平面内，将绕点逆时针旋转到△的位置，使，则___．

三、解下列各题(本大题共8小题，共72分)

17．（8分）申思同学最近在网上看到如下信息：

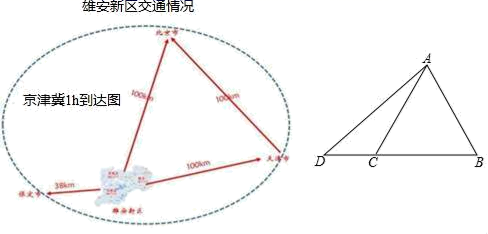
总书记明确指示，要重点打造北京非首都功能疏解集中承载地，在河北适合地段规划建设一座以新发展理念引领的现代新型城区．雄安新区不同于一般意义上的新区，其定位是重点承接北京疏解出的与去全国政治中心、文化中心、国际交往中心、科技创新中心无关的城市功能，包括行政事业单位、总部企业、金融机构、高等院校、科研院所等．右图是北京、天津、保定和雄安新区的大致交通图，其中保定、天津和雄安新区可近似看作在一条直线上．申思同学想根据图中信息求出北京和保定之间的大致距离．

他先画出如图示意图，其中AC＝AB＝BC＝100，点C在线段BD上，他把CD近似当作40，来求AD的长．

请帮申思同学解决这个问题．

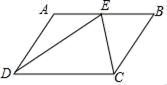
18．（8分）如图，已知点E在平行四边形ABCD的边AB上，设＝，再用图中的线段作向量．

(1)写出平行的向量　   　；

(2)试用向量表示向量；

(3)求作：.

19．（8分）已知平面直角坐标系中有一点（，）．

（1）若点在第四象限，求的取值范围；

（2）若点到轴的距离为3，求点的坐标．

20．（8分）潮州市某学校为了改善办学条件，购置一批电子白板和台式电脑合共24台.经招投标，一台电子白板每台9000元，一台台式电脑每台3000元，设学校购买电子白板和台式电脑总费用为元，购买了台电子白板，并且台式电脑的台数不超过电子白板台数的3倍.

(1)请求出与的函数解析式，并直接写出的取值范围

(2)请问当购买多少台电子白板时，学校购置电子白板和台式电脑的总费用最少，最少多少钱？

21．（8分）计算下列各题：

（1）                 

（2）

22．（10分）甲、乙两班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如表，请根据表中数据解答下列问题

（1）分别写出甲、乙两班选手进球数的平均数、中位数与众数；

（2）如果要从这两个班中选出一个班级参加学校的投篮比赛，争取夺得总进球团体的第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？

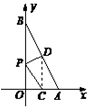
23．（10分）一次函数y=kx＋b的图象与x、y轴分别交于点A(2，0)，B(0，4)．

(1)求该函数的解析式；

(2)O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点的坐标．

24．（12分）解方程：（1）x（2x+3）＝4x+6

计算：（2）

（3）

参考答案

一、选择题(每小题3分,共30分)

1、A

2、D

3、C

4、B

5、C

6、C

7、A

8、D

9、B

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、6＜v＜2或v＝4.2

13、1.

14、m＞1

15、13

16、40°

三、解下列各题(本大题共8小题，共72分)

17、见解析

18、 (1)；(2)；(3)见解析.

19、 (1) －＜m＜3；(1) 点P的坐标为（3，﹣1）或（﹣3，-5）

20、 (1)(，且为整数)；(2)当购买电子白板6台，台式电脑18台学校总费用最少钱，最少是108000元.

21、（1）16−6；（2）4；.

22、（1）甲班选手进球数的平均数为7，中位为7，众数为7；乙班选手进球数的平均数为7，中位为7，众数为7；（2）要争取夺取总进球团体第一名，应选乙班；要进入学校个人前3名，应选甲班．

23、（1）y＝－2x＋1；（2）2；点P的坐标为(0，1)．

24、（1）（2）；（3）