


2022-2023学年广东省深圳市翠园中学数学七下期末学业水平测试试题含答案
展开这是一份2022-2023学年广东省深圳市翠园中学数学七下期末学业水平测试试题含答案,共8页。
2022-2023学年广东省深圳市翠园中学数学七下期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
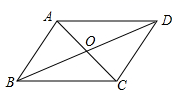
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
2.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对边平行 C.对角互补 D.内角和为360°
3.在矩形ABCD中,AB=3,BC=2![]() ,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
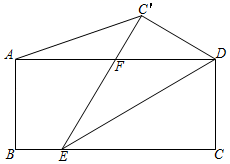
A.![]() B.2
B.2![]() C.2
C.2![]() D.
D.![]() +1
+1
4.若使二次根式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.对于正比例函数 y 3x ,下列说法正确的是( )
A.y 随 x 的增大而减小 B.y 随 x 的增大而增大
C.y 随 x 的减小而增大 D.y 有最小值
6.若x、y都是实数,且![]() ,则xy的值为
,则xy的值为![]()
![]()
A.0 B.![]() C.2 D.不能确定
C.2 D.不能确定
7.在直角坐标系中,点![]() 关于原点对称的点为
关于原点对称的点为![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
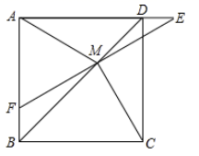
A.①②③ B.①②④ C.②③④ D.①②③④
9.如图是小明在物理实验课上用量筒和水测量铁块A的体积实验,小明在匀速向上将铁块提起,直至铁块完全露出水面一定高度的过程中,则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是( )
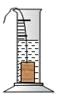
A.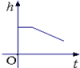 B.
B.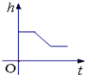 C.
C.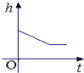 D.
D.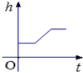
10.如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
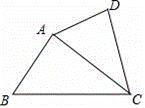
A.∠DAC=∠ABC B.AC是∠BCD的平分线 C.AC2=BC•CD D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
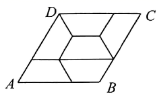
11.如图,菱形![]() 由6个腰长为2,且全等的等腰梯形镶嵌而成,则菱形的对角线
由6个腰长为2,且全等的等腰梯形镶嵌而成,则菱形的对角线![]() 的长为_____.
的长为_____.
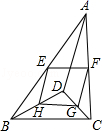
12.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .
13.在菱形ABCD中,对角线AC,BD的长分别是6和8,则菱形的周长是 .
14.如图,![]() 是
是![]() 内的一点,
内的一点,![]() ,点
,点![]() 分别在
分别在![]() 的两边上,
的两边上,![]() 周长的最小值是____.
周长的最小值是____.
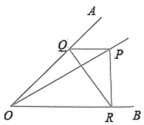
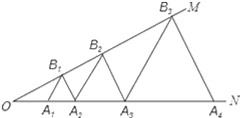
15.如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为______.
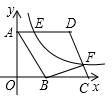
16.如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,且点A坐标为(0,4),BC在x轴正半轴上,点C在B点右侧,反比例函数![]() (x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE=
(x>0)的图象分别交边AD,CD于E,F,连结BF,已知,BC=k,AE=![]() CF,且S四边形ABFD=20,则k= _________.
CF,且S四边形ABFD=20,则k= _________.
三、解下列各题(本大题共8小题,共72分)
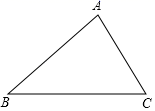
17.(8分)如图,已知△ABC.利用直尺和圆规,根据下列要求作图(不写作法,保留作图痕迹),并回答问题.
(1)作∠ABC的平分线BD、交AC于点D;
(2)作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE,DF;
(3)写出你所作出的图形中的相等线段.
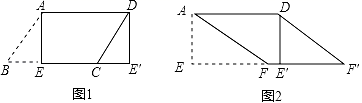
18.(8分)(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.
19.(8分)先化简,再求值:(1﹣![]() )÷
)÷![]() .其中a从0,1,2,﹣1中选取.
.其中a从0,1,2,﹣1中选取.
20.(8分)如图,在□ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
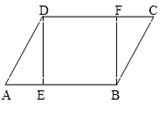
(1)求证:![]() ≌
≌![]() .
.
(2)若![]() DEB=90
DEB=90![]() ,求证四边形DEBF是矩形.
,求证四边形DEBF是矩形.
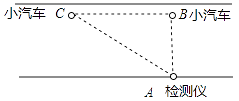
21.(8分) “中华人民共和国道路交通管理条例”规定:小汽车在高速公路上的行驶速度不得超过120千米/小时,不得低于60千米/小时,如图,一辆小汽车在高速公路上直道行驶,某一时刻刚好行驶到“车速检测点![]() ”正前方60米
”正前方60米![]() 处,过了3秒后,测得小汽车位置
处,过了3秒后,测得小汽车位置![]() 与“车速检测点
与“车速检测点![]() ”之间的距离为100米,这辆小汽车是按规定行驶吗?
”之间的距离为100米,这辆小汽车是按规定行驶吗?
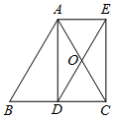
22.(10分)如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高.点
边上的高.点![]() 是
是![]() 中点,延长
中点,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)求四边形![]() 的面积.
的面积.
23.(10分)已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图(1),连接AF、CE.
①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

24.(12分)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
(1)直接写出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?

参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、A
4、A
5、B
6、C
7、B
8、A
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、1.
13、1.
14、![]()
15、32a
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)射线BD即为所求.见解析;(2)直线BD即为所求.见解析;(3)EB=ED=FD=FB,BO=DO,EO=FO.
18、(1)C;(2)详见解析.
19、![]() ,
,![]()
20、(1)利用SAS证明;(2)证明见解析.
21、这辆小汽车是按“中华人民共和国道路交通管理条例”规定行驶.̈
22、(1)见解析;(2)![]() .
.
23、(1) ①菱形,理由见解析;②AF=1;(2) ![]() 秒.
秒.
24、(1)![]() =
=![]() ,
,![]() =
=![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时
时![]() 是等腰三角形.
是等腰三角形.
相关试卷
这是一份广东省深圳市翠园初级中学2023-2024学年数学九上期末学业水平测试模拟试题含答案,共8页。
这是一份广东省深圳市翠园中学2023-2024学年数学八上期末监测试题含答案,共7页。
这是一份2022-2023学年第二附属中学数学七下期末学业水平测试模拟试题含答案,共6页。试卷主要包含了点关于轴对称的点的坐标是,若,,则代数式的值为等内容,欢迎下载使用。












