2022-2023学年广元市重点中学七下数学期末学业水平测试模拟试题含答案

2022-2023学年广元市重点中学七下数学期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．函数中自变量x的取值范围是（  ）

A．x≥ 1        B．x≤ 1         C．x≠ 1           D．x＞ 1

2．某学校为了了解九年级体能情况，随机选取30名学生测试一分钟仰卧起坐次数，并绘制了如图的直方图，学生仰卧起坐次数在25～30之间的频率为（　　）

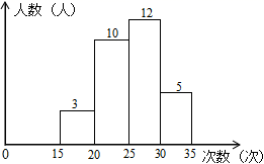
A．0.1 B．0.17 C．0.33 D．0.4

3．如图，已知△ABC，任取一点O，连AO，BO，CO，分别取点D，E，F，使OD＝AO，OE＝BO，OF＝CO，得△DEF，有下列说法：

①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；

③△DEF与△ABC的周长比为1：3；④△DEF与△ABC的面积比为1：1．

则正确的个数是（　　）

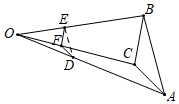
A．1 B．2 C．3 D．4

4．以下列各组线段为边，能构成直角三角形的是（　　）

A．1cm，2cm，3cm B． cm， cm，5cm C．6cm，8cm，10cm D．5cm，12cm，18cm

5．已知图2是由图1七巧板拼成的数字“0”，己知正方形ABCD的边长为4，则六边形EFGHMN的周长为（    ）

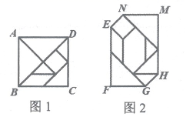
A． B． C． D．12

6．如图所示，DE是△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为（　　）

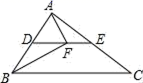
A． B．4 C． D．1

7．一个四边形，对于下列条件：①一组对边平行，一组对角相等；②一组对边平行，一条对角线被另一条对角线平分；③一组对边相等，一条对角线被另一条对角线平分；④两组对角的平分线分别平行，不能判定为平行四边形的是（     ）

A．① B．② C．③ D．④

8．下列计算不正确的是(   )

A． B． C． D．

9．要使分式有意义，则x的取值范围是（   ）

A．x>1 B．x≠1 C．x<1 D．x≠-1．

10．下列多项式中，分解因式不正确的是（　　）

A．a2+2ab=a（a+2b） B．a2-b2=（a+b）（a-b）

C．a2+b2=（a+b）2 D．4a2+4ab+b2=（2a+b）2

二、填空题(本大题共有6小题，每小题3分，共18分)

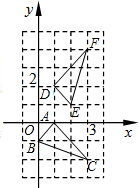
11．如图∆DEF是由∆ABC绕着某点旋转得到的，则这点的坐标是__________.

12．在一次“人与环境”知识竞赛中，共有25个题，每题四个答案，其中只有一个答案正确，每选对一题得4分，不选或选错倒扣2分，如果一个学生在本次竞赛中得分不低于60分，那么他至少要答对______题

13．方程的解是__________.

14．若反比例函数的图象经过点，则的图像在_______象限.

15．已知y是x的一次函数下表列出了部分对应值，则m=_______

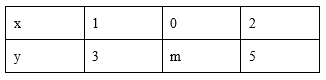
16．若y与x的函数关系式为y=2x-2，当x=2时，y的值为_______.

三、解下列各题(本大题共8小题，共72分)

17．（8分）因式分解：

（1）a（x﹣y）﹣b（y﹣x）2

（2）2x3﹣8x2+8x．

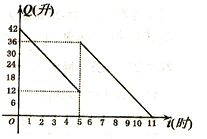
18．（8分）某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升；(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围；(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。

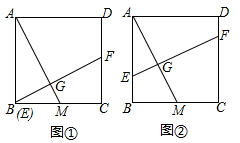
19．（8分）如图①，四边形是正方形，点是边的中点， ，且交正方形的外角平分线于点请你认真阅读下面关于这个图形的探究片段，完成所提出的问题.

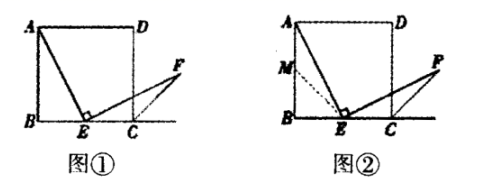
（1）探究1：小强看到图①后，很快发现这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（个直角三角形，一个钝角三角形）考虑到点E是边BC的中点，因此可以选取AB的中点M（如图②），连接EM后尝试着去证明就行了.随即小强写出了如下的证明过程：

证明：如图②，取AB的中点M，连接EM.

∵

∴

又∵

∴

∵点E、M分别为正方形的边BC和AB的中点，

∴

∴是等腰直角三角形，

∴

又∵是正方形外角的平分线，

∴，∴

∴

∴，

∴

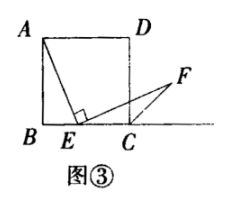
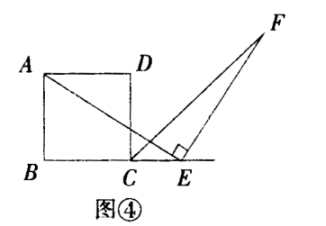
（2）探究2：小强继续探索，如图③，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立小强进一步还想试试，如图④，若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.

20．（8分）.解方程：

（1）            （2）

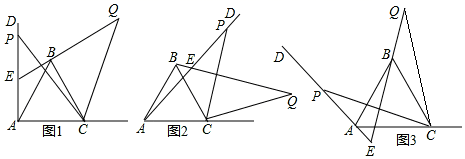
21．（8分）如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．

（1）如图1，猜想∠QEP=　   　°；

（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；

（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．

22．（10分）今年受疫情影响，我市中小学生全体在家线上学习．为了了解学生在家主动锻炼身体的情况，某校随机抽查了部分学生，对他们每天的运动时间进行调查，并将调查统计的结果分为四类：每天运动时间t≤20分钟的学生记为A类，20分钟＜t≤40分钟记为B类，40分钟＜t≤60分钟记为C类，t＞60分钟记为D类．收集的数据绘制如下两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

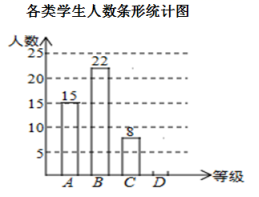
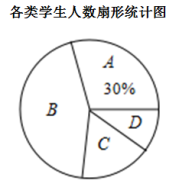
（1）这次共抽取了_________名学生进行调查统计；

（2）将条形统计图补充完整，扇形统计图中D类所对应的扇形圆心角大小为_________；

（3）如果该校共有3000名学生，请你估计该校B类学生约有多少人？

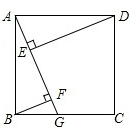
23．（10分）如图，正方形ABCD，AB=4，点M是边BC的中点，点E是边AB上的一个动点，作EG⊥AM交AM于点G，EG的延长线交线段CD于点F．

（1）如图①，当点E与点B重合时，求证：BM=CF；

（2）设BE=x，梯形AEFD的面积为y，求y与x的函数解析式，并写出定义域．

24．（12分）如图，四边形是正方形，点是边上的任意一点，于点，，且交于点，求证：

（1）

（2）

参考答案

一、选择题(每小题3分,共30分)

1、A

2、D

3、C

4、C

5、B

6、A

7、C

8、B

9、B

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、（0，1）．

12、19

13、

14、二、四

15、1

16、2

三、解下列各题(本大题共8小题，共72分)

17、（1）（x﹣y）[a﹣b（x﹣y）]；（1）1x（x﹣1）1．

18、（1）5，24；（2）Q=42-6t（0≤t≤5）；（3）够用，见解析.

19、见解析

20、（1），;（2），

21、（1）∠QEP=60°；（2）∠QEP=60°，证明详见解析；（3）

22、（1）50；（2）图见解析，；（3）该校B类学生约有1320人．

23、（1）见解析；（2）y与x的函数解析式为.

24、（1）见详解；（2）见详解.