


2022-2023学年江苏省淮安市实验初级中学数学七下期末调研试题含答案
展开
这是一份2022-2023学年江苏省淮安市实验初级中学数学七下期末调研试题含答案,共6页。试卷主要包含了下列命题是真命题的是等内容,欢迎下载使用。
2022-2023学年江苏省淮安市实验初级中学数学七下期末调研试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列式子:①y=3x﹣5;②y=![]() ;③y=
;③y=![]() ;④y2=x;⑤y=|x|,其中y是x的函数的个数是( )A.2个 B.3个 C.4个 D.5个2.如图,正方形ABCD的周长是16,P是对角线AC上的个动点,E是CD的中点,则PE+PD的最小值为( )
;④y2=x;⑤y=|x|,其中y是x的函数的个数是( )A.2个 B.3个 C.4个 D.5个2.如图,正方形ABCD的周长是16,P是对角线AC上的个动点,E是CD的中点,则PE+PD的最小值为( )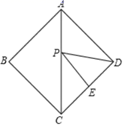 A.2
A.2![]() B.2
B.2![]() C.2
C.2![]() D.43.不等式5+2x <1的解集在数轴上表示正确的是( ).A.
D.43.不等式5+2x <1的解集在数轴上表示正确的是( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如果点
4.如果点![]() 在正比例函数
在正比例函数![]() 的图像上,那么下列等式一定成立的是( )A.
的图像上,那么下列等式一定成立的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
5.如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )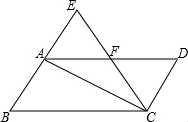 A.4个 B.3个 C.2个 D.1个6.下列命题是真命题的是( )A.对角线互相垂直且相等的四边形是正方形B.对角线相互平分的四边形是菱形C.对角线相互垂直的四边形是平行四边形D.对角线相等的平行四边形是矩形7.如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.4个 B.3个 C.2个 D.1个6.下列命题是真命题的是( )A.对角线互相垂直且相等的四边形是正方形B.对角线相互平分的四边形是菱形C.对角线相互垂直的四边形是平行四边形D.对角线相等的平行四边形是矩形7.如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( ) A.
A.![]() -1 B.
-1 B.![]() C.
C.![]() D.28.我县某贫围户2016年的家庭年收入为4000元,由于党的扶贫政策的落实,2017、2018年家庭年收入增加到共15000元,设平均每年的增长率为x,可得方程( )A.4000(1+x)2=15000 B.4000+4000(1+x)+4000(1+x)2=15000C.4000(1+x)+4000(1+x)2=15000 D.4000+4000(1+x)2=150009.如图,已知▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
D.28.我县某贫围户2016年的家庭年收入为4000元,由于党的扶贫政策的落实,2017、2018年家庭年收入增加到共15000元,设平均每年的增长率为x,可得方程( )A.4000(1+x)2=15000 B.4000+4000(1+x)+4000(1+x)2=15000C.4000(1+x)+4000(1+x)2=15000 D.4000+4000(1+x)2=150009.如图,已知▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )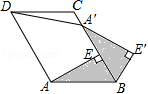 A.130° B.150° C.160° D.170°10.在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中54.5~57.5这一组的频数是6,那么它的频率为( )A.0.12 B.0.60 C.6 D.1211.下列四个图形是中心对称图形的是( )A.
A.130° B.150° C.160° D.170°10.在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中54.5~57.5这一组的频数是6,那么它的频率为( )A.0.12 B.0.60 C.6 D.1211.下列四个图形是中心对称图形的是( )A.  B.
B.  C.
C. 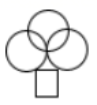 D.
D.  12.若
12.若![]() 有增根,则m的值是( )A.3 B.2 C.﹣3 D.﹣2二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数y=-6x+8的图象,可以看作由直线y=-6x向_____平移_____个单位长度而得到.14.已知直线
有增根,则m的值是( )A.3 B.2 C.﹣3 D.﹣2二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数y=-6x+8的图象,可以看作由直线y=-6x向_____平移_____个单位长度而得到.14.已知直线![]() 不经过第一象限,则
不经过第一象限,则![]() 的取值范围是_____________。15.已知一次函数
的取值范围是_____________。15.已知一次函数![]() 的图象经过点
的图象经过点![]() ,则不等式
,则不等式![]() 的解是__________.16.将直线
的解是__________.16.将直线![]() 向上平移1个单位,那么平移后所得直线的表达式是_______________17.将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 ______.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知m和n是两个两位数,把m和n中任意一个两位数的十位数字放置于另一个两位数的十位数字与个位数字之间,再把其个位数字放置于另一个两位数的个位数字的右边,就可以得到两个新四位数,把这两个新四位数的和除以11的商记为W(m,n).例如:当m=36,n=10时,将m十位上的3放置于n的1、0之间,将m个位上的6放置于n中0的右边,得到1306;将n十位上的1放置于m的3、6之间,将n个位上的0放置于m中6的右边,得到1.这两个新四位数的和为1306+1=4466,4466÷11=2,所以W(36,10)=2.(1)计算:W(20,18);(2)若a=10+x,b=10y+8(0≤x9,1≤y≤9,x,y都是自然数).①用含x的式子表示W(a,36);用含y的式子表示W(b,49);②当150W(a,36)+W(b,49)=62767时,求W(5a,b)的最大值. 19.(5分)如图①,在矩形ABCD中,AB=
向上平移1个单位,那么平移后所得直线的表达式是_______________17.将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 ______.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知m和n是两个两位数,把m和n中任意一个两位数的十位数字放置于另一个两位数的十位数字与个位数字之间,再把其个位数字放置于另一个两位数的个位数字的右边,就可以得到两个新四位数,把这两个新四位数的和除以11的商记为W(m,n).例如:当m=36,n=10时,将m十位上的3放置于n的1、0之间,将m个位上的6放置于n中0的右边,得到1306;将n十位上的1放置于m的3、6之间,将n个位上的0放置于m中6的右边,得到1.这两个新四位数的和为1306+1=4466,4466÷11=2,所以W(36,10)=2.(1)计算:W(20,18);(2)若a=10+x,b=10y+8(0≤x9,1≤y≤9,x,y都是自然数).①用含x的式子表示W(a,36);用含y的式子表示W(b,49);②当150W(a,36)+W(b,49)=62767时,求W(5a,b)的最大值. 19.(5分)如图①,在矩形ABCD中,AB=![]() ,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.(1)求△PEF的边长;(2)若△PEF的边EF在线段CB上移动,试猜想:PH与BE有何数量关系?并证明你猜想的结论;(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示,CF>1,P不与A重合),(2)中的结论还成立吗?若不成立,直接写出你发现的新结论.
,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.(1)求△PEF的边长;(2)若△PEF的边EF在线段CB上移动,试猜想:PH与BE有何数量关系?并证明你猜想的结论;(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示,CF>1,P不与A重合),(2)中的结论还成立吗?若不成立,直接写出你发现的新结论.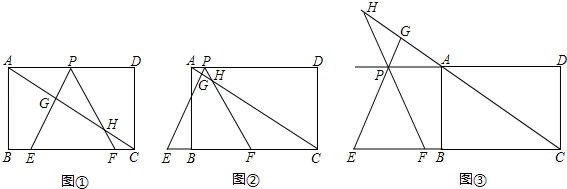 20.(8分)如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.(1)求证:△AFE≌△CDF;(2)若AB=4,BC=8,求图中阴影部分的面积.
20.(8分)如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.(1)求证:△AFE≌△CDF;(2)若AB=4,BC=8,求图中阴影部分的面积.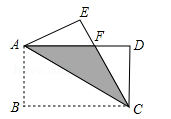 21.(10分)为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=
21.(10分)为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?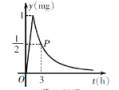 22.(10分)阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想
22.(10分)阅读材料:各类方程的解法求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;(2)拓展:用“转化”思想求方程
转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;(2)拓展:用“转化”思想求方程![]() 的解;(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
的解;(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.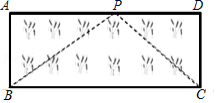 23.(12分)求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?
23.(12分)求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?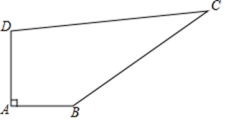 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、C4、D5、B6、D7、A8、C9、C10、A11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、上 1 14、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、C4、D5、B6、D7、A8、C9、C10、A11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、上 1 14、![]() 15、
15、![]() 16、
16、![]() 17、y=1x-1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)308;(2)① W(a,36)=[1+x+1306+10x)÷11;W(b,49)=(489+1000y+4098+100y)÷11;②W(5a,b)最大值为3.19、(1)△PEF的边长为2;(2)PH﹣BE=1,证明见解析;(3)结论不成立,当1<CF<2时,PH=1﹣BE,当2<CF<3时,PH=BE﹣1.20、(1)证明见解析;(2)1.21、 (1)y=
17、y=1x-1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)308;(2)① W(a,36)=[1+x+1306+10x)÷11;W(b,49)=(489+1000y+4098+100y)÷11;②W(5a,b)最大值为3.19、(1)△PEF的边长为2;(2)PH﹣BE=1,证明见解析;(3)结论不成立,当1<CF<2时,PH=1﹣BE,当2<CF<3时,PH=BE﹣1.20、(1)证明见解析;(2)1.21、 (1)y=![]() t(0≤t≤
t(0≤t≤![]() ) (2)6小时22、 (1)-2,1;(2)x=3;(3)4m.23、学校需要投入9000元资金买草皮.
) (2)6小时22、 (1)-2,1;(2)x=3;(3)4m.23、学校需要投入9000元资金买草皮.
相关试卷
这是一份2022-2023学年湖北省黄冈实验中学数学七下期末调研试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份2022-2023学年江苏省盐城市大丰区实验初级中学数学七下期末检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,在、、、、中,分式的个数是,下列变形错误的是,下列式子为最简二次根式的是等内容,欢迎下载使用。
这是一份2022-2023学年江苏省淮安市凌桥乡初级中学数学七下期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列式子从左到右变形错误的是,如图,点P,若x=1,则x的值是等内容,欢迎下载使用。








