


2022-2023学年江苏省泰州海陵学校七年级数学第二学期期末教学质量检测模拟试题含答案
展开
这是一份2022-2023学年江苏省泰州海陵学校七年级数学第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了分式方程-1=的解为等内容,欢迎下载使用。
2022-2023学年江苏省泰州海陵学校七年级数学第二学期期末教学质量检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列根式中是最简二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.下列是最简二次根式的为( )A.
2.下列是最简二次根式的为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() (a>0)3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为
(a>0)3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为![]() ,则所有正方形的面积的和是
,则所有正方形的面积的和是![]()
![]() .
.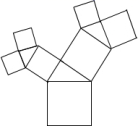 A.28 B.49 C.98 D.1474.已知关于
A.28 B.49 C.98 D.1474.已知关于![]() 的方程
的方程![]() 的两根互为倒数,则
的两根互为倒数,则![]() 的值为( )A.
的值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.下列图形中,既是轴对称图形,又是中心对称图形的是( )A.等边三角形 B.等腰直角三角形C.平行四边形 D.菱形6.如图,边长为2的菱形ABCD中,∠A=60º,点M是边AB上一点,点N是边BC上一点,且∠ADM=15º,∠MDN=90º,则点B到DN的距离为( )
5.下列图形中,既是轴对称图形,又是中心对称图形的是( )A.等边三角形 B.等腰直角三角形C.平行四边形 D.菱形6.如图,边长为2的菱形ABCD中,∠A=60º,点M是边AB上一点,点N是边BC上一点,且∠ADM=15º,∠MDN=90º,则点B到DN的距离为( )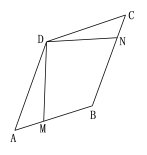 A.
A.![]() B.
B.![]() C.
C.![]() D.27.一次函数y=ax+b,b>0,且y随x的增大而减小,则其图象可能是( )A.
D.27.一次函数y=ax+b,b>0,且y随x的增大而减小,则其图象可能是( )A.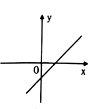 B.
B.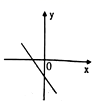 C.
C.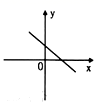 D.
D.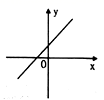 8.如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( )
8.如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( )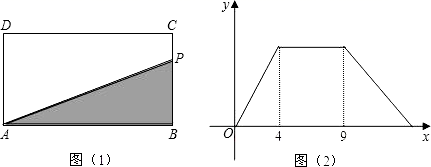 A.10 B.16 C.20 D.369.如图,已知
A.10 B.16 C.20 D.369.如图,已知![]() ,点D、E、F分别是
,点D、E、F分别是![]() 、
、![]() 、
、![]() 的中点,下列表示不正确的是()
的中点,下列表示不正确的是()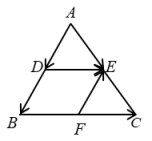 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.分式方程
10.分式方程![]() -1=
-1=![]() 的解为( )A.x=1 B.x=-1 C.无解 D.x=-211.矩形、菱形、正方形都具有的性质是( )A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线互相平分且相等12.下列各式从左到右的变形中,是因式分解的是( )A.
的解为( )A.x=1 B.x=-1 C.无解 D.x=-211.矩形、菱形、正方形都具有的性质是( )A.对角线相等 B.对角线互相平分 C.对角线互相垂直 D.对角线互相平分且相等12.下列各式从左到右的变形中,是因式分解的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数![]() 的自变量x的取值范围是______.14.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.
的自变量x的取值范围是______.14.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.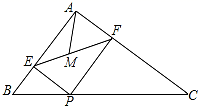 15.若一直角三角形的两边长为4、5,则第三边的长为________ .16.如图,矩形
15.若一直角三角形的两边长为4、5,则第三边的长为________ .16.如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 在数轴上,若以点
在数轴上,若以点![]() 为圆心,对角线
为圆心,对角线![]() 的长为半径作弧交数轴的正半轴于
的长为半径作弧交数轴的正半轴于![]() ,则点
,则点![]() 的表示的数为_____.
的表示的数为_____.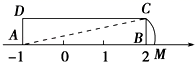 17.如果一组数据的方差为
17.如果一组数据的方差为![]() ,那么这组数据的标准差是________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图 1,在正方形 ABCD 中, P 是对角线 AC 上的一点,点 E 在 BC 的延长线上,且PE PB .(1)求证: △BCP≌△DCP ;(1)求证: DPE ABC ;(3)把正方形 ABCD 改为菱形 ABCD ,且 ABC 60 ,其他条件不变,如图 1.连接 DE , 试探究线段 BP 与线段 DE 的数量关系,并说明理由.
,那么这组数据的标准差是________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图 1,在正方形 ABCD 中, P 是对角线 AC 上的一点,点 E 在 BC 的延长线上,且PE PB .(1)求证: △BCP≌△DCP ;(1)求证: DPE ABC ;(3)把正方形 ABCD 改为菱形 ABCD ,且 ABC 60 ,其他条件不变,如图 1.连接 DE , 试探究线段 BP 与线段 DE 的数量关系,并说明理由.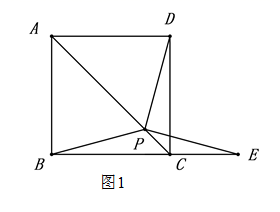
 19.(5分)先化简,再求值:
19.(5分)先化简,再求值:![]() ,其中
,其中![]() 的值从不等式组
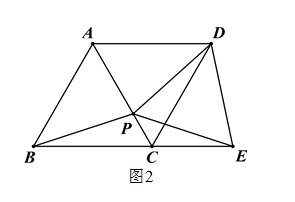
的值从不等式组![]() 的整数解中选取. 20.(8分)已知正方形
的整数解中选取. 20.(8分)已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.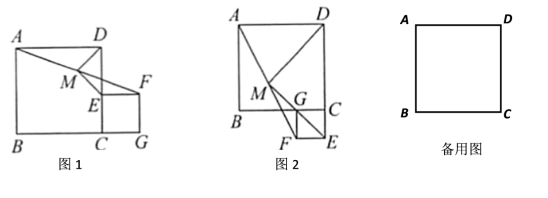 (1)如图1,点
(1)如图1,点![]() 在上,点在的延长线上, 求证:
在上,点在的延长线上, 求证:![]() =ME,
=ME,![]() ⊥.ME简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.(2)如图2, 在
⊥.ME简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= . 21.(10分)如图所示,每个小正方形的边长为1cm(1)求四边形ABCD的面积;(2)四边形ABCD中有直角吗?若有,请说明理由.
在直线CD上,则DM= ;若点E在直线BC上,则DM= . 21.(10分)如图所示,每个小正方形的边长为1cm(1)求四边形ABCD的面积;(2)四边形ABCD中有直角吗?若有,请说明理由.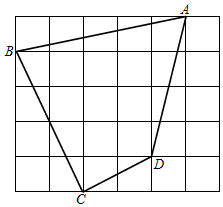 22.(10分)如图,在平面直角坐标系中,△ABC的顶点A、B分别落在x轴、y轴的正半轴上,顶点C在第一象限,BC与x轴平行.已知BC=2,△ABC的面积为1.(1)求点C的坐标.(2)将△ABC绕点C顺时针旋转90°,△ABC旋转到△A1B1C的位置,求经过点B1的反比例函数关系式.
22.(10分)如图,在平面直角坐标系中,△ABC的顶点A、B分别落在x轴、y轴的正半轴上,顶点C在第一象限,BC与x轴平行.已知BC=2,△ABC的面积为1.(1)求点C的坐标.(2)将△ABC绕点C顺时针旋转90°,△ABC旋转到△A1B1C的位置,求经过点B1的反比例函数关系式.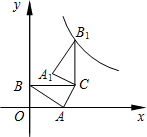 23.(12分)随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如右表格(部分信息未给出):根据以上信息解答下列问题:选项频数频率A10
23.(12分)随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如右表格(部分信息未给出):根据以上信息解答下列问题:选项频数频率A10![]() B
B![]() 0.2C50.1D
0.2C50.1D![]() 0.4E50.1(1)这次被调查的学生有多少人?(2)求表中
0.4E50.1(1)这次被调查的学生有多少人?(2)求表中![]() ,
,![]() 的值;(3)若该中学有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、A3、D4、C5、D6、B7、C8、C9、A10、C11、B12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、:x≠﹣1.14、1.215、
的值;(3)若该中学有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、A3、D4、C5、D6、B7、C8、C9、A10、C11、B12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、:x≠﹣1.14、1.215、![]() 或116、
或116、![]() 17、
17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(1)见解析;(3)BP=DE,理由见解析.19、-2.20、(1)等腰直角;(2)结论仍成立,见解析;(3)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(1)见解析;(3)BP=DE,理由见解析.19、-2.20、(1)等腰直角;(2)结论仍成立,见解析;(3)![]() 或
或![]() ,
,![]() .21、(1)14
.21、(1)14![]() ;(2)四边形ABCD中有直角.22、(1)C(2,1);(2)经过点B1的反比例函数为y=
;(2)四边形ABCD中有直角.22、(1)C(2,1);(2)经过点B1的反比例函数为y=![]() .23、(1)50人;(2)0.2、10;(3)400人
.23、(1)50人;(2)0.2、10;(3)400人
相关试卷
这是一份江苏省泰州市海陵2023-2024学年九上数学期末复习检测试题含答案,共10页。试卷主要包含了设A等内容,欢迎下载使用。
这是一份2023-2024学年江苏省泰州海陵学校数学九上期末学业水平测试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,设A等内容,欢迎下载使用。
这是一份江苏省泰州市海陵2023-2024学年八上数学期末学业水平测试模拟试题含答案,共7页。试卷主要包含了下列说法正确的是等内容,欢迎下载使用。








