


2022-2023学年江苏省金湖县七下数学期末质量跟踪监视模拟试题含答案
展开2022-2023学年江苏省金湖县七下数学期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.分式方程![]() 的解为( )
的解为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在平行四边形ABCD中,数据如图,则∠D的度数为( )
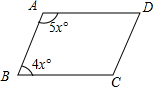
A.20° B.80° C.100° D.120°
3.下列不等式的变形中,不正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
4.随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
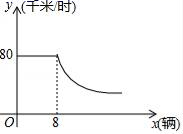
A.x<32 B.x≤32 C.x>32 D.x≥32
5.如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
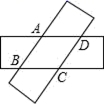
A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BC
C.AB=CD,AD=BC D.∠DAB+∠BCD=180°
6.寓言故事《乌鸦喝水》教导我们遇到困难要运用智慧、认真思考才能让问题迎刃而解.如图,一个紧口瓶中盛有一些水,可乌鸦的嘴够不到瓶中的水.于是乌鸦衔来一些小石子放入瓶中,瓶中的水面高度得到提升.由于放入的石子较多,水都快溢出来了,乌鸦成功喝到了水,如果衔入瓶中石子的体积为![]() ,水面高度为
,水面高度为![]() ,下面图象能大致表示该故事情节的是( )
,下面图象能大致表示该故事情节的是( )
A.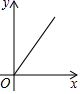 B.
B.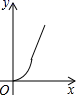 C.
C.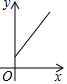 D.
D.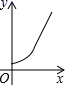
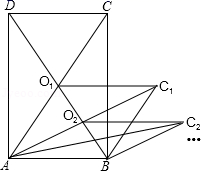
7.如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
A.![]() B.5×
B.5×![]() C.5×
C.5×![]() D.5×
D.5×![]()
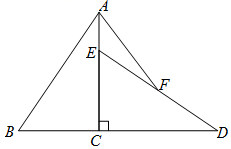
8.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )
A.4 B.5 C.![]() D.6
D.6
9.已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根
有两个实数根![]() ,
,![]() .则代数式
.则代数式![]() 的值为( )
的值为( )
A.10 B.2 C.![]() D.
D.![]()
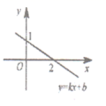
10.一次函数![]() 是(
是(![]() 是常数,
是常数,![]() )的图像如图所示,则不等式
)的图像如图所示,则不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
| 甲 | 乙 | 丙 | 丁 |
平均数/环 |
|
|
|
|
方差/环 |
|
|
|
|
请你根据表中数据选一人参加比赛,最合适的人选是( )
A.甲 B.乙 C.丙 D.丁
12.下列计算正确的是( )
A.m6•m2=m12 B.m6÷m2=m3
C.(![]() )5=
)5=![]() D.(m2)3=m6
D.(m2)3=m6
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.▱ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,则△OBC的周长是_____cm.
14.一个n边形的内角和是720°,则n=_____.
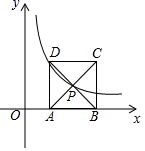
15.如图,正方形ABCD的顶点A,B在x轴的正半轴上,对角线AC,BD交于点P,反比例函数![]() 的图象经过P,D两点,则AB的长是______.
的图象经过P,D两点,则AB的长是______.
16.在矩形ABCD中,∠BAD的角平分线交于BC点E,且将BC分成1:3的两部分,若AB=2,那么BC=______
17.如图,已知A点的坐标为![]() ,直线
,直线![]() 与y轴交于点B,连接AB,若
与y轴交于点B,连接AB,若![]() ,则
,则![]() ____________.
____________.
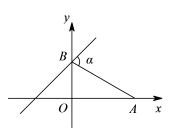
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
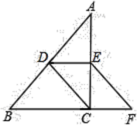
18.(5分)如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)证明:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 的周长是
的周长是![]() ,
,![]() 的长为
的长为![]() ,求线段
,求线段![]() 的长度.
的长度.
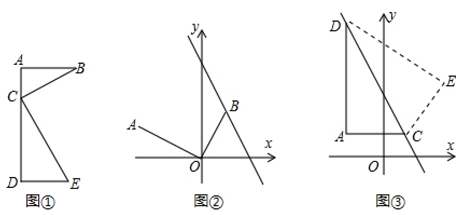
19.(5分)探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,![]() 字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
![]() .
.
(1)请就图①证明上述“模块”的合理性;
(2)请直接利用上述“模块”的结论解决下面两个问题:
①如图②,已知点![]() ,点
,点![]() 在直线
在直线![]() 上运动,若
上运动,若![]() ,求此时点
,求此时点![]() 的坐标;
的坐标;
②如图③,过点![]() 作
作![]() 轴与
轴与![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,求点
,求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标.
的坐标.
20.(8分)某县为了了解2018年初中毕业生毕业后的去向,对部分九年级学生进行了抽样调查,就九年级学生的四种去向(A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他)进行数据统计,并绘制了两幅不完整的统计图(如图①②)请问:
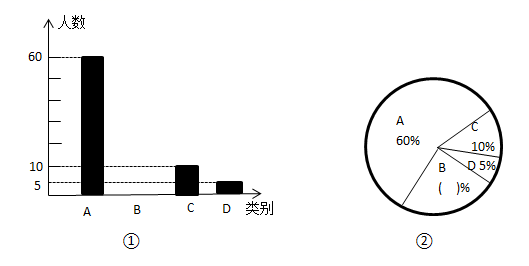
(1)本次共调查了_ 名初中毕业生;
(2)请计算出本次抽样调查中,读职业高中的人数和所占百分比,并将两幅统计图中不完整的部分补充完整;
(3)若该县2018年九年级毕业生共有![]() 人,请估计该县今年九年级毕业生读职业高中的学生人数.
人,请估计该县今年九年级毕业生读职业高中的学生人数.
21.(10分)某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类 | (A)学生夜场票 | (B)学生日通票 | (C)节假日通票 |
单价(元) | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,C种票y张.
(1)直接写出y与x之间的函数关系式;
(2)设购票总费用为w元,求w(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.
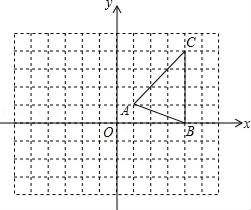
22.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A1B1C1.
(1)求点C1在旋转过程中所经过的路径长.
23.(12分)某直销公司现有![]() 名推销员,
名推销员,![]() 月份每个人完成销售额(单位:万元),数据如下:
月份每个人完成销售额(单位:万元),数据如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面的数据得到如下统计表:
销售额 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)统计表中的![]() ;
;![]() ;
;
(2)销售额的平均数是 ;众数是 ;中位数是 .
(3)![]() 月起,公司为了提高推销员的积极性,将采取绩效工资制度:规定一个基本销售额,在基本销售额内,按
月起,公司为了提高推销员的积极性,将采取绩效工资制度:规定一个基本销售额,在基本销售额内,按![]() 抽成;从公司低成本与员工愿意接受两个层面考虑,你认为基本销售额定位多少万元?请说明理由.
抽成;从公司低成本与员工愿意接受两个层面考虑,你认为基本销售额定位多少万元?请说明理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、B
3、D
4、B
5、D
6、D
7、C
8、B
9、B
10、C
11、A
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1.
14、1
15、2
16、8或![]()
17、2
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)见解析;(2)![]() .
.
19、(1)见解析;(2)①![]() ;②
;②![]()
20、(1)100;(2)25%,画图见解析;(3)2500人.
21、(1)y=93-4x;(2)w=-160x+14790;(3) 共有3种购票方案, 当A种票为22张,B种票73张,C种票为5张时费用最少,最少费用为11270元.
22、(1)①见解析;②见解析;(1)1π.
23、(1)![]() ,
,![]() ;(2)平均数:
;(2)平均数:![]() ,众数:
,众数:![]() ,中位数:
,中位数:![]() ;(3)基本销售额定为
;(3)基本销售额定为![]() 万元,理由详见解析.
万元,理由详见解析.
江苏省盱眙县2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省盱眙县2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了小勇投标训练4次的成绩分别是,下列函数中,是的正比例函数的是,用配方法解方程,则方程可变形为,如果方程有增根,那么k的值等内容,欢迎下载使用。
江苏省徐州市泉山区2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省徐州市泉山区2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了一元二次方程x等内容,欢迎下载使用。
江苏省常州市新北区2022-2023学年七下数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省常州市新北区2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。












