


2022-2023学年江西省安远县三百山中学七下数学期末质量跟踪监视试题含答案
展开
这是一份2022-2023学年江西省安远县三百山中学七下数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了如图在5×5的正方形网格中等内容,欢迎下载使用。
2022-2023学年江西省安远县三百山中学七下数学期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.函数![]() 的图像经过一、二、四象限,则
的图像经过一、二、四象限,则![]() 的取值范围是
的取值范围是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计.下列表示我国古代窗棂样式结构图案中,既是中心对称图形又是轴对称图形的是( )A.
2.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计.下列表示我国古代窗棂样式结构图案中,既是中心对称图形又是轴对称图形的是( )A.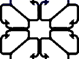 B.
B.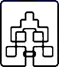 C.
C. D.
D. 3.某班主任老师为了对学生乱花钱的现象进行教育指导,对班里每位同学一周内大约花钱数额进行了统计,如下表:学生花钱数(元)
3.某班主任老师为了对学生乱花钱的现象进行教育指导,对班里每位同学一周内大约花钱数额进行了统计,如下表:学生花钱数(元)
5
10
15
20
25
学生人数
7
12
18
10
3
根据这个统计表可知,该班学生一周花钱数额的众数、平均数是( )A.15,14 B.18,14 C.25,12 D.15,124.生物学家发现:生物具有遗传多样性,遗传密码大多储存在![]() 分子上.一个
分子上.一个![]() 分子的直径约为0.0000002
分子的直径约为0.0000002![]() ,这个数用科学计数法可以表示为( )A.
,这个数用科学计数法可以表示为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
5.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )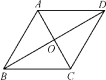 A.16
A.16![]() B.16 C.8
B.16 C.8![]() D.86.如图在5×5的正方形网格中(每个小正方形的边长为1个单位长度),格点上有A、B、C、E五个点,若要求连接两个点所成线段的长度大于3且小于4,则可以连接( )
D.86.如图在5×5的正方形网格中(每个小正方形的边长为1个单位长度),格点上有A、B、C、E五个点,若要求连接两个点所成线段的长度大于3且小于4,则可以连接( )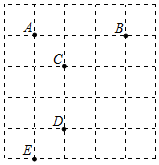 A.AE B.AB C.AD D.BE7.下列四组线段中,可以组成直角三角形的是( )A.4,5,6 B.3,4,5 C.5,6,7 D.1,
A.AE B.AB C.AD D.BE7.下列四组线段中,可以组成直角三角形的是( )A.4,5,6 B.3,4,5 C.5,6,7 D.1,![]() ,38.如图,一次函数
,38.如图,一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),过点
重合),过点![]() 分别作
分别作![]() 和
和![]() 的垂线,垂足为
的垂线,垂足为![]() .当矩形
.当矩形![]() 的面积为1时,点
的面积为1时,点![]() 的坐标为( )
的坐标为( )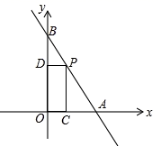 A.
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]() 9.如图,已知正比例函数
9.如图,已知正比例函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() .下面四个结论中正确的是( )
.下面四个结论中正确的是( )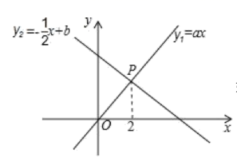 A.
A.![]() B.
B.![]() C.当
C.当![]() 时,
时,![]() D.当
D.当![]() 时,
时,![]() 10.函数y=mx+n与y=nx的大致图象是( )A.
10.函数y=mx+n与y=nx的大致图象是( )A.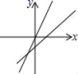 B.
B.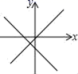 C.
C.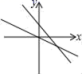 D.
D.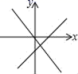 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.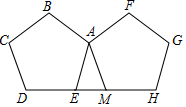 12.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.
12.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.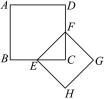 13.如图,四边形ABCD是梯形,AD∥BC,AC=BD,且AC⊥BD,如果梯形ABCD的中位线长是5,那么这个梯形的高AH=___.
13.如图,四边形ABCD是梯形,AD∥BC,AC=BD,且AC⊥BD,如果梯形ABCD的中位线长是5,那么这个梯形的高AH=___.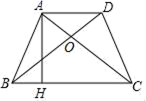 14.一种运算:规则是x※y=
14.一种运算:规则是x※y=![]() -
-![]() ,根据此规则化简(m+1)※(m-1)的结果为_____.15.如图,已知
,根据此规则化简(m+1)※(m-1)的结果为_____.15.如图,已知![]() ,点
,点![]() 是等腰
是等腰![]() 斜边
斜边![]() 上的一动点,以
上的一动点,以![]() 为一边向右下方作正方形
为一边向右下方作正方形![]() ,当动点
,当动点![]() 由点
由点![]() 运动到点
运动到点![]() 时,则动点
时,则动点![]() 运动的路径长为______.
运动的路径长为______.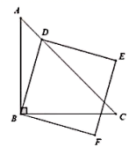 16.一次函数
16.一次函数![]() 的图像经过点
的图像经过点![]() ,且
,且![]() 的值随
的值随![]() 值的増大而增大,请你写出一个符合所有条件的点
值的増大而增大,请你写出一个符合所有条件的点![]() 的坐标__________.三、解下列各题(本大题共8小题,共72分)17.(8分)已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4=1.(1)当t=3时,解这个方程;(2)若m,n是方程的两个实数根,设Q=(m﹣2)(n﹣2),试求Q的最小值. 18.(8分)已知:如图,在菱形ABCD中,AC、BD交于点O,菱形的周长为8,∠ABC=60°,求BD的长和菱形ABCD的面积.
的坐标__________.三、解下列各题(本大题共8小题,共72分)17.(8分)已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4=1.(1)当t=3时,解这个方程;(2)若m,n是方程的两个实数根,设Q=(m﹣2)(n﹣2),试求Q的最小值. 18.(8分)已知:如图,在菱形ABCD中,AC、BD交于点O,菱形的周长为8,∠ABC=60°,求BD的长和菱形ABCD的面积.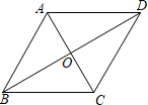 19.(8分)如图,直线
19.(8分)如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .(1)求
.(1)求![]() ,
,![]() 的值;(2)根据图像直接写出
的值;(2)根据图像直接写出![]() 时
时![]() 的取值范围;(3)垂直于
的取值范围;(3)垂直于![]() 轴的直线
轴的直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,若线段
,若线段![]() 长为2,求
长为2,求![]() 的值.
的值.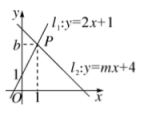 20.(8分)某校八年级甲,乙两班各有
20.(8分)某校八年级甲,乙两班各有![]() 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取
名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取![]() 名学生进行身体素质测试,测试成绩如下:甲班
名学生进行身体素质测试,测试成绩如下:甲班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 乙班
乙班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 整理上面数据,得到如下统计表:
整理上面数据,得到如下统计表: 样本数据的平均数、众数.中位数如下表所示:
样本数据的平均数、众数.中位数如下表所示: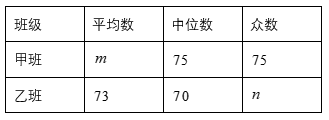 根据以上信息,解答下列问题:(1)求表中
根据以上信息,解答下列问题:(1)求表中![]() 的值(2)表中
的值(2)表中![]() 的值为( )(3)若规定测试成绩在
的值为( )(3)若规定测试成绩在![]() 分以上(含
分以上(含![]() 分)的学生身体素质为优秀,请估计乙班
分)的学生身体素质为优秀,请估计乙班![]() 名学生中身体素质为优秀的学生的人数. 21.(8分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.
名学生中身体素质为优秀的学生的人数. 21.(8分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.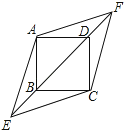 22.(10分)
22.(10分)![]() 中,
中,![]() 分别是
分别是![]() 上的不动点.且
上的不动点.且![]() ,点
,点![]() 是
是![]() 上的一动点.(1)当
上的一动点.(1)当![]() 时(如图1),求
时(如图1),求![]() 的度数;(2)若
的度数;(2)若![]() 时(如图2),求
时(如图2),求![]() 的度数还会与(1)的结果相同吗?若相同,请写出求解过程;若不相同,请说明理由.
的度数还会与(1)的结果相同吗?若相同,请写出求解过程;若不相同,请说明理由.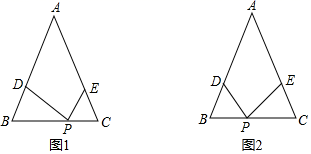 23.(10分)学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表: 选手表达能力阅读理解综合素质汉字听写甲85788573乙73808283(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们20%、10%、30%和40%的权重,请分别计算两名选手的最终成绩,从他们的这一成绩看,应选派谁. 24.(12分)如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时12海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去,2小时后,两船同时到达了目的地.若C、B两岛的距离为30海里,问乙船的航速是多少?
23.(10分)学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如下表: 选手表达能力阅读理解综合素质汉字听写甲85788573乙73808283(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们20%、10%、30%和40%的权重,请分别计算两名选手的最终成绩,从他们的这一成绩看,应选派谁. 24.(12分)如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时12海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去,2小时后,两船同时到达了目的地.若C、B两岛的距离为30海里,问乙船的航速是多少?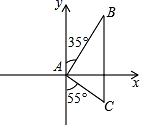 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、A4、B5、C6、C7、B8、C9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、144°.12、2
参考答案 一、选择题(每小题3分,共30分)1、C2、A3、A4、B5、C6、C7、B8、C9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、144°.12、2![]() 13、1.14、
13、1.14、![]() 15、
15、![]() 16、(1,2)(答案不唯一). 三、解下列各题(本大题共8小题,共72分)17、(2)x2=3﹣
16、(1,2)(答案不唯一). 三、解下列各题(本大题共8小题,共72分)17、(2)x2=3﹣![]() ,x2=3+
,x2=3+![]() ;(2)Q的最小值是﹣2.18、BD=2
;(2)Q的最小值是﹣2.18、BD=2![]() ,S菱形ABCD=2
,S菱形ABCD=2![]() .19、(1)
.19、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 20、(1)72;(2)70;(3)20.21、(1)证明见解析(2)菱形22、(1)
20、(1)72;(2)70;(3)20.21、(1)证明见解析(2)菱形22、(1)![]() ;(2)相同,
;(2)相同,![]() .23、(1)乙的平均成绩是79.5(分),应选派甲;(2)甲的最终成绩:79.5(分),乙的最终成绩:80.4(分),应选派乙.24、乙船的航速是 9海里/时.
.23、(1)乙的平均成绩是79.5(分),应选派甲;(2)甲的最终成绩:79.5(分),乙的最终成绩:80.4(分),应选派乙.24、乙船的航速是 9海里/时.
相关试卷
这是一份江西省安远县三百山中学2023-2024学年九上数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了两三角形的相似比是2,已知等内容,欢迎下载使用。
这是一份2023-2024学年江西省安远县三百山中学数学八上期末考试模拟试题含答案,共7页。试卷主要包含了下列各式,如图,是线段上的两点,,若分式的值为,则的值为,的绝对值是等内容,欢迎下载使用。
这是一份湖南省益阳市赫山区赫山万源中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了已知点,要使式子有意义,则x的值可以是等内容,欢迎下载使用。









