2022-2023学年江西省赣州市石城县七年级数学第二学期期末质量跟踪监视模拟试题含答案

2022-2023学年江西省赣州市石城县七年级数学第二学期期末质量跟踪监视模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题(每小题3分,共30分)

1．如图是一个直角三角形，它的未知边的长x等于　　

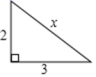
A．13 B． C．5 D．

2．计算的结果是（   ）

A． B． C． D．

3．计算的结果是(   )

A． B． C． D．

4．证明：平行四边形对角线互相平分．

已知：四边形ABCD是平行四边形，如图所示．

求证：，

以下是排乱的证明过程，正确的顺序应是

①，．②四边形ABCD是平行四边形．③，．④．⑤，（    ）

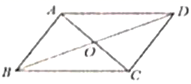
A．②①③④⑤ B．②③⑤①④ C．②③①④⑤ D．③②①④⑤

5．某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

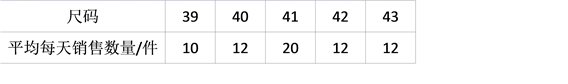
该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（　　）

A．平均数    B．方差    C．众数    D．中位数

6．对于分式方程，有以下说法：①最简公分母为（x﹣3）2；  ②转化为整式方程x＝2+3，解得x＝5；  ③原方程的解为x＝3；  ④原方程无解．其中，正确说法的个数为（　　）

A．1个 B．2个 C．3个 D．4个

7．下面四个图形中，不是轴对称图形的是(   )

A．                         B．                         C．                         D．

8．一次函数y＝kx+b中，y随x的增大而增大，b＜0，则这个函数的图象不经过(　　)

A．第一象限 B．第二象限 C．第三象限 D．第四象限

9．正方形ABCD内有一点E，且△ABE为等边三角形，则∠DCE为（  ）

A．15° B．18° C．1．5° D．30°

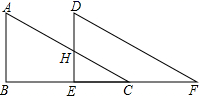
10．如图，沿直线边BC所在的直线向右平移得到，下列结论中不一定正确的是　　

A． B．

C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若直角三角形两边的长分别为a、b且满足+|b-4|=0，则第三边的长是 _________．

12．某招聘考试分笔试和面试两种，其中笔试按60%、面试按40%计算加权平均数，作为总成绩．孔明笔试成绩90分，面试成绩85分，那么孔明的总成绩是　   　分．

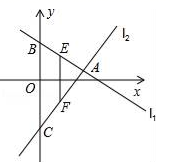
13．如图，已知直线l1：y=k1x+4与直线l2：y=k2x﹣5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB、AC的中点，则线段EF的长度为______．

14．化简：______.

15．若一元二次方程的两个实数根分别是、，则一次函数的图象一定不经过第____________象限.

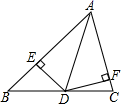
16．如图，在△ABC中，∠BAC=60°，点D在BC上，AD=10，DE⊥AB，DF⊥AC，垂足分别为E，F，且DE=DF，则DE的长为______．

三、解下列各题(本大题共8小题，共72分)

17．（8分）如果一个多位自然数的任意两个相邻数位上，右边数位上的数总比左边数位上的数大1，则我们称这样的自然数叫“美数”，例如：123，3456，67，…都是“美数”．

（1）若某个三位“美数”恰好等于其个位的76倍，这个“美数”为　   　．

（2）证明：任意一个四位“美数”减去任意一个两位“美数”之差再减去1得到的结果定能被11整除；

（3）如果一个多位自然数的任意两个相邻数位上，左边数位上的数总比右边数位上的数大1，则我们称这样的自然数叫“妙数”，若任意一个十位为为整数）的两位“妙数”和任意一个个位为为整数）的两位“美数”之和为55，则称两位数为“美妙数”，并把这个“美妙数”记为，则求的最大值．

18．（8分）如图，在平行四边形中，点，分别在边，的延长线上，且，分别与，交于点，．

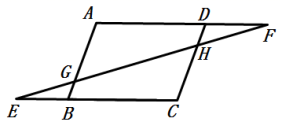
求证：．

19．（8分）解不等式组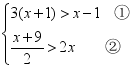，并将解集在数轴上表示出来．

20．（8分）某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：

（1）写出这15人该月加工零件数的平均数、中位数和众数．

（2）若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额，你认为这个定额是否合理，为什么？

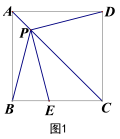
21．（8分）已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在BC边所在直线上， PE＝PB．

(1)如图1，当点E在线段BC上时，

求证：①PE＝PD，②PE⊥PD．

简析： 由正方形的性质，图1中有三对全等的三角形，

即△ABC≌△ADC，_______≌_______，和_______≌______，由全等三角形性质，结合条件中PE＝PB，易证PE＝PD．要证PE⊥PD，考虑到∠ECD = 90°，故在四边形PECD中，只需证∠PDC +∠PEC＝______即可.再结合全等三角形和等腰三角形PBE的性质，结论可证.

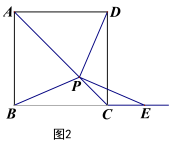
(2)如图2，当点E在线段BC的延长线上时，(1)中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由；

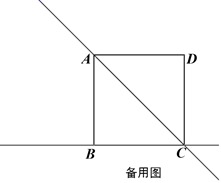
(3)若AB＝1，当△PBE是等边三角形时，请直接写出PB的长.

22．（10分） (1)解方程：﹣＝1

(2)先化简，再求值：÷(﹣x﹣2)，其中x＝﹣2

23．（10分）某乳品公司向某地运输一批牛奶，由铁路运输每千克需运费0.60元，由公路运输，每千克需运费0.30元，另需补助600元

（1）设该公司运输的这批牛奶为x千克，选择铁路运输时，所需运费为y1元，选择公路运输时，所需运费为y2元，请分别写出y1、y2与x之间的关系式；

（2）若公司只支出运费1500元，则选用哪种运输方式运送的牛奶多？若公司运送1500千克牛奶，则选用哪种运输方式所需费用较少？

24．（12分）在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

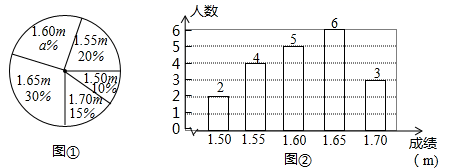
（1）图①中的值为______；

（2）求统计的这组初赛成绩数据的平均数、众数和中位数.

参考答案

一、选择题(每小题3分,共30分)

1、B

2、A

3、A

4、C

5、C

6、A

7、C

8、B

9、A

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、2或

12、88

13、．

14、

15、四

16、1

三、解下列各题(本大题共8小题，共72分)

17、 (1)456 （2）见解析 （3）42

18、见详解

19、，数轴表示见解析

20、（1）平均数：260件；中位数：240件；众数：240件（2）不合理，定额为240较为合理

21、 (1)△PAB；△PAD；△PBC；△PDC，180°；(2)成立，证明见解析；(3)或.

22、 (1)x＝2；(2)；-2.

23、（1）；（2）公路运输方式运送的牛奶多，铁路运输方式所需用较少．

24、（1）25；（2）平均数为：，众数为：，中位数为 .