2022-2023学年河南省罗山县七年级数学第二学期期末调研试题含答案

这是一份2022-2023学年河南省罗山县七年级数学第二学期期末调研试题含答案，共7页。试卷主要包含了如图，在中，，则的长为等内容，欢迎下载使用。
2022-2023学年河南省罗山县七年级数学第二学期期末调研试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．若一组数据，0，2，4，的极差为7，则的值是(    ).A． B．6 C．7 D．6或2．已知A（x1，y1），B（x2，y2）是一次函数y＝（2a﹣1）x﹣3图象上的两点，当x1＜x2时，有y1＞y2，则a的取值范围是（　　）A．a＜2 B．a＞ C．a＞2 D．a＜3．某楼盘2016年房价为每平方米15600元，经过两年连续降价后，2018年房价为每平方米12400元。设该楼盘这两年房价每年平均降低率为x，根据题意可列方程为（      ）A．15600(1-2x)=12400 B．2×15600(1-2x)=12400C．15600(1-x)2=12400 D．15600(1-x2)=124004．下列方程中，属于一元二次方程的是（    ）A． B． C． D．5．如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AC＝12km，BC＝16km，则M，C两点之间的距离为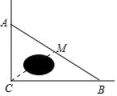（　　）A．13km B．12km C．11km D．10km6．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝8，DH＝3，平移距离为4，求阴影部分的面积为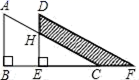（　　）A．20 B．24 C．25 D．267．为了比较某校同学汉字听写谁更优秀，语文老师随机抽取了8次听写情况，发现甲乙两人平均成绩一样，甲、乙的方差分别为1.9和2.3，则下列说法正确的是（　　）A．甲的发挥更稳定 B．乙的发挥更稳定C．甲、乙同学一样稳定 D．无法确定甲、乙谁更稳定8．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD+PE的和最小值为(　　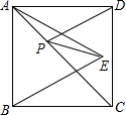)A． B．4 C．3 D．9．湖州是“两山”理论的发源地，在一次学校组织的以“学习两山理论，建设生态文明”为主题的知识竞赛中，某班6名同学的成绩如下（单位：分）：97,99,95,92,92,93，则这6名同学的成绩的中位数和众数分别为（   ）A．93分，92分 B．94分，92分C．94分，93分 D．95分，95分10．如图，在中，，则的长为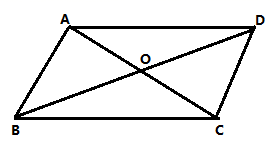（    ）A．2 B．4 C．6 D．811．若关于的方程产生增根，则的值是（    ）A． B． C．或 D．12．下列从左边到右边的变形，是因式分解的是（　　）A．y2﹣2y+4＝（y﹣2）2B．10x2﹣5x＝5x（2x﹣1）C．a（x+y）＝ax+ayD．t2﹣16+3t＝（t+4）（t﹣4）+3t二、填空题（每题4分，满分20分，将答案填在答题纸上）13．已知x、y为直角三角形两边的长，满足，则第三边的长为________.14．某航空公司规定，乘客所携带行李的重量x（kg）与运费y（元）满足如图所示的函数图象，那么每位乘客最多可免费携带____kg的行李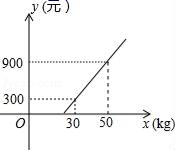．15．已知点P(-2,1)，则点P关于x轴对称的点的坐标是__．16．分解因式： =___________________.17．如果的值为负数，则 x 的取值范围是_____________．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商．经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元．经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费．另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人．（1）分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式；（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由．   19．（5分）如图，边长为 7 的正方形 OABC 放置在平面直角坐标系中，动点 P 从点 C 出发，以 每秒 1 个单位的速度向 O 运动，点 Q 从点 O 同时出发，以每秒 1 个单位的速度向点 A 运动，到达端点即停止运动，运动时间为 t 秒，连 PQ、BP、BQ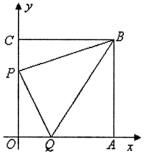．（1）写出 B 点的坐标；（2）填写下表：时间 t（单位：秒）123456OP 的长度      OQ 的长度      PQ 的长度      四边形 OPBQ 的面积      ①根据你所填数据，请描述线段 PQ 的长度的变化规律？并猜测 PQ 长度的最小值．②根据你所填数据，请问四边形 OPBQ 的面积是否会发生变化？并证明你的论断；（3）设点 M、N 分别是 BP、BQ 的中点，写出点 M，N 的坐标，是否存在经过 M， N 两点的反比例函数？如果存在，求出 t 的值；如果不存在，说明理由．   20．（8分）为了解某校九年级学生的理化实验操作情况，随机抽查了40名同学实验操作的得分．根据获取的样本数据，制作了如下的条形统计图和扇形统计图．请根据相关信息，解答下列问题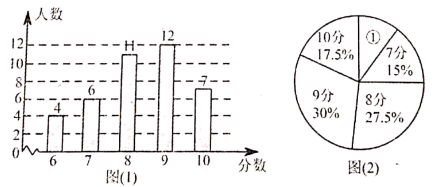．（1）①中的描述应为“ 6分m% ”，其中的m值为_________；扇形①的圆心角的大小是______；（2）求这40个样本数据平均数、众数、中位数；（3）若该校九年级共有160名学生，估计该校理化实验操作得满分的学生有多少人．   21．（10分）计算：当时，求代数式的值   22．（10分）暑假期间，两位家长计划带领若干名学生去旅游，他们联系了报价均为每人1000元的两家旅行社．经协商，甲旅行社的优惠条件是：两位家长全额收费，学生都按7折收费；乙旅行社的优惠条件是：学生、家长都按8折收费．假设这两位家长带领x名学生去旅行，甲、乙旅行社的收费分别为y甲，y乙，（1）写出y甲，y乙与x的函数关系式．（2）学生人数在什么情况下，选择哪个旅行社合算？   23．（12分）再读教材:宽与长的比是 (约为0.618)的矩形叫做黄金矩形，黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步，如图②.把这个正方形折成两个相等的矩形,再把纸片展平.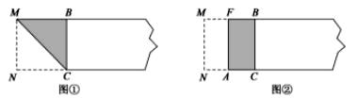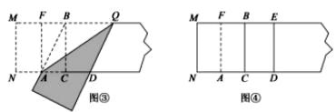第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处，第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形，问题解决:    （1）图③中AB=________(保留根号);    （2）如图③,判断四边形 BADQ的形状,并说明理由;    （3）请写出图④中所有的黄金矩形,并选择其中一个说明理由.    （4）结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、D2、D3、C4、B5、D6、D7、A8、B9、B10、B11、B12、B 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、、或．14、215、 (-2,-1)16、17、. 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）y1＝224x－4 800；y2＝240x－8 000；（2）当男生人数少于200时，购买B公司服装合算；当男生人数等于200时，购买A，B公司服装都一样；当男生人数大于200时，购买A公司服装合算，理由见解析19、（1）B（7，7）；（2）表格填写见解析；①,PQ长度的最小值是；②四边形OPBQ的面积不会发生变化；（3）t=3.5存在经过M，N两点的反比例函数.20、（1）10；；（2）8.3；9；8；（3）2821、（1）；（2）922、（1）y甲、y乙与x的函数关系式分别为：y甲=700x+2000，y乙=800x+1600；（2）当学生人数超过4人时，选择甲旅行社更省钱，当学生人数少于4人时，选择乙旅行社更省钱，学生人数等于4人时，选择甲、乙旅行社相等．23、（1）；(2)见解析;(3) 见解析; (4) 见解析.