2022-2023学年河南省漯河市召陵区数学七年级第二学期期末质量检测模拟试题含答案

2022-2023学年河南省漯河市召陵区数学七年级第二学期期末质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．若一个三角形各边的长度都扩大2倍，则扩大后的三角形各角的度数都（　　）

A．缩小2倍 B．不变 C．扩大2倍 D．扩大4倍

2．七位评委对参加普通话比赛的选手评分，比赛规则规定要去掉一个最高分和一个最低分，然后计 算剩下了 5 个分数的平均分作为选手的比赛分数，规则“去掉一个最高分和一个最低分”一定不会影 响这组数据的（   ）

A．平均数 B．中位数 C．极差 D．众数

3．如图，平行四边形ABCD的对角线AC与BD相交于点O，，垂足为E，，，．则AE的长为（　　　　）

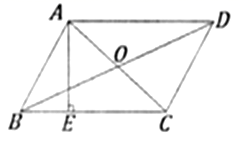
A． B．3 C． D．

4．如图，点A，B，C在一次函数的图象上，它们的横坐标依次为，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（　　）

A．1 B．3 C． D．

5．有一组数据：3，3，5，6，1．这组数据的众数为（　　）

A．3 B．5 C．6 D．1

6．下列式子中，属于最简二次根式的是：

A． B． C． D．

7．甲、乙、丙、丁四名射击队员考核赛的平均成绩（环）及方差统计如表，现要根据这些数据，从中选出一人参加比赛，如果你是教练员，你的选择是（　　）

A．甲 B．乙 C．丙 D．丁

8．若分式的值为0，则x的值为（　　）

A．-2 B．0 C．2 D．±2

9．如图，CD是△ABC的边AB上的中线，且CD＝AB，则下列结论错误的是（     ）

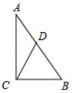
A．AD＝BD B．∠A＝30° C．∠ACB＝90° D．△ABC是直角三角形

10．如图，∠C＝90°，AB＝12，BC＝3，CD＝1．若∠ABD＝90°，则AD的长为(　　)

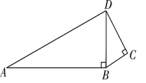
A．10 B．13 C．8 D．11

二、填空题(本大题共有6小题，每小题3分，共18分)

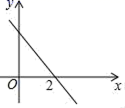
11．一次函数y＝kx+b(k≠0，k，b为常数)的图象如图所示，则关于x的不等式kx+b＜0的解集为______．

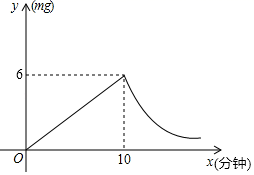
12．为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量与燃烧时间（分钟）成正比例；烧灼后，与成反比例（如图所示）.现测得药物分钟燃烧完，此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时，对人体方能无毒作用，那么从消毒开始，至少需要经过______分钟后，学生才能回到教室.

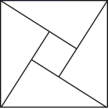
13．一个多边形每个外角都是，则这个多边形是_____边形．

14．如图是我国古代数学家赵爽的《勾股圆方图》，由四个全等的直角三角形和一个小正方形拼成的大正方形．如果图中大、小正方形的面积分别为52和4，直角三角形两条直角边分别为x，y，那么=_____．

15．若直线与坐标轴所围成的三角形的面积为6，则k的值为______．

16．一次函数图象过点日与直线平行，则一次函数解析式__________．

三、解下列各题(本大题共8小题，共72分)

17．（8分）在平面直角坐标系内，已知．

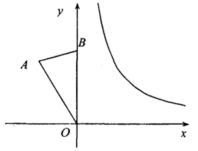
（1）点A的坐标为（____，______）；

（2）将绕点顺时针旋转度．

①当时，点恰好落在反比例函数的图象上，求的值；

②在旋转过程中，点能否同时落在上述反比例函数的图象上，若能，求出的值；若不能，请说明理由．

18．（8分）完成下面推理过程

如图，已知DE∥BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：

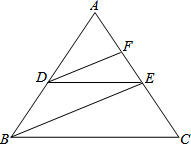
∵DE∥BC（已知）

∴∠ADE=　　　　　　．（　　　　　                    　  ）

∵DF、BE分别平分∠ADE、∠ABC，

∴∠ADF=　　　　　　，

∠ABE=　　　　　　．（　　　　　                       　）

∴∠ADF=∠ABE

∴DF∥　      　　．（　　　　　                         　）

∴∠FDE=∠DEB．  （　　　　　　                          ）

19．（8分）如图，已知直线与直线相交于点.

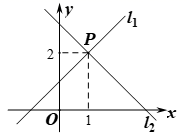
（1）求、的值；

（2）请结合图象直接写出不等式的解集.

20．（8分）如图，直线L：与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4）,线段OA上的动点M（与O，A不重合）从A点以每秒1个单位的速度沿x轴向左移动。

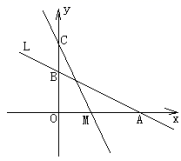
（1）求A、B两点的坐标；

（2）求△COM的面积S与M的移动时间t之间的函数关系式，并写出t的取值范围；

（3）当t何值时△COM≌△AOB，并求此时M点的坐标。

21．（8分）（1）计算

（2）解方程

22．（10分）某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如下表：

（1）若商场预计进货款为3500元，则这两种台灯各进多少盏．

（2）若设商场购进A型台灯m盏，销售完这批台灯所获利润为P，写出P与m之间的函数关系式．

（3）若商场规定B型灯的进货数量不超过A型灯数量的4倍，那么A型和B型台灯各进多少盏售完之后获得利润最多？此时利润是多少元．

23．（10分）计算：

（1）

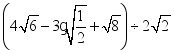
（2），，求的值.

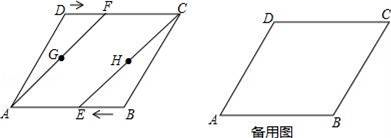
24．（12分）如图，在菱形ABCD中，AB=4cm，∠BAD=60°．动点E、F分别从点B、D同时出发，以1cm/s的速度向点A、C运动，连接AF、CE，取AF、CE的中点G、H，连接GE、FH．设运动的时间为ts（0＜t＜4）．

（1）求证：AF∥CE；

（2）当t为何值时，四边形EHFG为菱形；

（3）试探究：是否存在某个时刻t，使四边形EHFG为矩形，若存在，求出t的值，若不存在，请说明理由．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、D

4、B

5、A

6、A

7、C

8、C

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、x＞1

12、1

13、十二

14、1

15、±

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）A（-1，）；（2）①；②，理由见解析

18、∠ABC；两直线平行，同位角相等；∠ADE；∠ABC；角平分线定义；DF∥BE；同位角相等,两直线平行；两直线平行，内错角相等

19、（1），；（2）.

20、（1）A（4，0）、B（0，2）

（2）当0<t<4时， S△OCM=8-2t；

（3）当t=2秒时△COM≌△AOB，此时M（2，0）

21、（1）原式=；（2）x1=-1，x2=2.5；

22、（1）应购进A型台灯75盏，B型台灯25盏；（2）P=﹣5m+2000；（3）商场购进A型台灯20盏，B型台灯80盏，销售完这批台灯时获利最多，此时利润为1900元．

23、 (1) ;（2）.

24、（1）证明见解析；（2）t=1，（3）不存在某个时刻t，使四边形EHFG为矩形．