


2022-2023学年河南省漯河市数学七年级第二学期期末达标测试试题含答案
展开2022-2023学年河南省漯河市数学七年级第二学期期末达标测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.矩形ABCD的对角线AC、BD交于点O,下列结论不成立的是( )
A.AC=BD B.OA=OB C.OC=CD D.∠BCD=90°
2.某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按40%和60%来计算综合成绩.王老师本次招聘考试的笔试成绩为90分,面试成绩为85分,经计算他的综合成绩是( )
A.85分 B.87分 C.87.5分 D.90分
3.如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组![]() 的解是( )
的解是( )
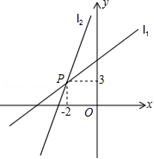
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列方程没有实数根的是( )
A.x3+2=0 B.x2+2x+2=0
C.![]() =x﹣1 D.
=x﹣1 D.![]() =0
=0
5.如果分式![]() 有意义,那么
有意义,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 或
或![]()
6.如果a为任意实数, 下列各式中一定有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC
8.用尺现作图的方法在一个平行四边形内作菱形![]() ,下列作法错误的是 ( )
,下列作法错误的是 ( )
A. B.
B.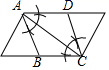 C.
C. D.
D.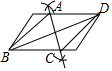
9.下列二次根式能与![]() 合并为一项的是( )
合并为一项的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲出发,沿直线匀速行驶经过乙港驶向丙港,最终达到丙港,设行驶x (h)后,船与乙港的距离为y (km),y与x的关系如图所示,则下列说法正确的是( )

A.甲港与丙港的距离是90km B.船在中途休息了0.5小时
C.船的行驶速度是45km/h D.从乙港到达丙港共花了1.5小时
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,在一张长为7cm,宽为5cm的矩形纸片上,现在剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的的高为_____________.

12.一次函数y=k(x-1)的图象经过点M(-1,-2),则其图象与y轴的交点是__________.
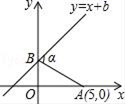
13.如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为_____.
14.已知点M(m,3)在直线![]() 上,则m=______.
上,则m=______.
15.一组数据从小到大排列:0、3、![]() 、5,中位数是4,则
、5,中位数是4,则![]() ________.
________.
16.如果多项式![]() 是一个完全平方式,那么k的值为______.
是一个完全平方式,那么k的值为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某校为美化校园,计划对面积为2000m2的区域进行绿化,安排甲、乙两个工程队完成,已知甲队每天完成绿化的面积是乙队每天完成绿化的面积的2倍,并且在独立完成面积为600m2区域的绿化时,甲队比乙队少用6天.
(1)甲、乙两个工程队每天能完成绿化的面积分别是多少?
(2)若学校每天需付给甲队的绿化费用为0.5万元,乙队为0.3万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
18.(8分)某经销商从市场得知如下信息:
| 某品牌空调扇 | 某品牌电风扇 |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?
19.(8分)解一元二次方程
(1)2x![]() +x-3=0 (2)
+x-3=0 (2)![]()
20.(8分)某市开展“环境治理留住青山绿水,绿色发展赢得金山银山”活动,对其周边的环境污染进行综合治理.![]() 年对
年对![]() 、
、![]() 两区的空气量进行监测,将当月每天的空气污染指数(简称:
两区的空气量进行监测,将当月每天的空气污染指数(简称:![]() )的平均值作为每个月的空气污染指数,并将
)的平均值作为每个月的空气污染指数,并将![]() 年空气污染指数绘制如下表.据了解,空气污染指数
年空气污染指数绘制如下表.据了解,空气污染指数![]() 时,空气质量为优:
时,空气质量为优:![]() 空气污染指数
空气污染指数![]() 时,空气质量为良:
时,空气质量为良:![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出![]() 、
、![]() 两区的空气污染指数的平均数;
两区的空气污染指数的平均数;
(2)请从平均数、众数、中位数、方差等统计量中选两个对![]() 区、
区、![]() 区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
21.(8分)某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
22.(10分)如图,在![]() 中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
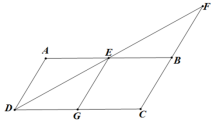
⑴求证:四边形AEGD为菱形;
⑵若![]() ,AD=2,求DF的长.
,AD=2,求DF的长.
23.(10分)如图,直线y=3x与反比例函数y=![]() (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.

(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=![]() (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.
①当t=![]() 时,求线段EF的长;
时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.
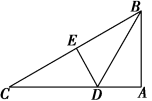
24.(12分)如图,已知BD是△ABC的角平分线,ED是BC的垂直平分线,∠BAC=90°,AD=1.
①求∠C的度数,②求CE的长.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、A
4、B
5、C
6、C
7、C
8、A
9、A
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、4或![]() 或
或![]()
12、 (0,-1)
13、![]()
14、2
15、5
16、8或-4
三、解下列各题(本大题共8小题,共72分)
17、(1)甲工程队每天能完成绿化的面积为3m1,乙工程队每天能完成绿化的面积为2m1.(1)至少应安排甲队工作10天.
18、(1)y=140x+6000(0<x≤50);(2)购进该品牌空调扇和电风扇各50台时,经销商可获利最大,最大利润是13000元.
19、(1)![]() (2)
(2)![]()
20、(1)A区的的空气污染指数的平均数是79,B区的的空气污染指数的平均数是80;(2)A区
21、(1)平均数:260件;中位数:240件;众数:240件(2)不合理,定额为240较为合理
22、(1)证明见解析;(2)4![]() .
.
23、(2)m=2;k=2;B(-2,-2);(2)①EF=8,②-2<t≤-![]() 或
或 ![]() ≤t<2
≤t<2
24、①∠C=10度;②CE=![]() .
.
河南省漯河市2023-2024学年数学九上期末达标检测试题含答案: 这是一份河南省漯河市2023-2024学年数学九上期末达标检测试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
2023-2024学年河南省漯河市郾城区数学八年级第一学期期末达标检测试题含答案: 这是一份2023-2024学年河南省漯河市郾城区数学八年级第一学期期末达标检测试题含答案,共7页。试卷主要包含了如图,下面推理中,正确的是等内容,欢迎下载使用。
2023-2024学年河南省漯河市名校数学八上期末达标检测模拟试题含答案: 这是一份2023-2024学年河南省漯河市名校数学八上期末达标检测模拟试题含答案,共7页。试卷主要包含了已知A,化简的结果为,不等式组的解集在数轴上可表示为,如图反映的过程是等内容,欢迎下载使用。












