


2022-2023学年浙江省宁波市东恩中学数学七年级第二学期期末监测模拟试题含答案
展开2022-2023学年浙江省宁波市东恩中学数学七年级第二学期期末监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.二次根式![]() 在实数范围内有意义,那么
在实数范围内有意义,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列由左到右的变形,属于因式分解的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.反比例函数![]() 的图象如图所示,以下结论错误的是( )
的图象如图所示,以下结论错误的是( )
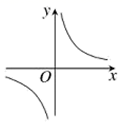
A.![]()
B.若点![]() 在图象上,则
在图象上,则![]()
C.在每个象限内,![]() 的值随
的值随![]() 值的增大而减小
值的增大而减小
D.若点![]() ,
,![]() 在图象上,则
在图象上,则![]()
4.在平面直角坐标系中,点![]() 与点
与点![]() 关于原点对称,则
关于原点对称,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.1 D.3
C.1 D.3
5.符![]() .则下列不等式变形错误的是( )
.则下列不等式变形错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD为矩形的是( )

A.∠ABC=90° B.AC=BD
C.AD=BC,AB∥CD D.∠BAD=∠ADC
7.如图,将三个同样的正方形的一个顶点重合放置,如果![]() °,
°,![]() °时,那么
°时,那么![]() 的度数是( )
的度数是( )
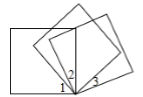
A.15° B.25° C.30° D.45°
8.如图,在菱形ABCD中,一动点P从点B出发,沿着B→C→D→A的方向匀速运动,最后到达点A,则点P在匀速运动过程中,△APB的面积y随时间x变化的图象大致是( )
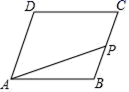
A. B.
B.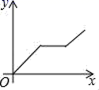
C.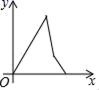 D.
D.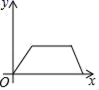
9.如图,在正方形![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
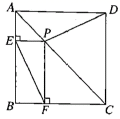
A.1.5 B.2 C.2.5 D.3
10.二次根式![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,最简二次根式有( )个.
中,最简二次根式有( )个.
A.1 个 B.2 个 C.3 个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分)
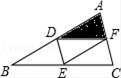
11.如图,在△ABC中,D,E,F,分别时AB,BC,AC,的中点,若平移△ADF平移,则图中能与它重合的三角形是 .(写出一个即可)
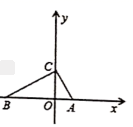
12.如图,在![]() 中,
中,![]() ,
,![]() ,斜边
,斜边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 的坐标为
的坐标为![]() .则直角边
.则直角边![]() 所在直线的解析式为__________.
所在直线的解析式为__________.
13.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级 | 参加人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是______.(填序号)
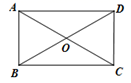
14.如图,□ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4,则□ABCD的面积等于________.
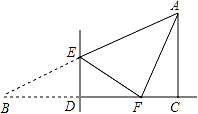
15.如图,在Rt△ABC中,∠ACB=90°,∠B=10°,BC=1.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为_____.
16.计算:![]() =_____.
=_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
| 国外品牌 | 国内品牌 |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
18.(8分)小王开车从甲地到乙地,去时走A线路,全程约100千米,返回时走B路线,全程约60千米.小王开车去时的平均速度比返回时的平均速度快20千米/小时,所用时间却比返回时多15分钟.若小王返回时的平均车速不低于70千米/小时,求小王开车返回时的平均速度.
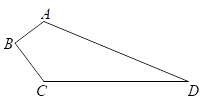
19.(8分)某小区有一块四边形空地ABCD,如图所示,现计划在这块地上种植每平方米60元的草坪用以美化环境,施工人员测得(单位:米):AB=3,BC=4,CD=12,DA=13,∠B=90°,求小区种植这种草坪需多少钱?
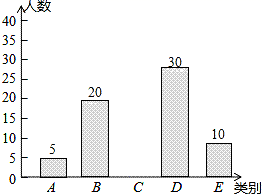
20.(8分)亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某校八年级学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)若把每天进行体育锻炼的时间在1小时以上定为锻炼达标,则被抽查学生的达标率是多少?
21.(8分)如图1,BD是正方形ABCD的对角线,BC=4,点H是AD边上的一动点,连接CH,作![]() ,使得HE=CH,连接AE。
,使得HE=CH,连接AE。
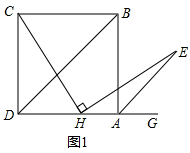
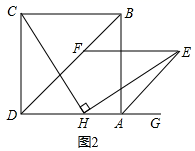
(1)求证:![]() ;
;
(2)如图2,过点E作EF//AD交对角线BD于点F,试探究:在点H的运动过程中,EF的长度是否为一个定值;如果是,请求出EF的长度。
22.(10分)在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.
(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;
(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;
(3)当点B,E,F在一条直线上时,求∠CBE的度数.(直接写出结果即可)
23.(10分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
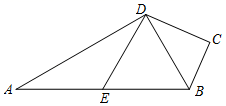
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=![]() ,求EC的长.
,求EC的长.
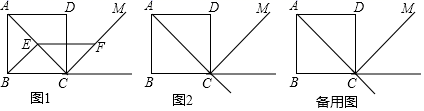
24.(12分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题:
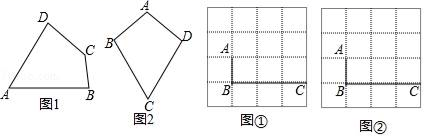
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °
(2)在探究等对角四边形性质时:
小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.
要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、C
5、B
6、C
7、A
8、D
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、△DBE(或△FEC).
12、y=![]() x+1
x+1
13、(1),(2).
14、16![]()
15、1或2
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)商场计划购进国外品牌手机20部,国内品牌手机30部;(2)当该商场购进国外品牌手机15部,国内品牌手机45部时,全部销售后获利最大,最大毛利润为3.15万元.
18、80千米/小时
19、小区种植这种草坪需要2160元.
20、 (1) 35;(2)答案见解析;(3)1<t≤1.5;(4)75%.
21、(1)见解析(2)EF为定值4
22、(1)EF=![]() BE;(2)EF=
BE;(2)EF=![]() BE,理由见解析;(3)当B,E,F在一条直线上时,∠CBE=22.5°
BE,理由见解析;(3)当B,E,F在一条直线上时,∠CBE=22.5°
23、(1)见解析;(2)![]() .
.
24、(1)140°,1°;(2)证明见解析;(3)见解析;(4)2![]() 或2
或2![]() .
.
浙江省宁波市东恩中学2023-2024学年数学八年级第一学期期末质量跟踪监视模拟试题含答案: 这是一份浙江省宁波市东恩中学2023-2024学年数学八年级第一学期期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列各式中,计算正确的是等内容,欢迎下载使用。
浙江省宁波市东恩中学2023-2024学年八上数学期末调研试题含答案: 这是一份浙江省宁波市东恩中学2023-2024学年八上数学期末调研试题含答案,共7页。试卷主要包含了在等腰三角形△ABC,-的相反数是,如果分式的值为0,则x的值是等内容,欢迎下载使用。
浙江省宁波市名校2022-2023学年七年级数学第二学期期末监测模拟试题含答案: 这是一份浙江省宁波市名校2022-2023学年七年级数学第二学期期末监测模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,点A,下列四个选项中运算错误的是等内容,欢迎下载使用。












