


2022-2023学年浙江省余姚市数学七下期末质量检测试题含答案
展开这是一份2022-2023学年浙江省余姚市数学七下期末质量检测试题含答案,共7页。试卷主要包含了高跟鞋的奥秘,八年级,分式等内容,欢迎下载使用。
2022-2023学年浙江省余姚市数学七下期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
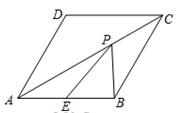
1.如图,在菱形![]() 中,
中,![]() =120°,点E是边
=120°,点E是边![]() 的中点,P是对角线
的中点,P是对角线![]() 上的一个动点,若AB=2,则PB+PE的最小值是( )
上的一个动点,若AB=2,则PB+PE的最小值是( )
A.1 B.![]() C.2 D.
C.2 D.![]()
2.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对边平行 C.对角互补 D.内角和为360°
3.在平面直角坐标系中,点![]() 位于
位于![]()
![]()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.高跟鞋的奥秘:当人肚脐以下部分的长![]() 与身高,的比值越接近0.618时,越给人以一种匀称的美感,如图,某女士身高
与身高,的比值越接近0.618时,越给人以一种匀称的美感,如图,某女士身高![]() ,脱去鞋后量得下半身长为
,脱去鞋后量得下半身长为![]() ,则建议她穿的高跟鞋高度大约为( )
,则建议她穿的高跟鞋高度大约为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.一个多边形每个外角都是![]() ,则该多边形的边数是( )
,则该多边形的边数是( )
A.4 B.5 C.6 D.7
6.如果一个直角三角形的两边分别是6,8,那么斜边上的中线是( )
A.4 B.5 C.4或5 D.3或5
7.下列所叙述的图形中,全等的两个三角形是( )
A.含有45°角的两个直角三角形 B.腰相等的两个等腰三角形
C.边长相等的两个等边三角形 D.一个钝角对应相等的两个等腰三角形
8.八年级(6)班一同学感冒发烧住院洽疗,护士为了较直观地了解这位同学这一天24h的体温和时间的关系,可选择的比较好的方法是( )
A.列表法 B.图象法
C.解析式法 D.以上三种方法均可
9.分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,最简分式的个数有( )
中,最简分式的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在正方形OABC中,点A的坐标是(﹣3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
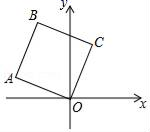
A.(﹣2,4),(1,3) B.(﹣2,4),(2,3)
C.(﹣3,4),(1,4) D.(﹣3,4),(1,3)
11.如图,小颖为测量学校旗杆AB的高度,她在E处放置一块镜子,然后退到C处站立,刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.5m,她离镜子的水平距离CE=0.5m,镜子E离旗杆的底部A处的距离AE=2m,且A、C、E三点在同一水平直线上,则旗杆AB的高度为( )
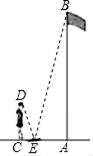
A.4.5m B.4.8m C.5.5m D.6 m
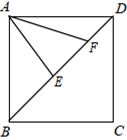
12.如图,正方形ABCD的边长为3,E、F是对角线BD上的两个动点,且EF=![]() ,连接AE、AF,则 AE+AF 的最小值为( )
,连接AE、AF,则 AE+AF 的最小值为( )
A.![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.甲、乙两人进行射击比赛,在相同条件下各射击 12 次,他们的平均成绩各为 8 环,12 次射击成绩的方差分别是:S 甲=3,S 乙=2.5,成绩较为稳定的是__________.(填 “甲”或“乙”)
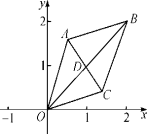
14.如图,已知菱形OABC的顶点O(0,0),B(2,2),则菱形的对角线交点D的坐标为____;若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,点D的坐标为_____.
15.将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是 .
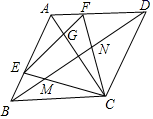
16.如图,已知边长为4的菱形ABCD中,AC=BC,E,F分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD与点M,N,给出下列结论:①∠AFC=∠AGE;②EF=BE+DF;③△ECF面积的最小值为3![]() ,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
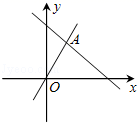
17.如图,函数y=2x和y=ax+5的图象相交于A(m,3),则不等式2x<ax+5的解集为 .
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
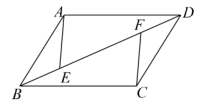
18.(5分)如图,![]() 中,
中,![]() ,
,![]() 两点在对角线
两点在对角线![]() 上,
上,![]() .
.
(1)求证:![]() ;
;
(2)当四边形![]() 为矩形时,连结
为矩形时,连结![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
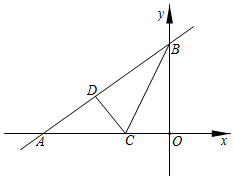
19.(5分)已知:直线y=![]() 与x轴、y轴分别相交于点A和点B,点C在线段AO上.将△CBO沿BC折叠后,点O恰好落在AB边上点D处.
与x轴、y轴分别相交于点A和点B,点C在线段AO上.将△CBO沿BC折叠后,点O恰好落在AB边上点D处.
(1)直接写出点A、点B的坐标:
(2)求AC的长;
(3)点P为平面内一动点,且满足以A、B、C、P为顶点的四边形为平行四边形,请直接回答:
①符合要求的P点有几个?
②写出一个符合要求的P点坐标.
20.(8分)(1)解不等式组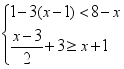
(2)先化简分式![]() ,然后在0,1,2,3中选一个你认为合适的a值,代入求值。
,然后在0,1,2,3中选一个你认为合适的a值,代入求值。
21.(10分)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
22.(10分)如图,直线y=2x+6交x轴于A,交y轴于B.
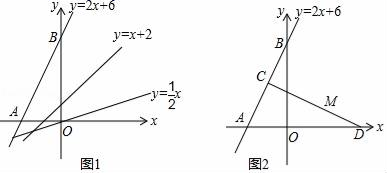
(1)直接写出A( , ),B( , );
(2)如图1,点E为直线y=x+2上一点,点F为直线y=![]() x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
(3)如图2,点C(m,n)为线段AB上一动点,D(﹣7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.
23.(12分)如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
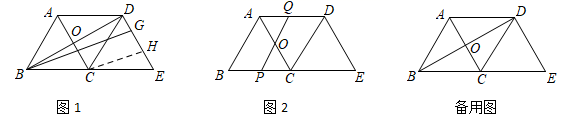
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;
(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.
(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、C
4、C
5、B
6、C
7、C
8、B
9、B
10、A
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、乙
14、 (1,1) (-1,-1).
15、(0,1).
16、①③④
17、x<![]() .
.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)证明见解析;(1)1.
19、(1)B(0,6),A(﹣8,0).(2)1;(3)①3个;②P1(﹣1,6),P2(﹣11,﹣6),P3(1,6).
20、(1)﹣2<x≤1(2)见解析
21、 (1) 众数为15;(2) 3,4,15;8;(3) 月销售额定为18万,有一半左右的营业员能达到销售目标.
22、(1)﹣3,0,0,6;(2)E(5,7),F(2,1)或E(11,13),F(﹣14,﹣7);(3)![]() .
.
23、(1)1;(1)y=1x+10(![]() ≤x≤4),当x=
≤x≤4),当x=![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ;(3)能,满足条件的PQ的值为:
;(3)能,满足条件的PQ的值为:![]() 或2或3.
或2或3.
相关试卷
这是一份浙江省金华市2022-2023学年数学七下期末教学质量检测模拟试题含答案,共6页。试卷主要包含了下列说法等内容,欢迎下载使用。
这是一份浙江省杭州市高桥2022-2023学年七下数学期末质量检测试题含答案,共7页。
这是一份浙江省宁波市余姚市2022-2023学年数学七下期末复习检测试题含答案,共7页。试卷主要包含了若分式口,的运算结果为x,下列式子成立的是,下列几何图形是中心对称图形的是等内容,欢迎下载使用。












