

2022-2023学年浙江省温州市五校七年级数学第二学期期末质量跟踪监视试题含答案
展开
这是一份2022-2023学年浙江省温州市五校七年级数学第二学期期末质量跟踪监视试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列方程中是二项方程的是,在平面直角坐标系中,点在等内容,欢迎下载使用。
2022-2023学年浙江省温州市五校七年级数学第二学期期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.已知一次函数y=ax+b(a、b为常数且a≠0)的图象经过点(1,3)和(0,-2),则a-b的值为( )A.-1 B.-3 C.3 D.72.计算![]() 的结果等于( )A.
的结果等于( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,在平行四边形ABCD中,下列各式不一定正确的是( )
3.如图,在平行四边形ABCD中,下列各式不一定正确的是( )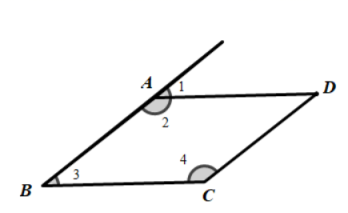 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
4.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )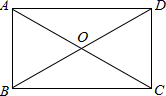 A.12 B.14 C.16 D.185.如果ab>0,a+b<0,那么下面各式:①
A.12 B.14 C.16 D.185.如果ab>0,a+b<0,那么下面各式:①![]() ; ②
; ②![]() =1;③
=1;③![]() =-b.其中正确的是( )A.①② B.①③ C.①②③ D.②③6.如图,在
=-b.其中正确的是( )A.①② B.①③ C.①②③ D.②③6.如图,在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于
于![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长度为( )
的长度为( )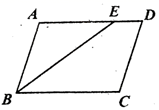 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.下列方程中是二项方程的是( )A.
7.下列方程中是二项方程的是( )A.![]() ; B.
; B.![]() =0; C.
=0; C.![]() ; D.
; D.![]() =1.8.在平面直角坐标系中,点
=1.8.在平面直角坐标系中,点![]() 在( )A.
在( )A.![]() 轴正半轴上 B.
轴正半轴上 B.![]() 轴负半轴上 C.
轴负半轴上 C.![]() 轴正半轴上 D.
轴正半轴上 D.![]() 轴负半轴上9.已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )A.5 B.7 C.15 D.1710.下列长度的三条线段能组成三角形的是( )A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8二、填空题(本大题共有6小题,每小题3分,共18分)11.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则关于x的一元一次不等式kx<﹣x+3的解集是_____.
轴负半轴上9.已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )A.5 B.7 C.15 D.1710.下列长度的三条线段能组成三角形的是( )A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8二、填空题(本大题共有6小题,每小题3分,共18分)11.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则关于x的一元一次不等式kx<﹣x+3的解集是_____.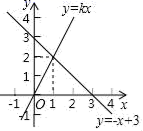 12.如图,将一块边长为 12 cm 正方形纸片 ABCD 的顶点 A 折叠至DC 边上的 E 点,使 DE=5,折痕为 PQ,则 PQ 的长为_________cm.
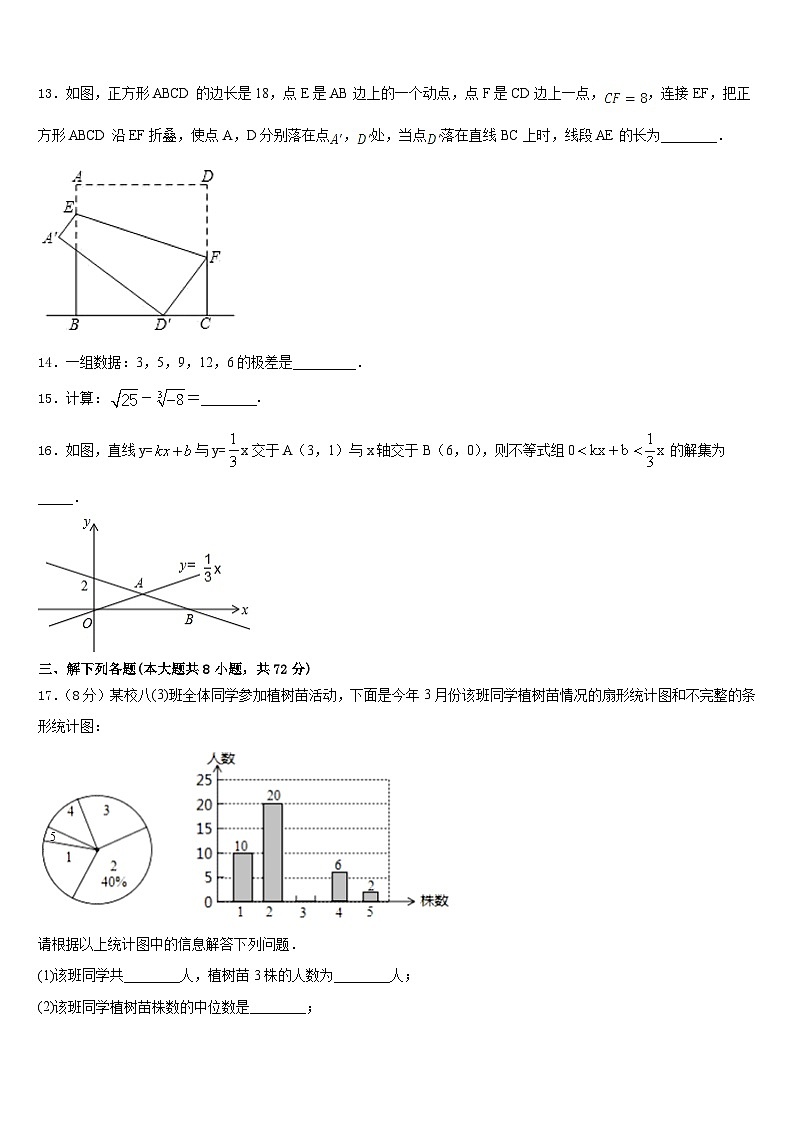
12.如图,将一块边长为 12 cm 正方形纸片 ABCD 的顶点 A 折叠至DC 边上的 E 点,使 DE=5,折痕为 PQ,则 PQ 的长为_________cm.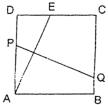 13.如图,正方形ABCD的边长是18,点E是AB边上的一个动点,点F是CD边上一点,
13.如图,正方形ABCD的边长是18,点E是AB边上的一个动点,点F是CD边上一点,![]() ,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点
,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在直线BC上时,线段AE的长为________.
落在直线BC上时,线段AE的长为________.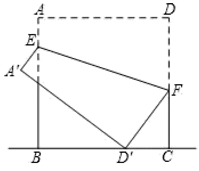 14.一组数据:3,5,9,12,6的极差是_________.15.计算:
14.一组数据:3,5,9,12,6的极差是_________.15.计算:![]() -
-![]() =________.16.如图,直线y=
=________.16.如图,直线y=![]() 与y=
与y=![]() x交于A(3,1)与x轴交于B(6,0),则不等式组0
x交于A(3,1)与x轴交于B(6,0),则不等式组0![]() 的解集为_____.
的解集为_____.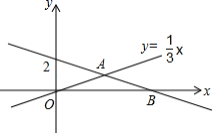 三、解下列各题(本大题共8小题,共72分)17.(8分)某校八(3)班全体同学参加植树苗活动,下面是今年3月份该班同学植树苗情况的扇形统计图和不完整的条形统计图:
三、解下列各题(本大题共8小题,共72分)17.(8分)某校八(3)班全体同学参加植树苗活动,下面是今年3月份该班同学植树苗情况的扇形统计图和不完整的条形统计图: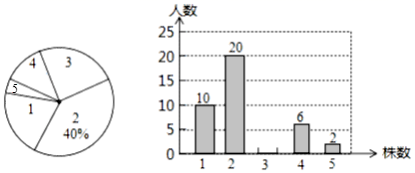 请根据以上统计图中的信息解答下列问题.(1)该班同学共________人,植树苗3株的人数为________人;(2)该班同学植树苗株数的中位数是________;(3)小明用以下方法计算该班同学平均植树苗的株数是:
请根据以上统计图中的信息解答下列问题.(1)该班同学共________人,植树苗3株的人数为________人;(2)该班同学植树苗株数的中位数是________;(3)小明用以下方法计算该班同学平均植树苗的株数是:![]() (株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果. 18.(8分)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果. 18.(8分)如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.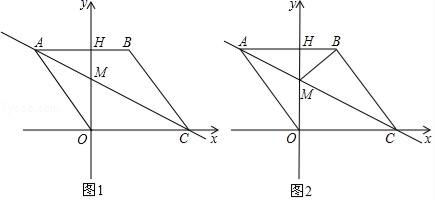 (1)菱形ABCO的边长 (2)求直线AC的解析式;(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,①当0<t<
(1)菱形ABCO的边长 (2)求直线AC的解析式;(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,①当0<t<![]() 时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值. 19.(8分)如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.求证:∠P=90°﹣
时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值. 19.(8分)如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.求证:∠P=90°﹣![]() ∠C;
∠C;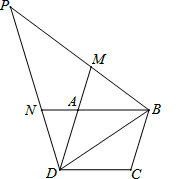 20.(8分) (1)求不等式
20.(8分) (1)求不等式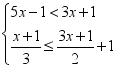 组的整数解.(2)解方程组:
组的整数解.(2)解方程组: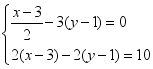 21.(8分)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
21.(8分)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.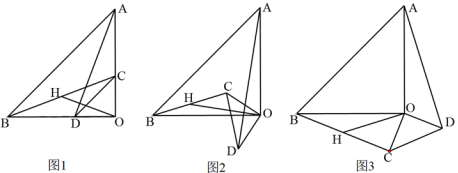 (1)如图1所示,求证:
(1)如图1所示,求证:![]() 且
且![]() (2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论 22.(10分)如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论 22.(10分)如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.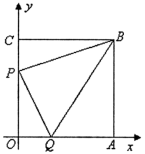 (1)写出 B 点的坐标;(2)填写下表:时间 t(单位:秒)123456OP 的长度 OQ 的长度 PQ 的长度 四边形 OPBQ 的面积 ①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由. 23.(10分)为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元,售价320元;乙种服装每件进价150元,售价280元.(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货? 24.(12分)如图,□ABCD的对角线AC、BD相交于点O,AC平分∠BAD,DP//AC,CP//BD.
(1)写出 B 点的坐标;(2)填写下表:时间 t(单位:秒)123456OP 的长度 OQ 的长度 PQ 的长度 四边形 OPBQ 的面积 ①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由. 23.(10分)为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元,售价320元;乙种服装每件进价150元,售价280元.(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货? 24.(12分)如图,□ABCD的对角线AC、BD相交于点O,AC平分∠BAD,DP//AC,CP//BD.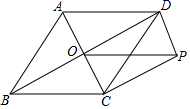 (1)求证:四边形ABCD是菱形;(2)若AC=4,BD=6,求OP的长. 参考答案 一、选择题(每小题3分,共30分)1、D2、D3、D4、A5、D6、B7、C8、D9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、x<112、1313、4或114、115、116、3<x<1 三、解下列各题(本大题共8小题,共72分)17、 (1)50,12;(2)2;(3)小明的计算不正确,正确的计算为2.4株18、(1)5;(2)直线AC的解析式y=﹣
(1)求证:四边形ABCD是菱形;(2)若AC=4,BD=6,求OP的长. 参考答案 一、选择题(每小题3分,共30分)1、D2、D3、D4、A5、D6、B7、C8、D9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、x<112、1313、4或114、115、116、3<x<1 三、解下列各题(本大题共8小题,共72分)17、 (1)50,12;(2)2;(3)小明的计算不正确,正确的计算为2.4株18、(1)5;(2)直线AC的解析式y=﹣![]() x+
x+![]() ;(3)见解析.19、证明见解析.20、(1)解集为
;(3)见解析.19、证明见解析.20、(1)解集为![]() ,整数解是-1,0;(2)
,整数解是-1,0;(2)![]() 21、(1)详见解析;(2)详见解析.22、(1)B(7,7);(2)表格填写见解析;①,PQ长度的最小值是
21、(1)详见解析;(2)详见解析.22、(1)B(7,7);(2)表格填写见解析;①,PQ长度的最小值是![]() ;②四边形OPBQ的面积不会发生变化;(3)t=3.5存在经过M,N两点的反比例函数.23、(1)购进甲、乙两种服装2件、1件(2)共有11种方案(3)购进甲种服装70件,乙种服装130件24、(1)见解析;(2)
;②四边形OPBQ的面积不会发生变化;(3)t=3.5存在经过M,N两点的反比例函数.23、(1)购进甲、乙两种服装2件、1件(2)共有11种方案(3)购进甲种服装70件,乙种服装130件24、(1)见解析;(2)![]()
相关试卷
这是一份浙江省温州市瑞安市四校联考2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,若点P等内容,欢迎下载使用。
这是一份浙江省宁波江北区四校联考2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了已知,,则的结果为等内容,欢迎下载使用。
这是一份广东省惠州惠城区五校联考2022-2023学年数学七年级第二学期期末质量跟踪监视试题含答案,共6页。试卷主要包含了下列式子从左到右变形错误的是等内容,欢迎下载使用。









