


2022-2023学年浙江省温州市苍南县数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开
这是一份2022-2023学年浙江省温州市苍南县数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了若分式有意义,则x,y满足,下列说法不正确的是,一元二次方程 x2= x的根是等内容,欢迎下载使用。
2022-2023学年浙江省温州市苍南县数学七年级第二学期期末质量跟踪监视模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.实数![]() 、
、![]() 在数轴上对应的位置如图,化简
在数轴上对应的位置如图,化简![]() 等于( )
等于( )![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.某学习小组7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16,则这组数据中位数是( )A.12 B.13 C.14 D.173.在四边形
2.某学习小组7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16,则这组数据中位数是( )A.12 B.13 C.14 D.173.在四边形![]() 中,
中,![]() ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A.
,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.若分式
4.若分式![]() 有意义,则x,y满足( )A.2x≠y B.x≠0且y≠0 C.2x=y D.2x+y=05.如图,若平行四边形ABCD的周长为40cm,BC=
有意义,则x,y满足( )A.2x≠y B.x≠0且y≠0 C.2x=y D.2x+y=05.如图,若平行四边形ABCD的周长为40cm,BC=![]() AB,则BC=( )
AB,则BC=( )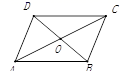 A.16crn B.14cm C.12cm D.8cm6.下列说法不正确的是( )A.有两组对边分别平行的四边形是平行四边形B.平行四边形的对角线互相平分C.平行四边形的对边平行且相等D.平行四边形的对角互补,邻角相等7.如图,在▱ABCD中,已知
A.16crn B.14cm C.12cm D.8cm6.下列说法不正确的是( )A.有两组对边分别平行的四边形是平行四边形B.平行四边形的对角线互相平分C.平行四边形的对边平行且相等D.平行四边形的对角互补,邻角相等7.如图,在▱ABCD中,已知![]() ,
,![]() ,AE平分
,AE平分![]() 交BC于点E,则CE长是
交BC于点E,则CE长是![]()
![]()
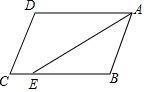 A.8cm B.5cm C.9cm D.4cm8.用长为28米的铝材制成一个矩形窗框,使它的面积为25平方米.若设它的一边长为x米,根据题意列出关于x的方程为( )A.x(28﹣x)=25 B.2x(14﹣x)=25C.x(14﹣x)=25 D.
A.8cm B.5cm C.9cm D.4cm8.用长为28米的铝材制成一个矩形窗框,使它的面积为25平方米.若设它的一边长为x米,根据题意列出关于x的方程为( )A.x(28﹣x)=25 B.2x(14﹣x)=25C.x(14﹣x)=25 D.![]() 9.一元二次方程 x2= x的根是( )A.
9.一元二次方程 x2= x的根是( )A.![]() =0,
=0,![]() =1 B.
=1 B.![]() =0,
=0,![]() =-1 C.
=-1 C.![]() =
=![]() =0 D.
=0 D.![]() =
=![]() =110.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A.7,24,25 B.
=110.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A.7,24,25 B.![]() ,
,![]() ,
,![]() C.6,8,10 D.9,12,15二、填空题(本大题共有6小题,每小题3分,共18分)11.如图所示,△ABC为等边三角形,D为AB的中点,高AH=10 cm,P为AH上一动点,则PD+PB的最小值为_______cm.
C.6,8,10 D.9,12,15二、填空题(本大题共有6小题,每小题3分,共18分)11.如图所示,△ABC为等边三角形,D为AB的中点,高AH=10 cm,P为AH上一动点,则PD+PB的最小值为_______cm.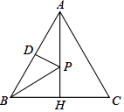 12.如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,···的顶点B1,B2,B3,···在x轴上,顶点C1,C2,C3···在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3, 则点C5的纵坐标是_____.
12.如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,···的顶点B1,B2,B3,···在x轴上,顶点C1,C2,C3···在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3, 则点C5的纵坐标是_____.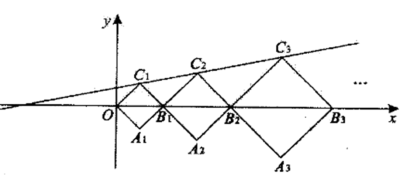 13.用一块长80cm,宽60cm的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为1500cm2的无盖长方体纸盒,则截去的小正方形的边长为___________.14.要使代数式
13.用一块长80cm,宽60cm的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为1500cm2的无盖长方体纸盒,则截去的小正方形的边长为___________.14.要使代数式![]() 有意义,则
有意义,则![]() 的取值范围是________.15.先化简:
的取值范围是________.15.先化简:![]() ,再对a选一个你喜欢的值代入,求代数式的值.16.如图,已知矩形ABCD的边AB=3,AD=8,顶点A、D分别在x轴、y轴上滑动,在矩形滑动过程中,点C到原点O距离的最大值是______.
,再对a选一个你喜欢的值代入,求代数式的值.16.如图,已知矩形ABCD的边AB=3,AD=8,顶点A、D分别在x轴、y轴上滑动,在矩形滑动过程中,点C到原点O距离的最大值是______.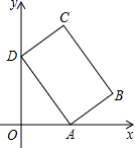 三、解下列各题(本大题共8小题,共72分)17.(8分)如图1,在平画直角坐标系中,直线
三、解下列各题(本大题共8小题,共72分)17.(8分)如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.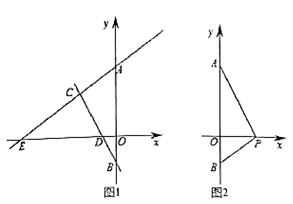 (1)直接写出直线
(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.(2)在直线
______.(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;(3)如图2,在
的坐标;(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标. 18.(8分)定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线
的坐标. 18.(8分)定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,若
上,若![]() ,则四边形
,则四边形![]() 是半对角四边形.(1)如图1,已知
是半对角四边形.(1)如图1,已知![]() ,
,![]() ,
,![]() ,若直线
,若直线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,则AB的长是____,CD的长是______;(2)如图2,点
,则AB的长是____,CD的长是______;(2)如图2,点![]() 是矩形
是矩形![]() 的边
的边![]() 上一点,
上一点,![]() ,
,![]() .若四边形
.若四边形![]() 为半对角四边形,求
为半对角四边形,求![]() 的长;(3)如图3,以
的长;(3)如图3,以![]() 的顶点
的顶点![]() 为坐标原点,边
为坐标原点,边![]() 所在直线为
所在直线为![]() 轴,对角线
轴,对角线![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.点
轴,建立平面直角坐标系.点![]() 是边
是边![]() 上一点,满足
上一点,满足![]() .①求证:四边形
.①求证:四边形![]() 是半对角四边形;②当
是半对角四边形;②当![]() ,
,![]() 时,将四边形
时,将四边形![]() 向右平移
向右平移![]() 个单位后,恰有两个顶点落在反比例函数
个单位后,恰有两个顶点落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值.
的值.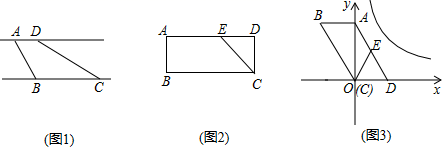 19.(8分)某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:(1)“基础电价”是____________元
19.(8分)某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:(1)“基础电价”是____________元 ![]() 度;(2)求出当x>240 时,y与x的函数表达式;(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?
度;(2)求出当x>240 时,y与x的函数表达式;(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?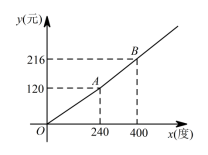 20.(8分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图1摆放时,都可以用“面积法”来证明,请你利用图1或图1证明勾股定理(其中∠DAB=90°)求证:a1+b1=c1.
20.(8分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图1摆放时,都可以用“面积法”来证明,请你利用图1或图1证明勾股定理(其中∠DAB=90°)求证:a1+b1=c1.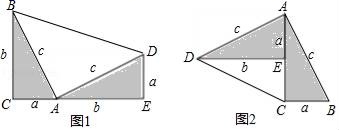 21.(8分)如图所示的是小聪课后自主学习的一道题,参照小聪的解题思路,回答下列问题:若
21.(8分)如图所示的是小聪课后自主学习的一道题,参照小聪的解题思路,回答下列问题:若![]() ,求m、n的值..小聪的解答:∵
,求m、n的值..小聪的解答:∵![]() ,∴
,∴![]() ,∴
,∴![]() ,而
,而![]() ,∴
,∴![]() ,∴
,∴![]() .(1)
.(1)![]() ,求a和b的值.(2)已知
,求a和b的值.(2)已知![]() 的三边长a、b、c满足
的三边长a、b、c满足![]() ,关于此三角形的形状有以下命题:①它是等边三角形;②它是等腰三角形;③它是直角三角形.其中是真命题的有_____.(填序号) 22.(10分)如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).(1)求CD的长;(2)当四边形PBQD为平行四边形时,求t的值;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理
,关于此三角形的形状有以下命题:①它是等边三角形;②它是等腰三角形;③它是直角三角形.其中是真命题的有_____.(填序号) 22.(10分)如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).(1)求CD的长;(2)当四边形PBQD为平行四边形时,求t的值;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理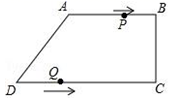
 23.(10分)如图,
23.(10分)如图,![]() 中,
中,![]() 、
、![]() 两点在对角线
两点在对角线![]() 上,且
上,且![]() .
.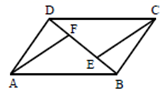 求证:
求证:![]() . 24.(12分)某景区的门票销售分两类:一类为散客门票,价格为
. 24.(12分)某景区的门票销售分两类:一类为散客门票,价格为![]() 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票![]() 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打![]() 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游![]() 人,购买门票需要
人,购买门票需要![]() 元(1)如果每人分别买票,求
元(1)如果每人分别买票,求![]() 与
与![]() 之间的函数关系式:(2)如果购买团体票,求
之间的函数关系式:(2)如果购买团体票,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式. 参考答案 一、选择题(每小题3分,共30分)1、B2、C3、A4、A5、D6、D7、B8、C9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1012、(
之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式. 参考答案 一、选择题(每小题3分,共30分)1、B2、C3、A4、A5、D6、D7、B8、C9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1012、(![]() ,
,![]() )13、1cm14、
)13、1cm14、![]() 且
且![]() 15、
15、![]() ;316、1 三、解下列各题(本大题共8小题,共72分)17、(1)
;316、1 三、解下列各题(本大题共8小题,共72分)17、(1)![]() ,22;(2)
,22;(2)![]() ;(3)
;(3)![]() 18、(1)2;
18、(1)2;![]() ;(2)AD=3;(3)①证明见解析;②
;(2)AD=3;(3)①证明见解析;②![]() 的值为为
的值为为![]() 或
或![]() .19、(1)0.5(2)y=0.6x-24(3)紫豪家这个月用电量为260度20、见解析.21、(1)
.19、(1)0.5(2)y=0.6x-24(3)紫豪家这个月用电量为260度20、见解析.21、(1)![]() ;(2)①②22、(1)1;(2)2;(3)不存在.理由见解析23、见解析24、(1)
;(2)①②22、(1)1;(2)2;(3)不存在.理由见解析23、见解析24、(1)![]() ;(2)y=32x(x⩾10);(3)8人以下买散客票; 8人以上买团体票;恰好8人时,即可按10人买团体票,可买散客票.
;(2)y=32x(x⩾10);(3)8人以下买散客票; 8人以上买团体票;恰好8人时,即可按10人买团体票,可买散客票.
相关试卷
这是一份浙江省温州市翔升2023-2024学年九年级数学第一学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了下列事件中,必然发生的为,如图,在中,,则等于等内容,欢迎下载使用。
这是一份浙江省杭州市朝晖中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了下列分式中,是最简分式的是等内容,欢迎下载使用。
这是一份2022-2023学年浙江省温州市秀山中学数学七年级第二学期期末质量跟踪监视试题含答案,共6页。试卷主要包含了答题时请按要求用笔,若点等内容,欢迎下载使用。









