2022-2023学年海南省省直辖县七下数学期末学业质量监测模拟试题含答案

2022-2023学年海南省省直辖县七下数学期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．下列各式正确的是（    ）

A．= ±3                      B．= ±3                      C．=3                      D．=-3

2．某公司10名职工的5月份工资统计如下，该公司10名职工5月份工资的众数和中位数分别是(    )

A．2400元、2400元

B．2400元、2300元

C．2200元、2200元

D．2200元、2300元

3．已知关于的方程的两根互为倒数，则的值为（  ）

A． B． C． D．

4．若代数式 在实数范围内有意义，则的取值范围是（  ）

A． B． C． D．且

5．定义：如果一个关于的分式方程的解等于，我们就说这个方程叫差解方程．比如：就是个差解方程．如果关于的分式方程是一个差解方程，那么的值是（  ）

A． B． C． D．

6．下列方程没有实数根的是（　　）

A．x3+2＝0 B．x2+2x+2＝0

C．＝x﹣1 D．＝0

7．下列说法中，正确的是（      ）

A．一组对边平行，另一组对边相等的四边形是平行四边形 B．对角线相等的四边形是矩形

C．有一组邻边相等的矩形是正方形 D．对角线互相垂直的四边形是菱形

8．一组数据5，2，3，5，4，5的众数是（　　）

A．3 B．4 C．5 D．8

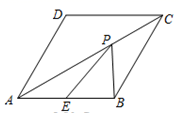
9．如图，在菱形中，=120°，点E是边的中点，P是对角线上的一个动点，若AB=2，则PB+PE的最小值是（    ）

A．1 B． C．2 D．

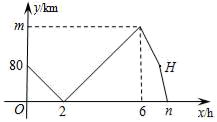
10．甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.1．其中说法正确的是（　　）

A．①②③ B．①②④ C．①③④ D．①②③④

二、填空题(本大题共有6小题，每小题3分，共18分)

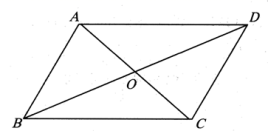
11．如图，在平行四边形中，度，，，则______.

12．将分别写有“绿色闵行”、“垃圾分类”、“要先行”的三张大小、质地相同的卡片随机排列，那么恰好排列成“绿色闵行垃圾分类要先行”的概率是__________．

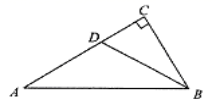
13．如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD=_______.

14．分解因式：=________．

15．    若A（x1，y1）和B（x2，y2）在反比例函数的图象上，且0＜x1＜x2，则y1与y2的大小关系是y1       y2；

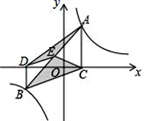
16．如图，点A，B在反比例函数（k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是______．

三、解下列各题(本大题共8小题，共72分)

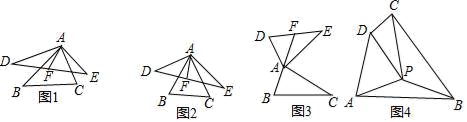
17．（8分）我们定义：如果两个三角形的两组对应边相等，且它们的夹角互补，我们就把其中一个三角形叫做另一个三角形的“夹补三角形”，同时把第三边的中线叫做“夹补中线．例如：图1中，△ABC与△ADE的对应边AB＝AD，AC＝AE，∠BAC+∠DAE＝180°，AF是DE边的中线，则△ADE就是△ABC的“夹补三角形”，AF叫做△ABC的“夹补中线”．

特例感知：

（1）如图2、图3中，△ABC与△ADE是一对“夹补三角形”，AF是△ABC的“夹补中线”；

①当△ABC是一个等边三角形时，AF与BC的数量关系是：　   　；

②如图3当△ABC是直角三角形时，∠BAC＝90°，BC＝a时，则AF的长是　   　；

猜想论证：

（2）在图1中，当△ABC为任意三角形时，猜想AF与BC的关系，并给予证明．

拓展应用：

（3）如图4，在四边形ABCD中，∠DCB＝90°，∠ADC＝150°，BC＝2AD＝6，CD＝，若△PAD是等边三角形，求证：△PCD是△PBA的“夹补三角形”，并求出它们的“夹补中线”的长．

18．（8分）某校举办的八年级学生数学素养大赛共设个项目:七巧板拼图，趣题巧解，数学应用，每个项目得分都按一定百分比折算后计入总分，总分高的获胜，下表为小米和小麦两位同学的得分情况（单位:分）:

若七巧板拼图，趣题巧解，数学应用三项得分分别按折算计入总分，最终谁能获胜?

若七巧板拼图按折算，小麦           （填“可能”或“不可能”）获胜．

19．（8分）某工厂车间为了了解工人日均生产能力的情况，随机抽取10名工人进行测试，将获得数据制成如下统计图.

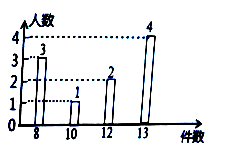
（1）求这10名工人的日均生产件数的平均数、众数、中位数；

（2）若日均生产件数不低于12件为优秀等级，该工厂车间共有工人120人，估计日均生产能力为“优秀”等级的工人约为多少人？

20．（8分）某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况，随机调查了部分学生最喜爱哪一类节目（被调查的学生只选一类并且没有不选择的），并将调查结果制成了如下的两个统计图（不完整）．请你根据图中所提供的信息，完成下列问题：

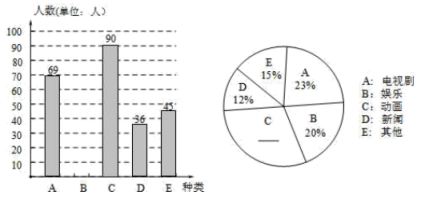
（1）本次调查的学生人数为__________，娱乐节目在扇形统计图中所占圆心角的度数是__________度．

（2）请将条形统计图补充完整：

（3）若该中学有2000名学生，请估计该校喜爱动画节目的人数．

21．（8分）已知x=+1 , y=－1 , 求x2+xy+y2的值．

22．（10分）如下4个图中，不同的矩形ABCD，若把D点沿AE对折，使D点与BC上的F点重合；

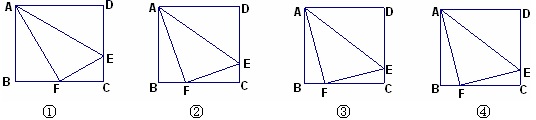
（1）图①中，若DE︰EC=2︰1，求证：△ABF∽△AFE∽△FCE；并计算BF︰FC；

（2）图②中若DE︰EC=3︰1，计算BF︰FC=     ；图③中若DE︰EC=4︰1，计算BF︰FC=     ；

（3）图④中若DE︰EC=︰1，猜想BF︰FC=       ；并证明你的结论

23．（10分）如图，在平面直角坐标系中，两点分别是轴和轴正半轴上两个动点，以三点为顶点的矩形的面积为24，反比例函数（为常数且）的图象与矩形的两边分别交于点.

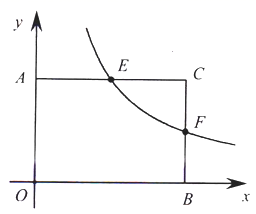
（1）若且点的横坐标为3.

①点的坐标为，点的坐标为（不需写过程，直接写出结果）；

②在轴上是否存在点，使的周长最小？若存在，请求出的周长最小值；若不存在，请说明理由.

（2）连接，在点的运动过程中，的面积会发生变化吗？若变化，请说明理由，若不变，请用含的代数式表示出的面积.

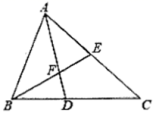
24．（12分）如图，在中，AD平分交BC于点D，F为AD上一点，且，BF的延长线交AC于点E．

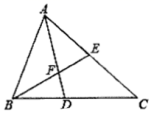
   备用图

（1）求证：；

（2）若，，，求DF的长；

参考答案

一、选择题(每小题3分,共30分)

1、C

2、A

3、C

4、D

5、D

6、B

7、C

8、C

9、B

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、

13、1

14、

15、>；

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）AF＝BC；a；（2）猜想：AF＝BC，（3）

18、（1）小麦获胜；（2）不可能

19、（1）平均数为11，众数为13，中位数为12.（2）优秀等级的工人约为72人.

20、 (1) 300，72°;(2)详见解析;(3)600.

21、7

22、（1）根据折叠的性质及矩形的性质可证得△ABF∽△AFE∽△FCE，再根据相似三角形的性质求解即可，1:1；（2）1:2，1:3；（3）1︰（n-1）

23、（1）①点坐标为，点坐标为；②存在，周长；

（2）不变，的面积为

24、（1）详见解析；（2）