

2022-2023学年海南省洋浦中学数学七下期末统考试题含答案
展开2022-2023学年海南省洋浦中学数学七下期末统考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.莒南县欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 | 面试 | 86 | 91 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
根据录用程序,作为人民教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲 B.乙 C.丙 D.丁
2.为了了解某市八年级女生的体能情况,从某校八年级的甲、乙两班各抽取27名女生进行一分钟跳绳次数的测试,测试数据统计如下:
| 人数 | 中位数 | 平均数 |
甲班 | 27 | 104 | 97 |
乙班 | 27 | 106 | 96 |
如果每分钟跳绳次数大于或等于105为优秀,则甲、乙两班优秀率的大小关系是( )
A.甲优<乙优 B.甲优>乙优 C.甲优=乙优 D.无法比较
3.用配方法解关于x的方程x2+px+q=0时,此方程可变形为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.不等式5+2x <1的解集在数轴上表示正确的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如果把分式![]() 中的x和y都扩大2倍,则分式的值( )
中的x和y都扩大2倍,则分式的值( )
A.扩大4倍 B.扩大2倍 C.不变 D.缩小2倍
6.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣![]() x+b﹣l上,则常数b=( )
x+b﹣l上,则常数b=( )
A.![]() B.2 C.﹣1 D.1
B.2 C.﹣1 D.1
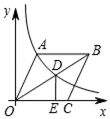
7.如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
A.1 B.![]() C.2
C.2![]() ﹣
﹣![]() D.
D.![]() ﹣1
﹣1
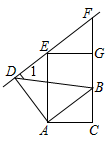
8.如图,线段![]() 由线段
由线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到,
得到,![]() 由
由![]() 沿
沿![]() 方向平移得到,且直线
方向平移得到,且直线![]() 过点
过点![]() .则
.则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
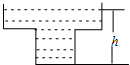
9.某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果以固定的流量把水蓄满蓄水池,下面的图象能大致表示水的深度h和注水时间t之间关系的是( )
A.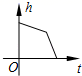 B.
B.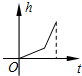
C.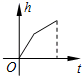 D.
D.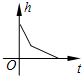
10.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠DEF的度数是( )
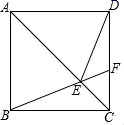
A.25° B.40° C.45° D.50°
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若三角形三边分别为6,8,10,那么它最长边上的中线长是_____.
12.一个多边形的各内角都相等,且内外角之差的绝对值为60°,则边数为__________.
13.某班有48名同学,在一次英语单词竞赛成绩统计中,成绩在81~ 90这一分数段的人数所占的频率是0.25,那么成绩在这个分数段的同学有_________名.
14.某校四个植树小队,在植树节这天种下柏树的棵数分别为10,x,10,8,若这组数据的中位数和平均数相等,那么x=_____.
15.在△ABC中,AB=![]() ,AC=5,若BC边上的高等于3,则BC边的长为_____.
,AC=5,若BC边上的高等于3,则BC边的长为_____.
16.已知:x=![]() ,y=
,y=![]() .那么
.那么![]() ______.
______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价.
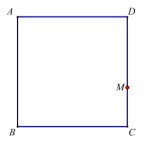
18.(8分)如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;②求证:BE⊥AC.
(2)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为 (直接写出答案).
19.(8分)一次函数图象经过(3,8)和(5,12)两点,求一次函数解析式.
20.(8分)解不等式组: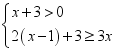 .并判断
.并判断![]() 这个数是否为该不等式组的解.
这个数是否为该不等式组的解.
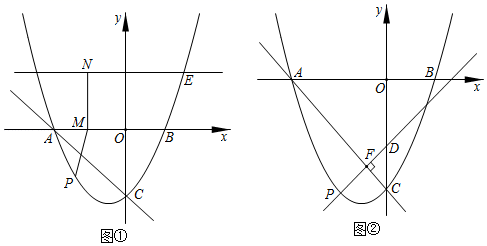
21.(8分)如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线上的点
,抛物线上的点![]() 的横坐标为3,过点
的横坐标为3,过点![]() 作直线
作直线![]() 轴.
轴.
(1)点![]() 为抛物线上的动点,且在直线
为抛物线上的动点,且在直线![]() 的下方,点
的下方,点![]() ,
,![]() 分别为
分别为![]() 轴,直线
轴,直线![]() 上的动点,且
上的动点,且![]() 轴,当
轴,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)过(1)中的点![]() 作
作![]() ,垂足为
,垂足为![]() ,且直线
,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕顶点
绕顶点![]() 旋转45°,得到
旋转45°,得到![]() ,再把
,再把![]() 沿直线
沿直线![]() 平移至
平移至![]() ,在平面上是否存在点
,在平面上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在直接写出点
为顶点的四边形为菱形?若存在直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
22.(10分)某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 150 | 200 | 350 | 400 | 450 | 500 |
优等品的频数m | 40 | 96 | 126 | 176 | 322 | 364 | 405 | 450 |
优等品的频率 | 0.80 | 0.96 | 0.84 |
| 0.92 |
| 0.90 |
|
(1)填写表中的空格;
(2)画出这批乒乓球优等品频率的折线统计图;
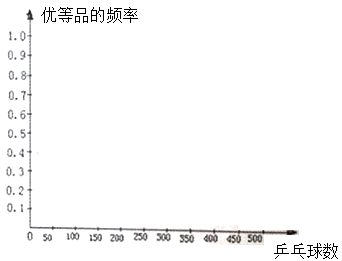
(3)这批乒乓球优等品概率的估计值是多少?
23.(10分)如图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC.(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结AE,交CD于点F,求证:△AFD ≌ △EFC.

24.(12分)如图,在ABCD中,AB∥CD,AD=BC,∠B=60°,AC平分∠DAB.
(1)求∠ACB的度数;
(2)如果AD=1,请直接写出向量![]() 和向量
和向量![]() 的模.
的模.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、A
4、C
5、B
6、B
7、C
8、B
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、3或1
13、1
14、12或1
15、9或1
16、98
三、解下列各题(本大题共8小题,共72分)
17、20元
18、(1)①见解析;②见解析;(2)![]()
19、y=1x+1.
20、![]() ,
, ![]() 不是不等式组的解.
不是不等式组的解.
21、(1)![]() (2)
(2)![]() ,
,![]() ,
,![]() ,
,![]()
22、(1)见解析;(2)见解析;(3)这批乒乓球优等品概率的估计值是0.90.
23、(1)作图解析;(2)证明见解析.
24、 (1)∠ACB=90°;(1)模分别为1和1.
2023-2024学年海南省农垦中学数学八上期末统考模拟试题含答案: 这是一份2023-2024学年海南省农垦中学数学八上期末统考模拟试题含答案,共7页。试卷主要包含了下列计算正确的是,下列命题是真命题的是,不等式组的非负整数解的个数是,已知,,是的三条边长,则的值是等内容,欢迎下载使用。
2023-2024学年海南省洋浦中学数学八上期末质量跟踪监视模拟试题含答案: 这是一份2023-2024学年海南省洋浦中学数学八上期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若三角形三个内角度数之比为2,若分式有意义,的值可以是,下列各式中,计算正确的是等内容,欢迎下载使用。
2022-2023学年湖北恩施龙凤民族初级中学数学七下期末统考模拟试题含答案: 这是一份2022-2023学年湖北恩施龙凤民族初级中学数学七下期末统考模拟试题含答案,共6页。试卷主要包含了若,则的值为,设,,则与的大小关系是等内容,欢迎下载使用。












