


2022-2023学年浙江省绍兴越城区五校联考数学七下期末达标检测试题含答案
展开2022-2023学年浙江省绍兴越城区五校联考数学七下期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设正比例函数y=mx的图象经过点A(m,4),且y的值随x的增大而增大,则m=( )
A.2 B.-2 C.4 D.-4
2.下列定理中,没有逆定理的是( )
A.两直线平行,同位角相等
B.全等三角形的对应边相等
C.全等三角形的对应角相等
D.在角的内部,到角的两边距离相等的点在角的平分线上
3.如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么![]() 的值为( )
的值为( )
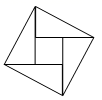
A.13 B.19 C.25 D.169
4.为了解我市八年级8000名学生期中数学考试情况,从中抽取了500名学生的数学成绩进行统计,下列说法正确的是( )
A.这种调查方式是普查 B.每名学生的数学成绩是个体
C.8000名学生是总体 D.500名学生是总体的一个样本
5.如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( )
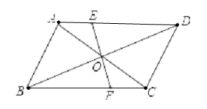
A.16 B.14 C.12 D.10
6.如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若点A(3,y1),B(﹣2,y2)都在直线y=﹣![]() x+n上,则y1与y2的大小关系是( )
x+n上,则y1与y2的大小关系是( )
A.y1<y2 B.y1>y2
C.y1=y2 D.以上都有可能
8.下列说法正确的是( )
A.某日最低气温是–2℃,最高气温是4℃,则该日气温的极差是2℃
B.一组数据2,2,3,4,5,5,5,这组数据的众数是2
C.小丽的三次考试的成绩是116分,120分,126分,则小丽这三次考试平均数是121分
D.一组数据2,2,3,4,这组数据的中位数是2.5
9.如图,一个函数的图象由射线![]() 、线段
、线段![]() 、射线
、射线![]() 组成,其中点
组成,其中点![]() ,
,![]() ,
,![]() ,
,![]() ,则此函数( )
,则此函数( )
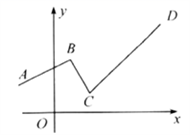
A.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
B.当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
C.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
10.下列方程中有实数根的是( )
A.![]() ; B.
; B.![]() =
=![]() ; C.
; C.![]() ; D.
; D.![]() =1+
=1+![]() .
.
11.某![]() 边形的每个外角都等于与它相邻内角的
边形的每个外角都等于与它相邻内角的![]() ,则
,则![]() 的值为( )
的值为( )
A.7 B.8 C.10 D.9
12.如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( )
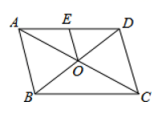
A.18 B.10 C.9 D.8
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.定义一种运算法则“![]() ”如下:
”如下:![]() ,例如:
,例如:![]() ,若
,若![]() ,则
,则![]() 的取值范围是____________.
的取值范围是____________.
14.某书定价25元,如果一次购买20本以上,超过20本的部分打八折,未超过20本的不打折,试写出付款金额![]() (单位:元)与购买数量
(单位:元)与购买数量![]() (单位:本)之间的函数关系_______.
(单位:本)之间的函数关系_______.
15.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买_____个.
16.使得二次根式![]() 有意义的x的取值范围是 .
有意义的x的取值范围是 .
17.计算:![]() =_____________。
=_____________。
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图,线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求线段
,求线段![]() 的长.
的长.
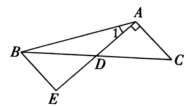
19.(5分)关于x的方程(2m+1)x2+4mx+2m﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数之和等于﹣1?若存在,求出m的值;若不存在,说明理由.
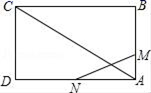
20.(8分)如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动.
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的![]() ?
?
(2)是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
21.(10分)(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| 空调 | 彩电 |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
22.(10分)为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.

23.(12分)某书店积极响应政府“改革创新,奋发有为”的号召,举办“读书节“系列活动.活动中故事类图书的标价是典籍类图书标价的1.5倍,若顾客用540元购买图书,能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本.
(1)求活动中典籍类图书的标价;
(2)该店经理为鼓励广大读者购书,免费为购买故事类的读者赠送图1所示的精致矩形包书纸.在图1的包书纸示意图中,虚线是折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长为折叠进去的宽度.已知该包书纸的面积为875cm2(含阴影部分),且正好可以包好图2中的《中国故事》这本书,该书的长为21cm,宽为15cm,厚为1cm,请直接写出该包书纸包这本书时折叠进去的宽度.

参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、C
3、C
4、B
5、C
6、A
7、A
8、D
9、A
10、B
11、C
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、![]()
15、1
16、x≥﹣![]()
17、2+![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、![]()
19、(1)m>﹣![]() 且m≠﹣
且m≠﹣![]() ;(2)不存在.理由见解析.
;(2)不存在.理由见解析.
20、(1)1秒或2秒,(2)存在,![]() 秒或
秒或![]() 秒
秒
21、解:(1)设商场计划购进空调x台,则计划购进彩电(30﹣x)台,由题意,得
y=(6100﹣5400)x+(3900﹣3500)(30﹣x)=300x+12000。
(2)依题意,得![]() ,
,
解得10≤x≤![]() 。
。
∵x为整数,∴x=10,11,12。∴商场有三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台。
(3)∵y=300x+12000,k=300>0,∴y随x的增大而增大。
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元。
22、(1)7,1.4,2.1;(2)y1=2.1x﹣0.3;图象见解析;(3)函数y1与y2的图象存在交点(![]() ,9);其意义为当 x<
,9);其意义为当 x<![]() 时是方案调价前合算,当x>
时是方案调价前合算,当x>![]() 时方案调价后合算.
时方案调价后合算.
23、(1)典籍类图书的标价为1元;(2)折叠进去的宽度为2cm
浙江省绍兴市越城区五校联考2023-2024学年数学九上期末考试模拟试题含答案: 这是一份浙江省绍兴市越城区五校联考2023-2024学年数学九上期末考试模拟试题含答案,共8页。
2023-2024学年浙江省绍兴越城区五校联考数学八年级第一学期期末复习检测试题含答案: 这是一份2023-2024学年浙江省绍兴越城区五校联考数学八年级第一学期期末复习检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列各式中,正确的是,已知,则M等于等内容,欢迎下载使用。
浙江省绍兴市越城区五校联考2023-2024学年数学八上期末监测试题含答案: 这是一份浙江省绍兴市越城区五校联考2023-2024学年数学八上期末监测试题含答案,共7页。试卷主要包含了下列运算正确的是等内容,欢迎下载使用。












