2022-2023学年浙江省金华婺城区四校联考七年级数学第二学期期末调研模拟试题含答案

这是一份2022-2023学年浙江省金华婺城区四校联考七年级数学第二学期期末调研模拟试题含答案，共7页。试卷主要包含了下列事件中，属于随机事件的是，如果关于x的一次函数y＝，已知直线，则关于x的方程的解为，若，则下列各式中，错误的是等内容，欢迎下载使用。
2022-2023学年浙江省金华婺城区四校联考七年级数学第二学期期末调研模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题(每小题3分,共30分)1．下列多项式中，不是完全平方式的是　　A． B． C． D．2．下列计算中正确的是（     ）A． B． C． D．3．如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为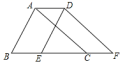（　　）A．8 B．10 C．12 D．144．下列事件中，属于随机事件的是（    ）．A．凸多边形的内角和为B．凸多边形的外角和为C．四边形绕它的对角线交点旋转能与它本身重合D．任何一个三角形的中位线都平行于这个三角形的第三边5．如图，△ABC中，AB=AC=15，AD平分∠BAC，点E为AC的中点，连接DE，若△CDE的周长为21，则BC的长为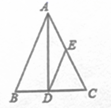（    ）A．16 B．14 C．12 D．66．如果关于x的一次函数y＝（a+1）x+（a﹣4）的图象不经过第二象限，且关于x的分式方程有整数解，那么整数a值不可能是（  ）A．0 B．1 C．3 D．47．为了保障艺术节表演的整体效果，某校在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示点A的坐标为，表示点B的坐标为，则表示其他位置的点的坐标正确的是（    ）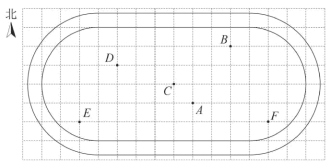A． B． C． D．8．已知直线（m，n为常数）经过点（0，-4）和（3，0），则关于x的方程的解为A． B． C． D．9．如图，正方形的对角线是菱形的一边，则等于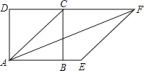（ ）A．135° B．45° C．22.5° D．30°10．若，则下列各式中，错误的是（　　）A． B． C． D．二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，甲、乙两名同学分别站在C、D的位置时，乙的影子与甲的影子的末端恰好在同一点，已知甲、乙两同学相距1m，甲身高1.8m，乙身高1.5m，则甲的影子是________m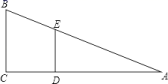．12．若关于的分式方程有解,则的取值范围是_______.13．当__________时，代数式取得最小值．14．如图，矩形ABCD中，，，CB在数轴上，点C表示的数是，若以点C为圆心，对角线CA的长为半径作弧交数轴的正半轴于点P，则点P表示的数是______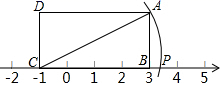．15．如图，将三角形纸片的一角折叠，使点B落在AC边上的F处，折痕为DE．已知AB＝AC＝3，BC＝4，若以点E，F，C为顶点的三角形与△ABC相似，那么BE的长是_______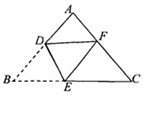．16．如图，是六边形的一个内角.若，则的度数为________.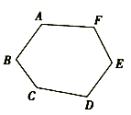三、解下列各题(本大题共8小题，共72分)17．（8分）求证：三角形的一条中位线与第三边上的中线互相平分．要求：(1)根据给出的和它的一条中位线,在给出的图形上,请用尺规作出边上的中线,交于点．不写作法,保留痕迹；(2)据此写出已知,求证和证明过程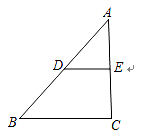．   18．（8分）为了普及环保知识，增强环保意识，某大学某专业学院从本专业450人中随机抽取了30名学生参加环保知识测试，得分（十分制）情况如图所示：（1）这30名学生的测试成绩的众数，中位数，平均数分别是多少？（2）学院准备拿出2000元购买奖品奖励测试成绩优秀的学生，奖品分为三等，成绩为10分的为一等，成绩为8分和9分的为二等，成绩为7分的为三等；学院要求一等奖奖金，二等奖奖金，三等奖奖金分别占20%、40%、40%，问每种奖品的单价各为多少元？（3）如果该专业学院的学生全部参加测试，在（2）问的奖励方案下，请你预测该专业学院将会拿出多少奖金来奖励学生，其中一等奖奖金为多少元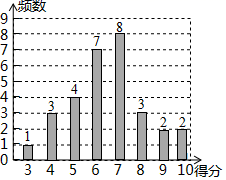？   19．（8分）操作与证明：如图，把一个含角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AC、AE、其中AC与EF交于点N，取AF中点M，连接MD、MN．求证：是等腰三角形；在的条件下，请判断MD，MN的数量关系和位置关系，并给出证明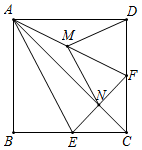．   20．（8分）在正方形ABCD中，点E是射线AC上一点，点F是正方形ABCD外角平分线CM上一点，且CF=AE，连接BE，EF.(1)如图1，当E是线段AC的中点时，直接写出BE与EF的数量关系；(2)当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断(1)中的结论是否成立，并证明你的结论；(3)当点B，E，F在一条直线上时，求∠CBE的度数.(直接写出结果即可) 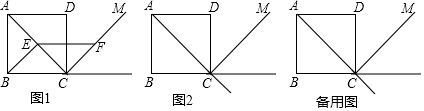  21．（8分）如图，Rt△ABO的顶点A是双曲线y1＝与直线y2＝－x-(k+1)在第二象限的交点.AB⊥x轴于B，且S△ABO＝．（1）求这两个函数的解析式；（2）求△AOC的面积．（3）直接写出使y1＞y2成立的x的取值范围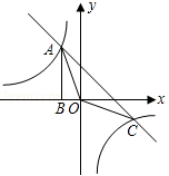   22．（10分）水果批发市场有一种高档水果，如果每千克盈利（毛利润）10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销量将减少20千克.（1）若以每千克能盈利18元的单价出售，问每天的总毛利润为多少元？ （2）现市场要保证每天总毛利润6000元，同时又要使顾客得到实惠，则每千克应涨价多少元？   23．（10分）如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣1，1），B（﹣3，1），C（﹣1，4）．（1）画出△ABC关于y轴对称的△A1B1C1；（1）将△ABC绕着点B顺时针旋转90°后得到△A1BC1，请在图中画出△A1BC1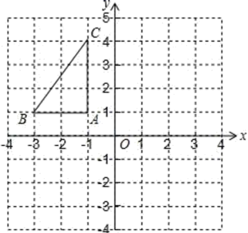．   24．（12分） “书香校园”活动中，某校同时购买了甲、乙两种图书，已知两种图书的购书款均为360元，甲种图书的单价比乙种图书低50%，甲种图书比乙种图书多4本，甲、乙两种图书的单价分别为多少元？   参考答案 一、选择题(每小题3分,共30分)1、D2、A3、C4、C5、C6、B7、B8、C9、C10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、13、14、15、或1．16、 三、解下列各题(本大题共8小题，共72分)17、 (1)作线段的中段线,的中点为,连结即可,见解析；(2) 见解析.18、（1）众数是7，中位数是 7，平均数是，（2）一，二，三等奖奖金每种奖品的单价分别为200元，160元，100元；（3）一等奖奖金为6000元．19、（1）证明见解析；（2）20、（1）EF=BE；（2）EF=BE，理由见解析；（3）当B，E，F在一条直线上时，∠CBE=22.5°21、（1）y=﹣，y=﹣x+2；（2）3；（1）-1＜x＜0或x＞122、（1）6120元  （2）答应涨价为5元.23、 (1)见解析.(1)见解析.24、甲种图书的单价为每本45元，乙种图书的单价为每本90元