


2022-2023学年湖北省孝感市数学七年级第二学期期末调研模拟试题含答案
展开
这是一份2022-2023学年湖北省孝感市数学七年级第二学期期末调研模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
2022-2023学年湖北省孝感市数学七年级第二学期期末调研模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )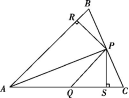 A.①② B.②③ C.①③ D.①②③2.如图,在△ABC中,DE∥BC,若
A.①② B.②③ C.①③ D.①②③2.如图,在△ABC中,DE∥BC,若![]() =
=![]() ,则
,则![]() 的值为( )
的值为( )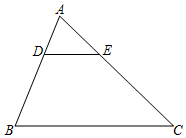 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )A.2 B.3 C.
3.在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )A.2 B.3 C.![]() D.54.如图,若正比例函数y=kx图象与四条直线x=1,x=2,y=1,y=2相交围成的正方形有公共点,则k的取值范围是( )
D.54.如图,若正比例函数y=kx图象与四条直线x=1,x=2,y=1,y=2相交围成的正方形有公共点,则k的取值范围是( )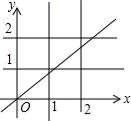 A.k≤2 B.k≥
A.k≤2 B.k≥![]() C.0<k<
C.0<k<![]() D.
D.![]() ≤k≤25.小华的爷爷每天坚持体育锻炼,某天他慢跑从家到中山公园,打了一会儿太极拳后坐公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图像是( ).A.
≤k≤25.小华的爷爷每天坚持体育锻炼,某天他慢跑从家到中山公园,打了一会儿太极拳后坐公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图像是( ).A.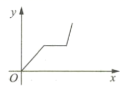 B.
B.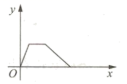 C.
C.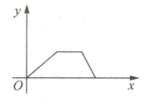 D.
D.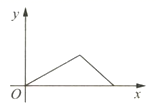 6.京剧是中国的“国粹”,京剧脸谱是一种具有汉族文化特色的特殊化妆方法
6.京剧是中国的“国粹”,京剧脸谱是一种具有汉族文化特色的特殊化妆方法![]() 由于每个历史人物或某一种类型的人物都有一种大概的谱式,就像唱歌、奏乐都要按照乐谱一样,所以称为“脸谱”
由于每个历史人物或某一种类型的人物都有一种大概的谱式,就像唱歌、奏乐都要按照乐谱一样,所以称为“脸谱”![]() 如图是京剧
如图是京剧![]() 华容道
华容道![]() 中关羽的脸谱图案
中关羽的脸谱图案![]() 在下面的四个图案中,可以通过平移图案得到的是
在下面的四个图案中,可以通过平移图案得到的是![]()
![]()
 A.
A. B.
B. C.
C. D.
D. 7.如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )
7.如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )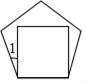 A.30° B.15° C.18° D.20°8.下列等式从左到右的变形,属于因式分解的是( )A.
A.30° B.15° C.18° D.20°8.下列等式从左到右的变形,属于因式分解的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
9.如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )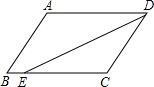 A.2cm B.4cm C.6cm D.8cm10.如图,菱形ABCD中,AB=4,E,F分别是AB、BC的中点,P是AC上一动点,则PF+PE的最小值是( )
A.2cm B.4cm C.6cm D.8cm10.如图,菱形ABCD中,AB=4,E,F分别是AB、BC的中点,P是AC上一动点,则PF+PE的最小值是( )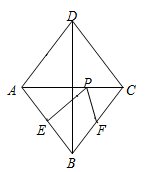 A.3 B.
A.3 B.![]() C.4 D.
C.4 D.![]() 11.当x分别取-2019、-2018、-2017、…、-2、-1、0、1、
11.当x分别取-2019、-2018、-2017、…、-2、-1、0、1、![]() 、
、![]() 、…、
、…、![]() 、
、![]() 、
、![]() 时,分别计算分式
时,分别计算分式![]() 的值,再将所得结果相加,其和等于( )A.-1 B.1 C.0 D.201912.如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )
的值,再将所得结果相加,其和等于( )A.-1 B.1 C.0 D.201912.如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )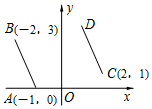 A..(1,4) B..(1,3) C..(2,4) D..(2,3)二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数
A..(1,4) B..(1,3) C..(2,4) D..(2,3)二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数![]() 的自变量的取值范围是
的自变量的取值范围是![]() .14.已知点
.14.已知点![]() 及第二象限的动点
及第二象限的动点![]() ,且
,且![]() .设
.设![]() 的面积为
的面积为![]() ,则
,则![]() 关于
关于![]() 的函数关系式为________.15.
的函数关系式为________.15.![]() ______.16.如图,在等腰直角三角形ACD,∠ACD=90°,AC=
______.16.如图,在等腰直角三角形ACD,∠ACD=90°,AC=![]() ,分别以边AD,AC,CD为直径面半图,所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)为_____________.
,分别以边AD,AC,CD为直径面半图,所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)为_____________.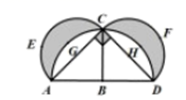 17.甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是
17.甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是![]() ,则成绩比较稳定的是 (填“甲”或“乙”)三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题:
,则成绩比较稳定的是 (填“甲”或“乙”)三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题: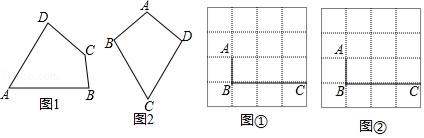 (1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °(2)在探究等对角四边形性质时:小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长. 19.(5分)某工厂制作AB两种型号的环保包装盒.已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个,且制作一个A型盒比制作一个B型盒要多用20%的材料.求制作每个A,B型盒各用多少材料? 20.(8分)如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °(2)在探究等对角四边形性质时:小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长. 19.(5分)某工厂制作AB两种型号的环保包装盒.已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个,且制作一个A型盒比制作一个B型盒要多用20%的材料.求制作每个A,B型盒各用多少材料? 20.(8分)如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=![]() 的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).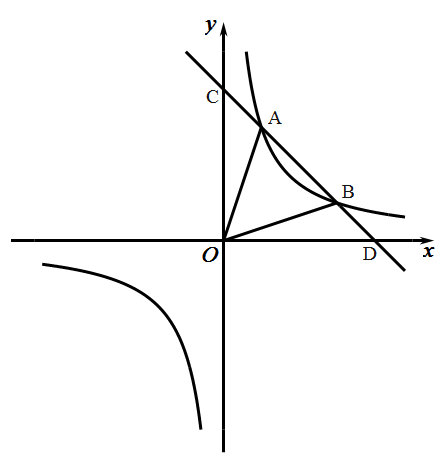 (1)求一次函数与反比例函数的解析式;(2)求C、D两点的坐标,并求△AOB的面积;(3)根据图象直接写出:当x在什么取值范围时,y1>y2? 21.(10分)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
(1)求一次函数与反比例函数的解析式;(2)求C、D两点的坐标,并求△AOB的面积;(3)根据图象直接写出:当x在什么取值范围时,y1>y2? 21.(10分)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F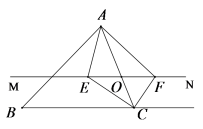 (1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论. 22.(10分)如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系?若存在,证明你的结论;若不存在,请说明理由.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论. 22.(10分)如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系?若存在,证明你的结论;若不存在,请说明理由.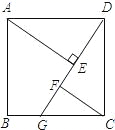 23.(12分)无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:(1)水蜜桃进价为每箱多少元?(2)乙超市获利多少元?哪种销售方式更合算? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、C4、D5、C6、A7、C8、B9、A10、C11、A12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、x≠114、
23.(12分)无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:(1)水蜜桃进价为每箱多少元?(2)乙超市获利多少元?哪种销售方式更合算? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、C4、D5、C6、A7、C8、B9、A10、C11、A12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、x≠114、![]()
![]() 15、
15、![]() 16、117、甲 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)140°,1°;(2)证明见解析;(3)见解析;(4)2
16、117、甲 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)140°,1°;(2)证明见解析;(3)见解析;(4)2![]() 或2
或2![]() .19、制作每个A型盒用0.1米材料,制作每个B型盒用0.5米材料.20、(1)y1=
.19、制作每个A型盒用0.1米材料,制作每个B型盒用0.5米材料.20、(1)y1=![]() ,y1=﹣x+4;(1)4;(3)当 x 满足 1<x<3 、x<2时,则 y1>y1.21、 (1)见解析;(2) 当O运动到OA=OC处,四边形AECF是矩形.理由见解析.22、AE=FC+EF,证明见解析.23、 (1)水蜜桃进价为每箱100元; (2)乙超市获利为33000元,甲种销售方式获利多.
,y1=﹣x+4;(1)4;(3)当 x 满足 1<x<3 、x<2时,则 y1>y1.21、 (1)见解析;(2) 当O运动到OA=OC处,四边形AECF是矩形.理由见解析.22、AE=FC+EF,证明见解析.23、 (1)水蜜桃进价为每箱100元; (2)乙超市获利为33000元,甲种销售方式获利多.
相关试卷
这是一份湖北省孝感市孝南区八校2022-2023学年七下数学期末调研试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
这是一份湖北省孝感市孝南区2022-2023学年数学七年级第二学期期末调研模拟试题含答案,共7页。试卷主要包含了若x=1,则x的值是,不等式的解集是,下列各式的计算中,正确的是等内容,欢迎下载使用。
这是一份湖北省孝感市名校2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列函数中,正比例函数是等内容,欢迎下载使用。









