2022-2023学年湖北省武汉市部分重点学校七下数学期末复习检测试题含答案

2022-2023学年湖北省武汉市部分重点学校七下数学期末复习检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（　　）

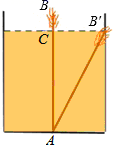
A．15尺 B．16尺 C．17尺 D．18尺

2．在，，，高，则BC的长是（  ）

A．14 B．4 C．4或14 D．7或13

3．把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是（　　）

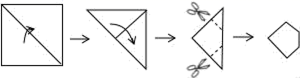
A．六边形 B．八边形 C．十二边形 D．十六边形

4．如果一个多边形的内角和是外角和的3倍，那么这个多边形是（  ）

A．四边形 B．六边形 C．八边形 D．十边形

5．如图，大正方形与小正方形的面积之差是40，则阴影部分的面积是(     )

A．80 B．40 C．20 D．10

6．7 的小数部分是（    ）

A．4 - B．3  C．4  D．3 

7．函数中自变量x的取值范围是(　　　　)

A． B． C． D．

8．等腰三角形的底边和腰长分别是10和12，则底边上的高是（    ）

A．13 B．8 C． D．

9．如图，在方格中有两个涂有阴影的图形M、N，每个小正方形的边长都是1个单位长度，图（1）中的图形M平移后位置如图（2）所示，以下对图形M的平移方法叙述正确的是（    ）

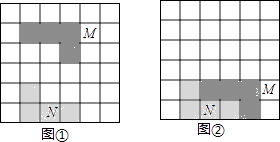
A．先向右平移2个单位长度，再向下平移3个单位长度

B．先向右平移1个单位长度，再向下平移3个单位长度

C．先向右平移1个单位长度，再向下平移4个单位长度

D．先向右平移2个单位长度，再向下平移4个单位长度

10．已知：，计算：的结果是（）

A． B． C． D．

11．方程x2﹣4x+5＝0根的情况是（　　）

A．有两个不相等的实数根 B．有两个相等的实数根

C．有一个实数根 D．没有实数根

12．无理数在两个整数之间，下列结论正确的是（    ）

A．2~3之间 B．3~4之间 C．4~5之间 D．5~6之间

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，已知一次函数与一次函数的图像相交于点P（-2,1），则关于不等式x+b≥mx-n的解集为_____.

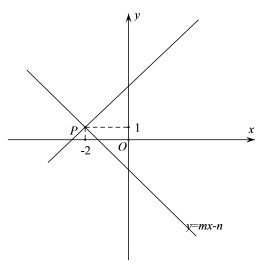
14．已知函数，当时，函数值为______．

15．要使分式的值为0，则x的值为____________．

16．一个两位数，它的十位数上的数字比个位上的数字大2.且这个两位数小于40，则这个两位数是________.

17．一组数据 ，则这组数据的方差是 __________ .

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）．

19．（5分）先化简，再求值：当a=7时，求a+的值．

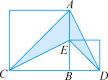
20．（8分）如图，在平面直角坐标系xOy中，点A的坐标为（－2，0），等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD．

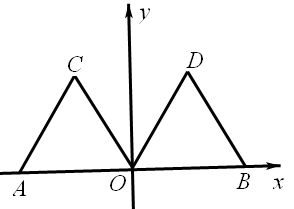
（1）△AOC沿x轴向右平移得到△OBD，则平移的距离是       个单位长度；△AOC与△OBD关于直线对称，则对称轴是       ；△AOC绕原点O顺时针旋转得到△OBD，则旋转角可以是       度；

（2）连接AD，交OC于点E，求∠AEO的度数.

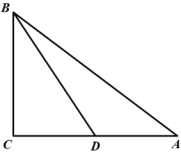
21．（10分）如图，△ABC中，AB=10，BC=6，AC=8.

（1）求证：△ABC是直角三角形；

（2）若D是AC的中点，求BD的长.（结果保留根号）

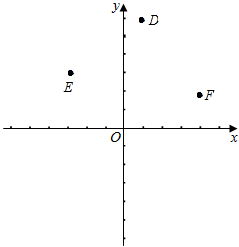
22．（10分）阅读下列一段文字，然后回答下列问题．

已知在平面内有两点、，其两点间的距离，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可化简为或.

（1）已知、，试求A、B两点间的距离______.

已知M、N在平行于y轴的直线上，点M的纵坐标为4，点N的纵坐标为-1，试求M、N两点的距离为______；

（2）已知一个三角形各顶点坐标为、、，你能判定此三角形的形状吗?说明理由．

（3）在（2）的条件下，平面直角坐标系中，在x轴上找一点P，使的长度最短，求出点P的坐标及的最短长度．

23．（12分）某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元．

（1）求A型空调和B型空调每台各需多少元；

（2）若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？

（3）在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、C

3、B

4、C

5、C

6、A

7、B

8、D

9、B

10、C

11、D

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、5

15、-2.

16、31或1

17、1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、

19、，13

20、（1）2；y轴；120（2）90°

21、 (1)见解析;(2)2.

22、（1）13，5；（2）等腰直角三角形，理由见解析；（3）当P的坐标为（）时，PD+PF的长度最短，最短长度为.

23、（1）A型空调和B型空调每台各需9000元、6000元；（2）共有三种采购方案，方案一：采购A型空调10台，B型空调20台，方案二：采购A型空调11台，B型空调19台，案三：采购A型空调12台，B型空调18台；（3）采购A型空调10台，B型空调20台可使总费用最低，最低费用是210000元．