


2022-2023学年湖南省湘西土家族苗族自治州凤凰县七年级数学第二学期期末教学质量检测模拟试题含答案
展开
这是一份2022-2023学年湖南省湘西土家族苗族自治州凤凰县七年级数学第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了下列命题中,真命题是,一元二次方程 x2= x的根是等内容,欢迎下载使用。
2022-2023学年湖南省湘西土家族苗族自治州凤凰县七年级数学第二学期期末教学质量检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗. 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.点![]() ,点
,点![]() 是一次函数
是一次函数![]() 图象上的两个点,且
图象上的两个点,且![]() ,则
,则![]() 与
与![]() 的大小关系是( )A.
的大小关系是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.如图,直线
2.如图,直线![]() 经过点A(a,
经过点A(a,![]() )和点B(
)和点B(![]() ,0),直线
,0),直线![]() 经过点A,则当
经过点A,则当![]() 时,x的取值范围是( )
时,x的取值范围是( )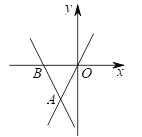 A.x>-1 B.x<-1 C.x>-2 D.x<-23.甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
A.x>-1 B.x<-1 C.x>-2 D.x<-23.甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示: 甲乙丙丁平均数
与方差s2如下表所示: 甲乙丙丁平均数![]() (cm)561560561560方差s23.53.515.516.5根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A.甲 B.乙 C.丙 D.丁4.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
(cm)561560561560方差s23.53.515.516.5根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A.甲 B.乙 C.丙 D.丁4.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子![]() (x>0)的最小值是1”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是1”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是![]() ,矩形的周长是1(
,矩形的周长是1(![]() );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=![]() (x>0),解得x=1,这时矩形的周长1(
(x>0),解得x=1,这时矩形的周长1(![]() )=4最小,因此
)=4最小,因此![]() (x>0)的最小值是1.模仿张华的推导,你求得式子
(x>0)的最小值是1.模仿张华的推导,你求得式子![]() (x>0)的最小值是( )A.1 B.1 C.6 D.105.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(-2,1),则点B的对应点B1的坐标为( )A.(2,-1) B.(2,1) C.(﹣2,-1) D.(1,2)6.如图,矩形纸片
(x>0)的最小值是( )A.1 B.1 C.6 D.105.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(-2,1),则点B的对应点B1的坐标为( )A.(2,-1) B.(2,1) C.(﹣2,-1) D.(1,2)6.如图,矩形纸片![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的长等于( )
的长等于( )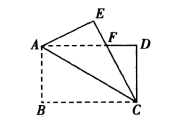 A.
A.![]() B.
B.![]() C.
C.![]() D.7.下列命题中,真命题是( )A.相等的角是直角B.不相交的两条线段平行C.两直线平行,同位角互补D.经过两点有且只有一条直线8.一元二次方程 x2= x的根是( )A.
D.7.下列命题中,真命题是( )A.相等的角是直角B.不相交的两条线段平行C.两直线平行,同位角互补D.经过两点有且只有一条直线8.一元二次方程 x2= x的根是( )A.![]() =0,
=0,![]() =1 B.
=1 B.![]() =0,
=0,![]() =-1 C.
=-1 C.![]() =
=![]() =0 D.
=0 D.![]() =
=![]() =19.在下列四组数中,不是勾股数的一组数是( )A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=710.已知一次函数y=ax+b(a≠0,a,b为常数),x与y的对应值如表:x﹣10123y3210﹣1不等式ax+b<0的解集是( )A.x>﹣2 B.x<2 C.x>0 D.x>211.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
=19.在下列四组数中,不是勾股数的一组数是( )A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=710.已知一次函数y=ax+b(a≠0,a,b为常数),x与y的对应值如表:x﹣10123y3210﹣1不等式ax+b<0的解集是( )A.x>﹣2 B.x<2 C.x>0 D.x>211.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )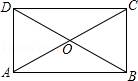 A.2 B.4 C.
A.2 B.4 C.![]() D.
D.![]() 12.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是
12.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是![]()
![]() A.平均数 B.中位数 C.众数 D.方差二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图是甲、乙两射击运动员的10次射击训练成绩的折射线统计图,则射击成绩较稳定的是__________(填“甲”或“乙”)。
A.平均数 B.中位数 C.众数 D.方差二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图是甲、乙两射击运动员的10次射击训练成绩的折射线统计图,则射击成绩较稳定的是__________(填“甲”或“乙”)。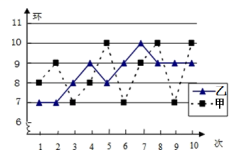 14.如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=
14.如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=![]() ;再过P1作P1P2⊥OP1且P1P2=1,得OP2=
;再过P1作P1P2⊥OP1且P1P2=1,得OP2=![]() ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得
;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得![]() =____.
=____.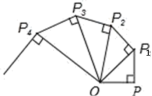 15.如图是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…,依此类推,若正方形①的边长为64cm,则正方形⑦的边长为 cm.
15.如图是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…,依此类推,若正方形①的边长为64cm,则正方形⑦的边长为 cm.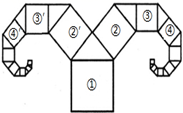 16.如果关于x的方程kx2﹣6x+9=0有两个相等的实数根,那么k的值为_____.17.如图,点P是平面坐标系中一点,则点P到原点的距离是_____.
16.如果关于x的方程kx2﹣6x+9=0有两个相等的实数根,那么k的值为_____.17.如图,点P是平面坐标系中一点,则点P到原点的距离是_____. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.(1)求证:△AEB≌△CFD;(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.(1)求证:△AEB≌△CFD;(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.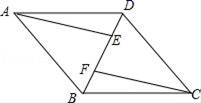 19.(5分)如图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,求证:FG⊥DE.
19.(5分)如图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,求证:FG⊥DE.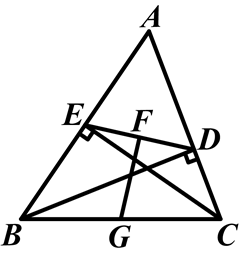 20.(8分)如图,点E,F为▱ABCD的对角线BD上的两点,连接AE,CF,∠AEB=∠CFD.求证:AE=CF.
20.(8分)如图,点E,F为▱ABCD的对角线BD上的两点,连接AE,CF,∠AEB=∠CFD.求证:AE=CF.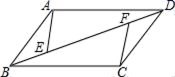 21.(10分)有两堆背面完全相同的扑克,第一堆正面分别写有数字1、2、1、4,第二堆正面分别写有数字1、2、1.分别混合后,小玲从第一堆中随机抽取一张,把卡片上的数字作为被减数;小惠从第二堆中随机抽取一张,把卡片上的数字作为减数,然后计算出这两个数的差.(1)请用画树状图或列表的方法,求这两数差为0的概率;(2)小玲与小惠作游戏,规则是:若这两数的差为非负数,则小玲胜;否则,小惠胜.你认为该游戏规则公平吗?如果公平,请说明理由.如果不公平,请你修改游戏规则,使游戏公平. 22.(10分)如图1,已知AB⊥CD,C是AB上一动点,AB=CD(1)在图1中,将BD绕点B逆时针方向旋转90°到BE,若连接DE,则△DBE为等腰直角三角形;若连接AE,试判断AE与BC的数量和位置关系并证明;(2)如图2,F是CD延长线上一点,且DF=BC,直线AF,BD相交于点G,∠AGB的度数是一个固定值吗?若是,请求出它的度数;若不是,请说明理由.
21.(10分)有两堆背面完全相同的扑克,第一堆正面分别写有数字1、2、1、4,第二堆正面分别写有数字1、2、1.分别混合后,小玲从第一堆中随机抽取一张,把卡片上的数字作为被减数;小惠从第二堆中随机抽取一张,把卡片上的数字作为减数,然后计算出这两个数的差.(1)请用画树状图或列表的方法,求这两数差为0的概率;(2)小玲与小惠作游戏,规则是:若这两数的差为非负数,则小玲胜;否则,小惠胜.你认为该游戏规则公平吗?如果公平,请说明理由.如果不公平,请你修改游戏规则,使游戏公平. 22.(10分)如图1,已知AB⊥CD,C是AB上一动点,AB=CD(1)在图1中,将BD绕点B逆时针方向旋转90°到BE,若连接DE,则△DBE为等腰直角三角形;若连接AE,试判断AE与BC的数量和位置关系并证明;(2)如图2,F是CD延长线上一点,且DF=BC,直线AF,BD相交于点G,∠AGB的度数是一个固定值吗?若是,请求出它的度数;若不是,请说明理由.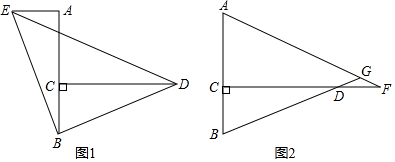 23.(12分)如图,E与F分别在正方形ABCD边BC与CD上,∠EAF=45°.(1)以A为旋转中心,将△ABE按顺时针方向旋转90°,画出旋转后得到的图形.(2)已知BE=2cm,DF=3cm,求EF的长.
23.(12分)如图,E与F分别在正方形ABCD边BC与CD上,∠EAF=45°.(1)以A为旋转中心,将△ABE按顺时针方向旋转90°,画出旋转后得到的图形.(2)已知BE=2cm,DF=3cm,求EF的长.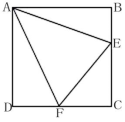 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、A3、A4、C5、A6、B7、D8、A9、D10、D11、B12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、乙14、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、A3、A4、C5、A6、B7、D8、A9、D10、D11、B12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、乙14、![]() 15、816、1.17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)证明见解析.19、如图,连接EG,DG.∵CE是AB边上的高,∴CE⊥AB.在Rt△CEB中,G是BC的中点,∴
15、816、1.17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)证明见解析.19、如图,连接EG,DG.∵CE是AB边上的高,∴CE⊥AB.在Rt△CEB中,G是BC的中点,∴![]() .同理,
.同理,![]() .∴EG=DG.又∵F是ED的中点,∴FG⊥DE.
.∴EG=DG.又∵F是ED的中点,∴FG⊥DE.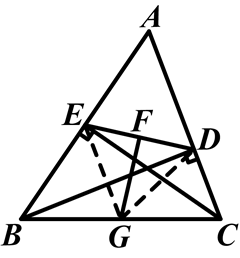 20、详见解析21、(1)表见解析,
20、详见解析21、(1)表见解析,![]() ;(2)不公平,修改规则为:两数的差为正数,则小玲胜;否则,小惠胜.(规则不唯一)22、(1)AE=BC,AE⊥BC,证明见解析;(2)∠AGB的度数是固定值,度数为45°.23、(1)见解析;(2)5cm.
;(2)不公平,修改规则为:两数的差为正数,则小玲胜;否则,小惠胜.(规则不唯一)22、(1)AE=BC,AE⊥BC,证明见解析;(2)∠AGB的度数是固定值,度数为45°.23、(1)见解析;(2)5cm.
相关试卷
这是一份2023-2024学年湖南省湘西土家族苗族自治州凤凰县九上数学期末达标测试试题含答案,共8页。试卷主要包含了将两个圆形纸片,点M关于原点对称的点N的坐标是,二次三项式配方的结果是等内容,欢迎下载使用。
这是一份2023-2024学年湖南省湘西土家族苗族自治州凤凰县数学九年级第一学期期末教学质量检测试题含答案,共8页。试卷主要包含了下列事件是随机事件的是,下列图案中,是中心对称图形的是,下列运算中,结果正确的是等内容,欢迎下载使用。
这是一份2023-2024学年湖南省凤凰县九上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了一元二次方程的解为等内容,欢迎下载使用。









