2022-2023学年江苏省泰兴市老叶初级中学数学七年级第二学期期末学业水平测试模拟试题含答案

2022-2023学年江苏省泰兴市老叶初级中学数学七年级第二学期期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．当1＜a＜2时，代数式＋|1－a|的值是(     )

A．－1 B．1 C．2a－3 D．3－2a

2．在正方形中，是边上一点，若，且点与点不重合，则的长可以是（      ）

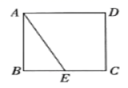
A．3 B．4 C．5 D．6

3．如图，在长方形纸片中，，.点是的中点，点是边上的一个动点.将沿所在直线翻折，得到.则长的最小值是（   ）

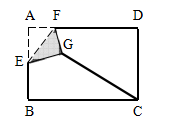
A． B． C． D．

4．10名学生的平均成绩是x，如果另外5名学生每人得90分，那么整个组的平均成绩是（　　）

A． B． C． D．

5．如图，在平行四边形ABCD中，DE平分∠ADC交BC于E，AF⊥DE，垂足为F，已知∠DAF＝50°，则∠B＝（　　）

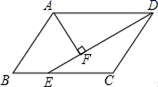
A．50° B．40° C．80° D．100°

6．在平面直角坐标系中，将直线l1：y＝－3x－2向左平移1个单位，再向上平移3个单位得到直线l2，则直线l2的解析式为(　　)

A．y＝－3x－9 B．y＝－3x－2

C．y＝－3x＋2 D．y＝－3x＋9

7．  如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（　　）

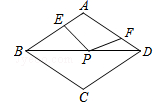
A．1 B．2 C．3 D．4

8．下列多项式中，能用完全平方公式因式分解的是（     ）

A．m2   mn n2 B．x2 y2   2xy

C．a2   2a  D．n2   2n  4

9．菱形的对角线长分别为6和8，则该菱形的面积是（    ）

A．24 B．48 C．12 D．10

10．分式①，②，③，④中，最简分式有(　　)

A．1个 B．2个 C．3个 D．4个

二、填空题(本大题共有6小题，每小题3分，共18分)

11．直线与轴、轴的交点分别为、则这条直线的解析式为__________．

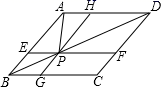
12．如图，平行四边形ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，且CG=2BG，连接AP，若S△APH=2，则S四边形PGCD=______．

13．如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为________.

14．化简：的结果是________.

15．2018年6月1日，美国职业篮球联赛（NBA）总决赛第一场在金州勇士队甲骨文球馆进行．据统计，当天通过腾讯视频观看球赛的人数突破5250万．用科学记数法表示“5250”为_____．

16．因式分解:_________

三、解下列各题(本大题共8小题，共72分)

17．（8分）在▱ABCD中，点E、F分别在AB、CD上，且AE=CF．

（1）求证：△ADE≌△CBF；

（2）若DF=BF，求证：四边形DEBF为菱形．

18．（8分）先化简再求值

，其中.

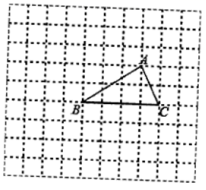
19．（8分）如图所示，在边长为1个单位长度的小正方形组成的网格中，的顶点A、B、C在格点（网格线的交点）上．

（1）将绕点B逆时针旋转，得到，画出；

（2）以点A为位似中心放大，得到，使放大前后的三角形面积之比为1:4，请你在网格内画出．

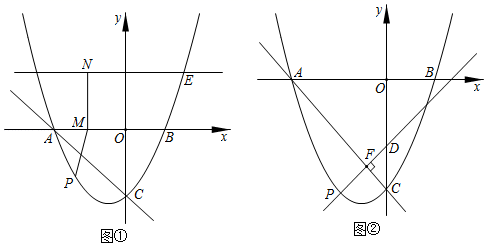
20．（8分）如图，抛物线与轴交于， （在的左侧），与轴交于点，抛物线上的点的横坐标为3，过点作直线轴．

（1）点为抛物线上的动点，且在直线的下方，点，分别为轴，直线上的动点，且轴，当面积最大时，求的最小值；

（2）过（1）中的点作，垂足为，且直线与轴交于点，把绕顶点旋转45°，得到，再把沿直线平移至，在平面上是否存在点，使得以，，，为顶点的四边形为菱形？若存在直接写出点的坐标；若不存在，说明理由．

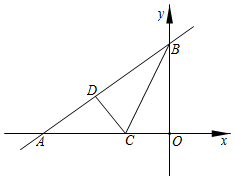
21．（8分）已知：直线y＝与x轴、y轴分别相交于点A和点B，点C在线段AO上．将△CBO沿BC折叠后，点O恰好落在AB边上点D处．

（1）直接写出点A、点B的坐标：

（2）求AC的长；

（3）点P为平面内一动点，且满足以A、B、C、P为顶点的四边形为平行四边形，请直接回答：

①符合要求的P点有几个？

②写出一个符合要求的P点坐标．

22．（10分）为了从甲、乙两名学生中选拔一人参加射击比赛，对他们的射击水平进行了测验，两人在相同条件下各射靶10次，命中的环数如下：

甲：7、8、6、8、6、5、9、10、7、4

乙：9、5、7、8、7、6、8、6、7、7

如果你是教练你会选拔谁参加比赛？为什么？

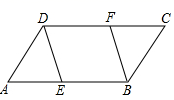
23．（10分）已知两个共一个顶点的等腰Rt△ABC，Rt△CEF，∠ABC=∠CEF=90°，连接AF，M是AF的中点，连接MB、ME．

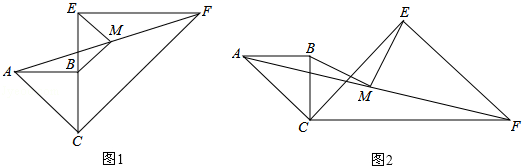
（1）如图1，当CB与CE在同一直线上时，求证：MB∥CF；

（2）如图1，若CB=a，CE=2a，求BM，ME的长；

（3）如图2，当∠BCE=45°时，求证：BM=ME．

24．（12分）在读书月活动中，学校准备购买一批课外读物．为使课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根

据调查结果绘制的两幅不完整的统计图．

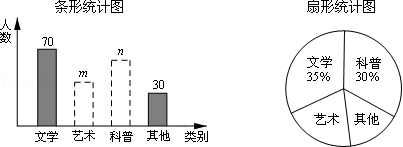
请你根据统计图提供的信息，解答下列问题：

（1）本次调查中，一共调查了　 　名同学；

（2）条形统计图中，m=　 　，n=　 　；

（3）扇形统计图中，艺术类读物所在扇形的圆心角是　 　度；

（4）学校计划购买课外读物6000册，请根据样本数据，估计学校购买其他类读物多少册比较合理？

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、A

4、D

5、C

6、B

7、C

8、A

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、y=1x+1．

12、1．

13、       ；

14、－2

15、5.25×1

16、x(x－9)

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）见解析

18、a-b,-1

19、 (1)见解析；（2）见解析

20、（1）  （2），，，

21、（1）B（0，6），A（﹣8，0）．（2）1；（3）①3个；②P1（﹣1，6），P2（﹣11，﹣6），P3（1，6）．

22、乙同学的成绩较稳定，应选乙参加比赛

23、（1）证明见解析；（2）BM=ME=；（3）证明见解析.

24、解：（1）1．

（2） 40；2．

（3）3．

（4）学校购买其他类读物900册比较合理．