2022-2023学年湖北麻城思源学校数学七下期末学业水平测试试题含答案

这是一份2022-2023学年湖北麻城思源学校数学七下期末学业水平测试试题含答案，共7页。
2022-2023学年湖北麻城思源学校数学七下期末学业水平测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1．化简(-1)2-(-3)0+得(　　)A．0 B．-2 C．1 D．22．某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：时间（小时）
 5
 6
 7
 8
 人数
 10
 15
 20
 5
 则这50名学生这一周在校的平均体育锻炼时间是（   ）A．6.2小时 B．6.4小时 C．6.5小时 D．7小时3．若代数式有意义，则x的取值范围是（　　）A．x≥1 B．x≥0 C．x＞1 D．x＞04．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是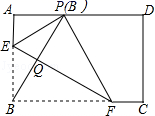（ ）A．①② B．②③ C．①③ D．①④5．如图，图中的小正方形的边长为1，到点A的距离为的格点的个数是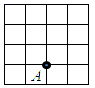（    ）A．7 B．6 C．5 D．46．如图，将△ABC沿着水平方向向右平移后得到△DEF，若BC=3，CE=2，则平移的距离为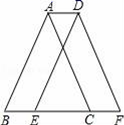（　　）A．1 B．2 C．3 D．47．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，则点P到BC的距离是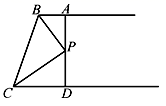（　　）A．8 B．6 C．4 D．28．甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元，若将甲种8千克，乙种10千克，丙种3千克混在一起销售，若要想销售收入保持不变，则售价大概应定为每千克（  ）A．7元 B．6.8元 C．7.5元 D．8.6元9．下列图形中既是轴对称图形又是中心对称图形的是（    ）A．等腰三角形 B．平行四边形 C．正五边形 D．正十边形10．八年级甲、乙、丙三个班的学生人数相同，上期期末体育成绩的平均分相同，三个班上期期末体育成绩的方差分别是：，，，教体育的杜老师更喜欢上体育水平接近的学生，若从这三个班选一个班上课，杜老师更喜欢上课的班是（    ）A．甲班 B．乙班 C．丙班 D．上哪个班都一样二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，∠MON =∠ACB = 90°，AC = BC，AB =5，△ABC顶点A、C分别在ON、OM上，点D是AB边上的中点，当点A在边ON上运动时，点C随之在边OM上运动，则OD的最大值为_____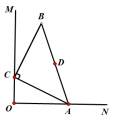．12．写出一个你熟悉的既是轴对称又是中心对称的图形名称______．13．如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，则不等式的解集为________.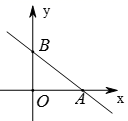14．已知正比例函数y=(k+5)x，且y随x的增大而减小，则k的取值范围是____.15．正比例函数y=kx(k≠0)的图象经过点A(-1,5),则k=__________16．如图所示：分别以直角三角形三边为边向外作三个正方形，其面积分别用、、表示，若，，则的长为__________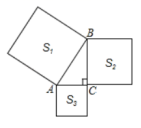．三、解下列各题(本大题共8小题，共72分)17．（8分） “2018年某明星演唱会”于6月3日在某市奥体中心举办．小明去离家300的奥体中心看演唱会，到奥体中心后，发现演唱会门票忘带了，此时离演唱会开始还有30分钟，于是他跑步回家，拿到票后立刻找到一辆“共享单车”原路赶回奥体中心，已知小明骑车的时间比跑步的时间少用了5分钟，且骑车的平均速度是跑步的平均速度的1.5倍．（1）求小明跑步的平均速度；（2）如果小明在家取票和寻找“共享单车”共用了4分钟，他能否在演唱会开始前赶到奥体中心？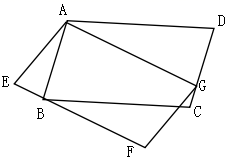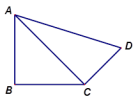说明理由．   18．（8分）如图，平行四边形AEFG的顶点G在平行四边形ABCD的边CD上，平行四边形ABCD的顶点B在平行四边形AEFG的边EF上.求证：□ABCD=□AEFG   19．（8分）如图，在四边形ABCD中，AB=BC=3，CD=，DA=5，∠B=90°，求∠BCD的度数   20．（8分）甲、乙两车间同时从A地出发前往B地，沿着相同的路线匀速驶向B地，甲车中途由于某种原因休息了1小时，然后按原速继续前往B地，两车离A地的距离y(km)与行驶的时间x(h)之间的函数关系如图所示：(1)A、B两地的距离是__________km；(2)求甲车休息后离A地的距离y(km)与x(h)之间的函数关系；(3)请直接写出甲、乙两车何时相聚15km。 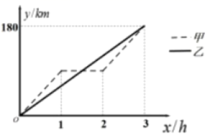  21．（8分）我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.（发现与证明）中，，将沿翻折至，连结.结论1：与重叠部分的图形是等腰三角形；结论2：.试证明以上结论.（应用与探究）在中，已知，，将沿翻折至，连结.若以、、、为顶点的四边形是正方形，求的长.（要求画出图形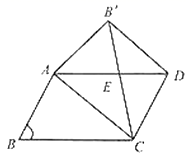）   22．（10分）已知关于的一元二次方程（1）若该方程有两个实数根，求的取值范围；（2）若方程的两个实数根为，且，求的值.   23．（10分）已知直线与轴，轴分别交于点，将对折，使点的对称点落在直线上，折痕交轴于点．（1）求点的坐标；（2）若已知第四象限内的点，在直线上是否存在点，使得四边形为平行四边形？若存在，求出点的坐标；若不存在，说明理由；（3）设经过点且与轴垂直的直线与直线的交点为为线段上一点，求的取值范围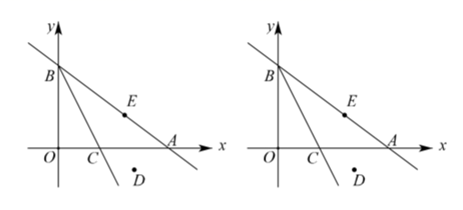．   24．（12分）如图，△ABC中，AB=10，BC=6，AC=8.（1）求证：△ABC是直角三角形；（2）若D是AC的中点，求BD的长.（结果保留根号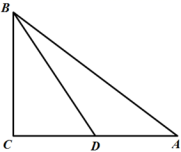）   参考答案 一、选择题(每小题3分,共30分)1、D2、B3、A4、D5、B6、A7、C8、B9、D10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、.12、矩形13、14、k<-515、-1.16、1． 三、解下列各题(本大题共8小题，共72分)17、（1）小明跑步的平均速度为20米/分钟．（2）小明能在演唱会开始前赶到奥体中心．18、证明见解析.19、135°.20、（1）180；（2）；（3）甲乙两车出发0.5h或1.25h或1.75h或2.5h时两车距离15km21、22、（1）；（2）符合条件的的值为23、（1）C（3，0）；（2）不存在；（3）0≤|QA−QO|≤1．24、 (1)见解析;(2)2.