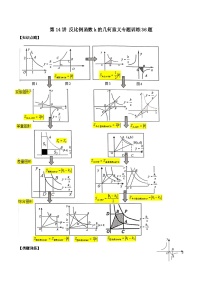
所属成套资源:2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版)
- 第02讲 二次根式的运算专题复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第03讲 一元二次方程单元分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第05讲 平行四边形单元整体分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第06讲 平行四边形存在性问题专题探究-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第07讲 三角形的中位线专题复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
第04讲 一元二次方程几何应用之动点问题专题训练-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版)
展开
这是一份第04讲 一元二次方程几何应用之动点问题专题训练-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版),文件包含第04讲一元二次方程几何应用之动点问题专题训练解析版docx、第04讲一元二次方程几何应用之动点问题专题训练原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
第4讲 一元二次方程几何应用之动点问题专题训练
1.如图,矩形ABCD中,AB=21cm,BC=8cm,动点E从A出发,以3cm/s的速度沿AB向B运动,动点F从C出发,以2cm/s的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是( )
A.3s B.s C.3s或s D.2.5s
【分析】过点E作EM⊥CD于点M,当运动时间为ts时,MF=|21﹣5t|cm,EM=8cm,利用勾股定理,即可得出关于t的一元二次方程,解之即可得出结论.
【解答】解:过点E作EM⊥CD于点M,如图所示.
当运动时间为ts时,AE=3tcm,CF=2tcm,EM=8cm,
∴MF=|AB﹣AE﹣CF|=|21﹣5t|cm.
根据题意得:82+(21﹣5t)2=102,
整理得:5t2﹣42t+81=0,
解得:t1=3,t2=,
∴EF的长为10cm时点E的运动时间是3s或s.
故选:C.
2.如图,在Rt△ABC中,∠B=90°,AB=12cm,AC=13cm,点M从点A出发沿边AB向点B以2cm/s的速度移动,点N从点B出发沿BC边向点C以1cm/s的速度移动.当一个点先到达终点时,另一个点也停止运动,当△MBN的面积为9cm2时,点M,N的运动时间为( )
A.2s B.3s C.4 s D.5s
【分析】在Rt△ABC中,利用勾股定理可求出BC的长度,当运动时间为ts(0≤t≤5)时,BN=tcm,BM=(12﹣2t)cm,根据△MBN的面积为9cm2,即可得出关于t的一元二次方程,解之即可得出结论.
【解答】解:在Rt△ABC中,∠B=90°,AB=12cm,AC=13cm,
∴BC===5(cm).
当运动时间为ts(0≤t≤5)时,AM=2tcm,BN=tcm,BM=(12﹣2t)cm,
依题意得:BN•BM=9,即•t(12﹣2t)=9,
整理得:t2﹣6t+9=0,
解得:t1=t2=3,
∴点M,N的运动时间为3s.
故选:B.
3.如图,在Rt△ABC中,∠B=90°,BC=3cm,AC=5cm,动点P,Q分别从点A,B同时开始运动(运动方向如图所示),点P的速度为cm/s,点Q的速度为1cm/s,点Q运动到点C后停止,点P也随之停止运动,若使△PBQ的面积为cm2,则点P运动的时间是( )
A.2s B.3s C.5s或3s D.5s
【分析】在Rt△ABC中,利用勾股定理可求出AB的长度,当运动时间为ts时,BQ=tcm,BP=(4﹣t)cm,根据△PBQ的面积为cm2,即可得出关于t的一元二次方程,解之取其符合题意的值即可得出结论.
【解答】解:在Rt△ABC中,∠B=90°,BC=3cm,AC=5cm,
∴AB===4(cm).
当运动时间为ts时,AP=tcm,BQ=tcm,BP=(4﹣t)cm,
依题意得:BP•BQ=,
即•(4﹣t)•t=,
整理得:t2﹣8t+15=0,
解得:t1=3,t2=5,
当t=3时,BQ=1×3=3,符合题意;
当t=5时,BQ=1×5=5>3,不符合题意,舍去.
∴点P运动的时间是3s.
故选:B.
4.在△ABC中,∠ABC=90°,AB=6cm,BC=8cm,动点P从点A沿线段AB向点B移动,一动点Q从点B沿线段BC向点C移动,两点同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,当Q到达点C时两点同时停止运动.若使△PBQ的面积为5cm2,则点P运动的时间是( )
A.1s B.4s C.5s或1s D.4s或1s
【分析】设点P运动的时间为ts,则BP=(6﹣t)cm,BQ=2tcm,利用三角形的面积计算公式,即可得出关于t的一元二次方程,解之即可得出t的值,再结合当Q到达点C时两点同时停止运动,即可得出点P运动的时间.
【解答】解:设点P运动的时间为ts,则BP=(6﹣t)cm,BQ=2tcm,
依题意得:(6﹣t)×2t=5,
整理得:t2﹣6t+5=0,
解得:t1=1,t2=5,
∵当Q到达点C时两点同时停止运动,
∴2t≤8,
∴t≤4,
∴t=1.
故选:A.
5.如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=9cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从顶点C出发,沿线段CB向点B方向运动,如果点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,当P,Q两点运动( )秒时,Rt△CPQ的面积等于5cm2.
A.1 B.3 C.3或5 D.1或5
【分析】由题意可得CP=AC﹣2t,CQ=t,则利用三角形的面积公式即可求解.
【解答】解:设运动的时间为ts,
由题意得:CP=AC﹣2t,CQ=t,
∴CP•CQ=(AC﹣2t)t=(12﹣2t)t=﹣t2+6t=5,
解得:t1=1,t2=5,
即当t=1或t=5时,Rt△CPQ的面积等于5cm2.
故选:D.
6.如图,在Rt△ABC中,AC=50m,CB=40m,∠C=90°,点P从点A开始沿AC边向点C以2m/s的速度移动,同时另一个点Q从点C开始沿CB向点B以3m/s的速度移动,当△PCQ的面积等于450m2时,经过的时间是 10s或s .
【分析】利用时间=路程÷速度,可求出点P运动到点C及点Q运动到点B所需时间,设运动时间为xs,当0<x≤时,PC=(50﹣2x)m,CQ=3xm,根据△PCQ的面积等于450m2,即可得出关于x的一元二次方程,解之即可得出x的值;当<x<25时,PC=(50﹣2x)m,CQ=40m,根据△PCQ的面积等于450m2,即可得出关于x的一元一次方程,解之即可得出x的值.综上,此题得解.
【解答】解:50÷2=25(s),40÷3=(秒).
设运动时间为xs.
当0<x≤时,PC=(50﹣2x)m,CQ=3xm,
依题意得:(50﹣2x)•3x=450,
整理得:x2﹣25x+150=0,
解得:x1=10,x2=15(不合题意,舍去);
当<x<25时,PC=(50﹣2x)m,CQ=40m,
依题意得:×40(50﹣2x)=450,
解得:x=.
故答案为:10s或s.
7.如图所示,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点B开始沿BA边以1厘米/秒的速度向A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为24平方厘米?(结果用最简二次根式表示)
【分析】设t秒后△PBQ的面积等于24平方厘米,分别表示出线段PB和线段BQ的长,然后根据△PBQ的面积为24平方厘米列出方程求得时间即可.
【解答】解:设t秒后△PBQ的面积等于24平方厘米,根据题意得:
×2t×t=24,
解得:t1=﹣2(不合题意舍去),t2=2.
答:2秒后△PBQ的面积等于24平方厘米.
8.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t表示移动的时间(0≤t≤6),那么:
(1)求四边形QAPC的面积;
(2)当t为何值时,△PCQ的面积是31cm2?
【分析】(1)当运动时间为ts时,DQ=tcm,AQ=(6﹣t)cm,AP=2tcm,BP=(12﹣2t)cm,利用S四边形QAPC=S矩形ABCD﹣S△CDQ﹣S△BCP,即可求出四边形QAPC的面积;
(2)利用△PCQ的面积=四边形QAPC的面积﹣△APQ的面积,即可得出关于t的一元二次方程,解之即可得出结论.
【解答】解:(1)当运动时间为ts时,DQ=tcm,AQ=(6﹣t)cm,AP=2tcm,BP=(12﹣2t)cm,
∴S四边形QAPC=S矩形ABCD﹣S△CDQ﹣S△BCP
=AB•BC﹣CD•DQ﹣BC•BP
=12×6﹣×12t﹣×6(12﹣2t)
=36(cm2).
答:四边形QAPC的面积为36cm2.
(2)依题意得:36﹣×2t(6﹣t)=31,
整理得:t2﹣6t+5=0,
解得:t1=1,t2=5.
答:当t的值为1或5时,△PCQ的面积是31cm2.
9.如图,在△ABC中,∠B=90°,AB=5cm,BC=8cm.点P从点A开始沿AB边向点B以1cm/s的速度移动、同时点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点时,另外一点也随之停止运动.
(1)△PQB的面积能否等于9cm2?请说明理由.
(2)几秒后,四边形APQC的面积等于16cm2?请写出过程.
【分析】(1)根据△PQB的面积等于9cm2,即可得出关于t的一元二次方程,由根的判别式Δ=﹣11<0,可得所列方程没有实数根,进而得出△PQB的面积不等等于9cm2;
(2)根据四边形APQC的面积等于16cm2,即可得出关于t的一元二次方程,解之即可得出t的值.
【解答】解:(1)△PQB的面积不能等于9cm2,
理由如下:
∵5÷1=5s,8÷2=4s,
∴运动时间t的取值范围为:0≤t≤4,
根据题意可得:AP=tm,BP=(5﹣t)cm,BQ=2tcm,
假设△PQB的面积等于9cm2,
则,
整理得:t2﹣5t+9=0,
∵Δ=(﹣5)2﹣4×1×9=﹣11<0,
∴所列方程没有实数根,
∴△PQB的面积不能等于9cm2;
(2)由(1)得:AP=tcm,BP=(5﹣t)cm,BQ=2tcm,运动时间t的取值范围为:0≤t≤4,
∵四边形APQC的面积等于16cm2,
∴,
整理得:t2﹣5t+4=0,
解得t1=1,t2=4,
∴t=1或4时,四边形APQC的面积等于16cm2.
答:1s或4秒后,四边形APQC的面积等于16cm2.
10.如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从C出发沿着CB边以1cm/s的速度运动,另一动点Q从A出发沿着AC边以2cm/s的速度运动,P,Q两点同时出发,运动时间为t(s).
(1)当t为几秒时,△PCQ的面积是△ABC面积的?
(2)△PCQ的面积能否为△ABC面积的一半?若能,求出t的值;若不能,说明理由.
【分析】(1)根据三角形的面积公式可以求出时间t;
(2)由等量关系S△PCQ=S△ABC列方程求出t的值,但方程无解.
【解答】解:(1)∵S△PCQ=t(8﹣2t),S△ABC=×4×8=16,
∴t(8﹣2t)=16×,
整理得t2﹣4t+4=0,
解得t=2.
答:当t=2s时△PCQ的面积为△ABC面积的;
(2)当S△PCQ=S△ABC时,t(8﹣2t)=16×,
整理得t2﹣4t+8=0,
Δ=(﹣4)2﹣4×1×8=﹣16<0,
∴此方程没有实数根,
∴△PCQ的面积不可能是△ABC面积的一半.
11.如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm.点P、Q同时由A、C两点出发,分别以1cm/s和2cm/s的速度沿线段AC、CB匀速移动,当一点到达终点时,另一点也停止移动.
(1)设经过t秒,用含t的代数式表示PC、CQ,PC= (6﹣t)cm ,CQ= 2tcm ;
(2)几秒后,△PCQ的面积是△ABC面积的?
【分析】(1)根据路程=速度×时间,结合线段的和差关系即可求解;
(2)根据△PCQ的面积是△ABC面积的,列出方程计算即可求解.
【解答】解:(1)PC=(6﹣t)cm,CQ=2tcm.
故答案为:(6﹣t)cm,2tcm;
(2)依题意有:×2t(6﹣t)=×6×8×,
解得t1=2,t2=4.
故2或4秒后,△PCQ的面积是△ABC面积的.
12.如图,等腰直角三角形ABC中,AB=BC=8cm,点P从点A开始沿AB边向点B运动,过点P作PR∥BC,PQ∥AC,分别交AC,BC于R,Q.
(1)四边形PQCR的形状是 平行四边形 ;若设AP=x,则四边形PQCR的面积可表示为 (﹣x2+8x)cm2 .
(2)四边形PQCR的面积能为16cm2吗?能为20cm2吗?如果能,请求出P点与A点之间的距离;如果不能,请说明理由.
【分析】(1)由“PR∥BC,PQ∥AC”,可得出四边形PQCR的形状是平行四边形,设AP=xcm,则PR=xcm,BP=BQ=(8﹣x)cm,利用四边形PQCR的面积=三角形ABC的面积﹣三角形APR的面积﹣三角形PBQ的面积,即可找出四边形PQCR的面积;
(2)四边形PQCR的面积能为16cm2,由(1)的结论结合四边形PQCR的面积为16cm2,即可得出关于x的一元二次方程,解之即可得出结论;四边形PQCR的面积不能为20cm2,由(1)的结论结合四边形PQCR的面积为20cm2,即可得出关于x的一元二次方程,由根的判别式Δ=﹣16<0,可得出该方程无实数根,即四边形PQCR的面积不能为20cm2.
【解答】解:(1)∵PR∥BC,PQ∥AC,
∴四边形PQCR的形状是平行四边形.
设AP=xcm,则PR=xcm,BP=BQ=(8﹣x)cm,
∴四边形PQCR的面积=AB•BC﹣AP•PR﹣BP•BQ
=×8×8﹣•x•x﹣•(8﹣x)•(8﹣x)
=﹣x2+8x.
故答案为:平行四边形;(﹣x2+8x)cm2.
(2)四边形PQCR的面积能为16cm2,
依题意得:﹣x2+8x=16,
整理得:x2﹣8x+16=0,
解得:x1=x2=4,
∴P点与A点之间的距离为4cm时,四边形PQCR的面积为16cm2;
四边形PQCR的面积不能为20cm2,理由如下:
依题意得:﹣x2+8x=20,
整理得:x2﹣8x+20=0,
∵Δ=(﹣8)2﹣4×1×20=﹣16<0,
∴该方程无实数根,
即四边形PQCR的面积不能为20cm2.
13.如图,四边形ABCD两条对角线AC、BD互相垂直,且AC+BD=10.
设AC=x,(0<x<5)
(1)用含x的式子表示:S四边形ABCD= ﹣x2+5x ;
(2)当四边形ABCD四边形的面积为8cm2时,求AC、BD的长.
【分析】(1)设AC,BD交于O,根据三角形的面积公式即可得到结论;
(2)根据题意得到方程,解方程即可得到结论.
【解答】解:(1)设AC,BD交于O,
∵AC+BD=10,AC=x,
∴BD=10﹣x,
∵AC⊥BD,
∴S四边形ABCD=S△ABC+S△ADC=AC•DO+AC•BO=AC•BD=x(10﹣x)=﹣x2+5x;
故答案为:﹣x2+5x;
(2)∵四边形ABCD四边形的面积为8cm2,
∴﹣x2+5x=8,
解得x1=2,x2=8(不合题意舍去),
∴AC=2cm,BD=8cm.
14.如图,在△ABC中,∠A=90°,AB=12cm,AC=8cm,现有动点P从点B出发,沿射线BA方向运动,动点Q从点C出发,沿射线CA方向运动,已知点P的速度是2cm/s,点Q的速度是1cm/s.它们同时出发,设运动时间是ts(t>0).
(1)当t=4时,求△APQ的面积.
(2)经过多少秒时,△APQ的面积是△ABC面积的一半.
【分析】(1)根据各边之间的关系,可找出当t=4时AP,AQ的长,再利用三角形的面积计算公式,即可求出结论;
(2)利用时间=路程÷速度,可分别求出点P,Q到达点A的时间,分0<t<6,6<t<8及t>8三种情况考虑,根据△APQ的面积是△ABC面积的一半,即可得出关于t的一元二次方程,解之取其符合题意的值即可得出结论.
【解答】解:(1)当t=4时,BP=2×4=8(cm),CQ=1×4=4(cm),
∴AQ=AC﹣CQ=8﹣4=4(cm),AP=AB﹣BP=12﹣8=4(cm),
∴△APQ的面积=AQ•AP=×4×4=8(cm2).
答:当t=4时,△APQ的面积为8cm2.
(2)12÷2=6(秒),8÷1=8(秒).
当0<t<6时,AP=(12﹣2t)cm,AQ=(8﹣t)cm,
∴(12﹣2t)(8﹣t)=××12×8,
整理得:t2﹣14t+24=0,
解得:t1=2,t2=12(不符合题意,舍去);
当6<t<8时,AP=(2t﹣12)cm,AQ=(8﹣t)cm,
∴(2t﹣12)(8﹣t)=××12×8,
整理得:t2﹣14t+72=0,
∵Δ=(﹣14)﹣4×1×72=﹣92<0,
∴方程无解;
当t>8时,AP=(2t﹣12)cm,AQ=(t﹣8)cm,
∴(2t﹣12)(t﹣8)=××12×8,
整理得:t2﹣14t+24=0,
解得:t1=2(不符合题意,舍去),t2=12.
综上所述,经过2秒或12秒时,△APQ的面积是△ABC面积的一半.
15.等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)当点P在边AB上运动时,作PE⊥AC于点E,请问:线段DE的长度是否改变?如果不改变,请求出这个定值,如果改变,请说明理由.
【分析】(1)分两种情况推理即可;
(1)根据三角形的面积公式解答即可;
(3)由等腰直角三角形和平行四边形进行解答即可.
【解答】解:(1)当t<10秒时,P在线段AB上,此时CQ=t,PB=10﹣t,
∴S=×t(10﹣t)=(10t﹣t2),
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t﹣10,
∴S=×t(t﹣10)=(t2﹣10t).
(2)∵S△ABC=,
∴当t<10秒时,S△PCQ=,
整理得t2﹣10t+100=0,此方程无解,
当t>10秒时,S△PCQ=,
整理得t2﹣10t﹣100=0,解得t=5±5(舍去负值),
∴当点P运动5+5秒时,S△PCQ=S△ABC.
(3)当点P、Q运动时,线段DE的长度不会改变,
证明:过Q作QM⊥AC,交直线AC于点M,
∵△ABC是等腰直角三角形,
∴∠A=∠ACB=∠QCM=45°,
∴△APE和△QCM都是等腰直角三角形,
∵AP=CQ,
∴AE=PE=CM=QM=t,
∴四边形PEQM是平行四边形,且DE是对角线EM的一半.
又∵EM=AC=10,
∴DE=5,
∴当点P、Q运动时,线段DE的长度不会改变.
16.如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动至A.设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②是否存在t的值,使△APQ面积为△APC的一半?若存在,请求出t的值;若不存在,请说明理由.
③是否存在t的值,使△APQ为以AQ为底的等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
【分析】(1)把P(m,3)的坐标代入直线l1上的解析式即可求得P的坐标,然后根据待定系数法即可求得b;
(2)根据直线l2的解析式得出C的坐标,
①根据题意得出AQ=9﹣t,然后根据S=AQ•|yP|即可求得△APQ的面积S与t的函数关系式;
②结合①的结论列方程可得答案;
③当PQ=AQ时,可得(t﹣7+1)2+(0﹣3)2=(t﹣7﹣2)2,即可解得答案.
【解答】解;(1)∵点P(m,3)为直线l1上一点,
∴3=﹣m+2,解得m=﹣1,
∴点P的坐标为(﹣1,3),
把点P的坐标代入y2=x+b得,3=×(﹣1)+b,
解得b=;
(2)∵b=,
∴直线l2的解析式为y=x+,
令y=0得x=﹣7,
∴C点的坐标为(﹣7,0),
①由直线l1:y1=﹣x+2可知A(2,0),
∴AQ=2+7﹣t=9﹣t,
∴S=AQ•|yP|=×(9﹣t)×3=﹣t;
②存在t的值,使△APQ面积为△APC的一半,理由如下:
根据题意得:﹣t=×9×3×,
解得t=,
∴t的值为时,使△APQ面积为△APC的一半;
③存在t的值,使△APQ为以AQ为底的等腰三角形,理由如下:
∵CQ=t,C(﹣7,0),
∴Q(﹣7+t,0),
∵A(2,0),P(﹣1,3),
∴(t﹣7+1)2+(0﹣3)2=(2+1)2+(0﹣3)2,
∴(t﹣6)2=32,
解得t=3或t=9(舍去),
当t的值为3时,△APQ为以AQ为底的等腰三角形.
相关试卷
这是一份【重难点讲义】浙教版数学八年级下册-第04讲 一元二次方程几何应用之动点问题专题训练,文件包含重难点讲义浙教版数学八年级下册-第04讲一元二次方程几何应用之动点问题专题训练原卷版docx、重难点讲义浙教版数学八年级下册-第04讲一元二次方程几何应用之动点问题专题训练解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
这是一份【重难点讲义】浙教版数学七年级上册-第04讲 数轴动点问题专题探究,文件包含第04讲数轴动点问题专题探究原卷版docx、第04讲数轴动点问题专题探究解析版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
这是一份第15讲 反比例函数与几何图形的综合-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版),文件包含第15讲反比例函数与几何图形的综合原卷版docx、第15讲反比例函数与几何图形的综合解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。