第06讲 平行四边形存在性问题专题探究-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版)

第6讲  平行四边形存在性问题专题探究

【知识点睛】

        知识储备：①平行四边形是中心对称图形

          ②中心对称图形的性质：对称中心平分中心对称图形内通过该点的任意线段，且使中心对称图形的面积被平分

          ③中点公式：

        方法策略：

（1）有3个定点，找第4个点形成平行四边形时：

①设第4个点的坐标

②以3个定点组成的3条线段为对角线分类讨论

③以中心对称图形的性质为等量关系列式求解

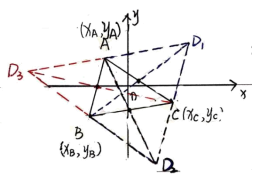
例，如图所示，平面直角坐标系内有A、B、C三点，在平面内找第4个点，构成平行四边形；

（2）有2个定点，且另外两个动点均在特殊的位置上时，方法策略同上。

类型一  几何背景下的平行四边形存在性问题

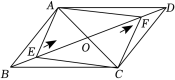
1．如图，平行四边形ABCD的对角线AC，BD相交于点O，BD＝12cm，AC＝6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动．若点E，F同时运动，设运动时间为t秒，当t＝　   　时，四边形AECF是平行四边形．

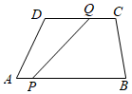
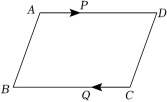
2．如图，四边形ABCD中，AB∥DC，DC＝6cm，AB＝9cm．点P以1cm/s的速度由A点向B点运动，同时点Q以2cm/s的速度由C点向D点运动，其中一点到达终点时，另一点也停止运动，当线段PQ将四边形ABCD截出一个平行四边形时，此时的运动时间为  

 　   　s．

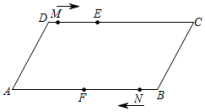
3．如图，在▱ABCD中，AB＝10cm，F是AB的中点，E为边CD上一点，DE＝4cm．点M从D点出发，沿D→C以1cm/s的速度匀速运动到点C；同时点N从点B出发，沿B→A以2cm/s的速度匀速运动到点A．一个点停止运动后，另一个点也随之停止运动．当点M运动时间是 　   　秒时，以点M，E，N，F为顶点的四边形是平行四边形．

4．如图，在▱ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∠FBM＝∠CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动；点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动，点P运动到F点时停止运动，点O也同时停止运动，当点P运动（　　）秒时，以点P、Q、E、F为顶点的四边形是平行四边形．

A．3 B．3或5 C．5 D．4或5

5．如图所示，在平行四边形ABCD中，AB＝5cm，AD＝9cm．点P在AD边上以1cm/s的速度从点A向点D运动，点Q在BC边上以4cm/s的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时，P、Q同时停止运动，设运动时间为t（s）且t＞0，当以P，D，Q，B为顶点的四边形是平行四边形时，则t的所有可能值为 　   　．

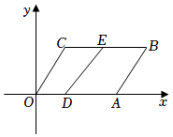
6．如图，在平面直角坐标系中，已知点A的坐标为（9，0），点C的坐标为（3，3），四边形OABC是平行四边形，点D、E份别在边OA、BC上，且OD＝OA，CE＝4．动点P、Q在平行四边形OABC的一组邻边上，以点D、E、P、Q为顶点的四边形是平行四边形时，其面积为 　   　．

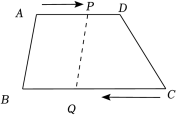
7．如图，在四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，动点P、Q分别从A、C同时出发，点P以1cm/s的速度由A向D运动，点Q以3cm/s的速度由C向B运动，其中一动点到达终点时，另一动点随之停止运动，设运动时间为t秒．

（1）AP＝　   　，BQ＝　   　，（分别用含有t的式子表示）；

（2）当四边形PQCD的面积是四边形ABQP面积的2倍时，求出t的值．

（3）当点P、Q与四边形ABCD的任意两个顶点所形成的四边形是平行四边形时，直接写出t的值．

类型二  “三定一动”求平行四边形的顶点坐标

1．在平面直角坐标系xOy中，已知A（1，﹣1），B（4，2），C（0，3），下列坐标不能与A、B、C构成平行四边形的是（　　）

A．（﹣3，0） B．（5，﹣2） C．（3，6） D．（﹣3，﹣2）

2．在平面直角坐标系中，点A、B、C的坐标分别是A（﹣2，5），B（﹣3，﹣1），C（1，﹣1），在x轴上方找到点D，使以A，B，C，D为顶点的四边形是平行四边形，那么点D的坐标是　   　．

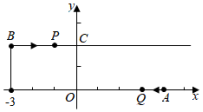
3．在平面直角坐标系中，已知点A（4，0），点B（﹣3，2），点C（0，2），点P从点B出发，以2个单位每秒的速度沿射线BC运动，点Q从点A出发，开始以1个单位每秒的速度向原点O运动，到达原点后立刻以原来3倍的速度沿射线OA运动，若P，Q两点同时出发，设运动时间为t秒，则当t＝　   　时，以点A，Q，C，P为顶点的四边形为平行四边形．

4．如图，在平面直角坐标系的第一象限找一点A，第二象限找一点B，使OA＝，OB＝2，AB＝5，且A，B都是格点，连接OA，OB，AB．（画出一个△OAB即可）．

（1）判断△OAB的形状，并说明理由；

（2）是否存在点C，使得O，A，B，C四点构成的四边形为平行四边形？如果存在，请直接写出点C的坐标；如果不存在，请说明理由．

5．如图，在平面直角坐标系中，矩形OABC的三个顶点A，O，C在坐标轴上，矩形的面积为12，对角线AC所在直线的解析式为y＝kx﹣4k（k≠0）．

（1）求A，C的坐标；

（2）若D为AC中点，过D的直线交y轴负半轴于E，交BC于F，且OE＝1，求直线EF的解析式；

（3）在（2）的条件下，在坐标平面内是否存在一点G，使以C，D，F，G为顶点的四边形为平行四边形？若存在，请直接写出点G的坐标；若不存在，请说明理由．

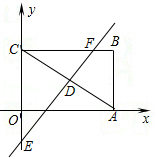
类型三  “两定两动”求平行四边形的顶点坐标

1．在平面直角坐标系中，已知A（﹣4，2），B（2，5），在x轴、y轴上分别有两动点C、D，若以点A，B，C，D为顶点的四边形是平行四边形，则点C的坐标为　   　．

2．在平面直角坐标系中，A（﹣1，1），B（3，2），C（2m，3m+1），点D在直线y＝﹣1上，若以A，B，C，D四点为顶点的四边形是平行四边形，则点D的坐标为 　   　．

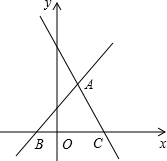
3．如图，在平面直角坐标系xOy，直线y＝x+1与y＝﹣2x+4交于点A，两直线与x轴分别交于点B和点C，D是直线AC上的一个动点，直线AB上是否存在点E，使得以E，D，O，A为顶点的四边形是平行四边形？若存在，求出点E的坐标；若不存在，请说明理由．

4．如图，在平面直角坐标系中，直线y＝﹣x+3与x轴、y轴相交于A、B两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到线段CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．

（1）求证：△BOC≌△CED；

（2）请直接写出点D的坐标，并求出直线BC的函数关系式；

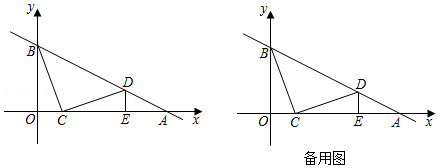（3）若点P是x轴上的一个动点，点Q是线段CB上的点（不与点B、C重合），是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的P点坐标．若不存在，请说明理由．

5．如图，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在x轴上，点C在y轴上，OA＝6，∠CAO＝30°，将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．

（1）求点D的坐标；

（2）在线段AC上有一动点P，连接EP和OP，求当△OPE周长最小时，点P的坐标，若M，N是x轴上两动点（M在点N左侧）且MN＝1，求当四边形CMNP周长最小时，M点的坐标；

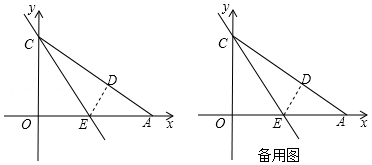（3）设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．