


2022-2023学年湖南省长沙市师大附中教育集团第十七下数学期末联考模拟试题含答案
展开
这是一份2022-2023学年湖南省长沙市师大附中教育集团第十七下数学期末联考模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列说法正确的是等内容,欢迎下载使用。
2022-2023学年湖南省长沙市师大附中教育集团第十七下数学期末联考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知一个多边形内角和是外角和的4倍,则这个多边形是( )A.八边形 B.九边形 C.十边形 D.十二边形2.下列描述一次函数y=﹣2x+5的图象和性质错误的是( )A.y随x的增大而减小 B.直线与x轴交点的坐标是(0,5)C.当x>0时y<5 D.直线经过第一、二、四象限3.某跳远队准备从甲、乙、丙、丁4名运动员中选取成绩好且稳定的一名选手参赛,经测试,他们的成绩如下表,综合分析应选( )成绩甲乙丙丁平均分(单位:米)6.06.15.54.6方差0.80.20.30.1A.甲 B.乙 C.丙 D.丁4.如图,一次函数y=kx+b的图象与y轴交于点(0,1),则关于x的不等式kx+b>1的解集是( )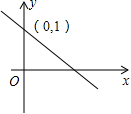 A.x>0 B.x<0 C.x>1 D.x<15.欧几里得是古希腊数学家,所著的《几何原本》闻名于世.在《几何原本》中,形如x2+ax=b2的方程的图解法是:如图,以
A.x>0 B.x<0 C.x>1 D.x<15.欧几里得是古希腊数学家,所著的《几何原本》闻名于世.在《几何原本》中,形如x2+ax=b2的方程的图解法是:如图,以![]() 和b为直角边作Rt△ABC,再在斜边上截取BD=
和b为直角边作Rt△ABC,再在斜边上截取BD=![]() ,则图中哪条线段的长是方程x2+ax=b2的解?答:是( )
,则图中哪条线段的长是方程x2+ax=b2的解?答:是( ) 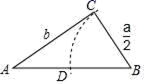 A.AC B.AD C.AB D.BC6.如图,已知一次函数
A.AC B.AD C.AB D.BC6.如图,已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,则根据图象可得不等式
,则根据图象可得不等式![]() 的解集是( )
的解集是( )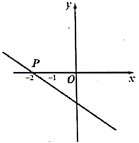 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,已知
7.如图,已知![]() 的顶点A和AB边的中点C都在双曲线
的顶点A和AB边的中点C都在双曲线![]() 的一个分支上,点B在x轴上,则
的一个分支上,点B在x轴上,则![]() 的面积为
的面积为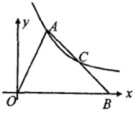 A.3 B.4 C.6 D.88.将直线y=-2x-3怎样平移可以得到直线y=-2x的是( )A.向上平移2个单位 B.向上平移3个单位C.向下平移2个单位 D.向下平移3个单位9.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为1
A.3 B.4 C.6 D.88.将直线y=-2x-3怎样平移可以得到直线y=-2x的是( )A.向上平移2个单位 B.向上平移3个单位C.向下平移2个单位 D.向下平移3个单位9.如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为1![]() ﹣6;④当OD⊥AD时,BP=1.其中结论正确的有( )
﹣6;④当OD⊥AD时,BP=1.其中结论正确的有( )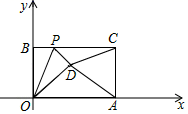 A.1个 B.1个 C.3个 D.4个10.下列说法正确的是( )A.某个对象出现的次数称为频率 B.要了解某品牌运动鞋使用寿命可用普查C.没有水分种子发芽是随机事件 D.折线统计图用于表示数据变化的特征和趋势11.小华同学某体育项目7次测试成绩如下(单位:分):9,7,1,8,1,9,1.这组数据的中位数和众数分别为( )A.8,1 B.1,9 C.8,9 D.9,112.如果多项式
A.1个 B.1个 C.3个 D.4个10.下列说法正确的是( )A.某个对象出现的次数称为频率 B.要了解某品牌运动鞋使用寿命可用普查C.没有水分种子发芽是随机事件 D.折线统计图用于表示数据变化的特征和趋势11.小华同学某体育项目7次测试成绩如下(单位:分):9,7,1,8,1,9,1.这组数据的中位数和众数分别为( )A.8,1 B.1,9 C.8,9 D.9,112.如果多项式![]() 是一个完全平方式,那么
是一个完全平方式,那么![]() 的值为
的值为![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=_______.14.从甲、乙两班分别任抽30名学生进行英语口语测验,两个班测试成绩的方差是
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=_______.14.从甲、乙两班分别任抽30名学生进行英语口语测验,两个班测试成绩的方差是![]() ,
,![]() ,则_________班学生的成绩比较整齐.15.直线l与直线y=3﹣2x平行,且在y轴上的截距是﹣5,那么直线l的表达式是_____.16.将抛物线
,则_________班学生的成绩比较整齐.15.直线l与直线y=3﹣2x平行,且在y轴上的截距是﹣5,那么直线l的表达式是_____.16.将抛物线![]() 先向左平移
先向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得抛物线的解析式为______.17.如图显示了小亚用计算机模拟随机投掷一枚某品牌啤酒瓶盖的实验结果.
个单位,所得抛物线的解析式为______.17.如图显示了小亚用计算机模拟随机投掷一枚某品牌啤酒瓶盖的实验结果.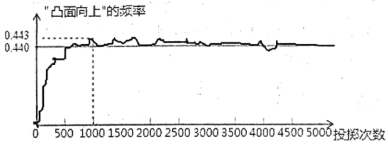 那么可以推断出如果小亚实际投掷一枚品牌啤酒瓶盖时,“凸面向上”的可能性 _________“凹面向上”的可能性.(填“大于”,“等于”或“小于”).三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在
那么可以推断出如果小亚实际投掷一枚品牌啤酒瓶盖时,“凸面向上”的可能性 _________“凹面向上”的可能性.(填“大于”,“等于”或“小于”).三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在![]() 中,
中,![]() ,
,![]() 是中线,
是中线,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.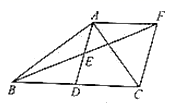 19.(5分)在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:摸到球的次数
19.(5分)在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:摸到球的次数![]() 10020030050080010003000摸到白球的次数
10020030050080010003000摸到白球的次数![]() 651241783024815991803摸到白球的概率
651241783024815991803摸到白球的概率![]() 0.650.620.5930.6040.6010.5990.601(1)请估计当
0.650.620.5930.6040.6010.5990.601(1)请估计当![]() 很大时,摸到白球的频率将会接近______;(精确到0.1);(2)假如随机摸一次,摸到白球的概率P(白球)=______;(3)试估算盒子里白色的球有多少个? 20.(8分)已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.(1)求证:四边形FBGH是菱形;(2)求证:四边形ABCH是正方形.
很大时,摸到白球的频率将会接近______;(精确到0.1);(2)假如随机摸一次,摸到白球的概率P(白球)=______;(3)试估算盒子里白色的球有多少个? 20.(8分)已知:如图,在△ABC中,AB=BC,∠ABC=90°,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H,连接HA、HC.(1)求证:四边形FBGH是菱形;(2)求证:四边形ABCH是正方形.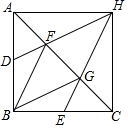 21.(10分)先化简,再求值:
21.(10分)先化简,再求值:![]() ÷(x﹣
÷(x﹣![]() ),其中x=
),其中x=![]() +1. 22.(10分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):方案A:每千克5.8元,由基地免费送货;方案B:每千克5元,客户需支付运费2 000元.(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;(2)求购买量x在什么范围时,选用方案A比方案B付款少;(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案. 23.(12分)如图,在平面直角坐标系中,直线l:y=﹣
+1. 22.(10分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):方案A:每千克5.8元,由基地免费送货;方案B:每千克5元,客户需支付运费2 000元.(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;(2)求购买量x在什么范围时,选用方案A比方案B付款少;(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案. 23.(12分)如图,在平面直角坐标系中,直线l:y=﹣![]() x+2与x轴交于点B,与y轴交于点A,以AB为斜边作等腰直角△ABC,使点C落在第一象限,过点C作CD⊥AB于点D,作CE⊥x轴于点E,连接ED并延长交y轴于点F.(1)如图(1),点P为线段EF上一点,点Q为x轴上一点,求AP+PQ的最小值.(2)将直线l进行平移,记平移后的直线为l1,若直线l1与直线AC相交于点M,与y轴相交于点N,是否存在这样的点M、点N,使得△CMN为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
x+2与x轴交于点B,与y轴交于点A,以AB为斜边作等腰直角△ABC,使点C落在第一象限,过点C作CD⊥AB于点D,作CE⊥x轴于点E,连接ED并延长交y轴于点F.(1)如图(1),点P为线段EF上一点,点Q为x轴上一点,求AP+PQ的最小值.(2)将直线l进行平移,记平移后的直线为l1,若直线l1与直线AC相交于点M,与y轴相交于点N,是否存在这样的点M、点N,使得△CMN为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.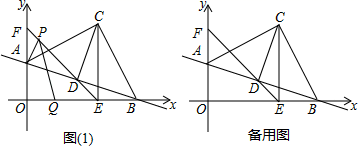 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、B3、B4、B5、B6、D7、C8、B9、D10、D11、D12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、B3、B4、B5、B6、D7、C8、B9、D10、D11、D12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 或
或![]() 14、乙15、y=﹣2x﹣116、
14、乙15、y=﹣2x﹣116、![]() 17、小于 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、见解析.19、(1)0.1;(2)0.1;(3)30个20、(1)见解析 (2)见解析21、
17、小于 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、见解析.19、(1)0.1;(2)0.1;(3)30个20、(1)见解析 (2)见解析21、![]() .22、 (1)方案A:y=5.8x;方案B:y=5x+2 000(2)选用方案A比方案B付款少(3) B23、(1)AP+PQ的最小值为1;(2)存在,M点坐标为(﹣12,﹣1)或(12,8).
.22、 (1)方案A:y=5.8x;方案B:y=5x+2 000(2)选用方案A比方案B付款少(3) B23、(1)AP+PQ的最小值为1;(2)存在,M点坐标为(﹣12,﹣1)或(12,8).
相关试卷
这是一份2023-2024学年湖南省长沙市师大附中教育集团八上数学期末联考试题含答案,共7页。试卷主要包含了下列实数中,是无理数的是,若分式等于零,则的值是,对不等式进行变形,结果正确的是等内容,欢迎下载使用。
这是一份湖南省长沙市雅礼教育集团2022-2023学年数学七下期末检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,若函数有意义,则等内容,欢迎下载使用。
这是一份湖南省长沙市师大附中教育集团2022-2023学年数学七下期末检测模拟试题含答案,共6页。试卷主要包含了某校40名学生参加科普知识竞赛,下列四个选项中,错误的是等内容,欢迎下载使用。









