


2022-2023学年甘肃省定西市名校数学七下期末达标测试试题含答案
展开2022-2023学年甘肃省定西市名校数学七下期末达标测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,则根据图象可得不等式
,则根据图象可得不等式![]() 的解集是( )
的解集是( )
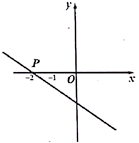
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列图形中,是轴对称图形的是( )
A. B.
B. C.
C.![]() D.
D.![]()
3.下列条件,不能判断四边形![]() 是平行四边形的是( )
是平行四边形的是( )
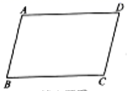
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
4.若分式![]() 的值为0,则( )
的值为0,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,在![]() 中,
中,![]() ,AD平分
,AD平分![]() ,
,![]() ,
,![]() ,那么点D到直线AB的距离是( )
,那么点D到直线AB的距离是( )
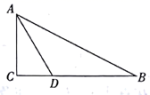
A.2cm B.4cm C.6cm D.10cm
6.若一次函数y=x+4的图象上有两点A(﹣![]() ,y1)、B(1,y2),则下列说法正确的是( )
,y1)、B(1,y2),则下列说法正确的是( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
7.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=7
8.在函数![]() 的图象上的点是( )
的图象上的点是( )
A.(-2,12) B.(2,- 12) C.(-4,- 6) D.(4,- 6)
9.若分式![]() 有意义,则x的取值范围是
有意义,则x的取值范围是
A.x>1 B.x<1 C.x≠1 D.x≠0
10.下列根式中,属于最简二次根式的是( )
A.-![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在平面直角坐标系中,已知一次函数y=![]() x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”).
x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”).
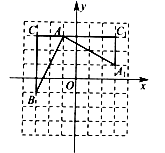
12.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为______.
13.如图,在平面直角坐标系中,已知![]() 顶点的坐标分别为
顶点的坐标分别为![]() ,且
,且![]() 是由
是由![]() 旋转得到.若点
旋转得到.若点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 轴上,要使四边形
轴上,要使四边形![]() 为平行四边形,则满足条件的点
为平行四边形,则满足条件的点![]() 的坐标为______.
的坐标为______.
14.分解因式:![]() ___.
___.
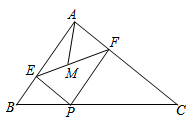
15.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,P为BC上一动点,
,P为BC上一动点,![]() 于E,
于E,![]() 于F,M为EF的中点,则AM的最小为___.
于F,M为EF的中点,则AM的最小为___.
16.学校篮球集训队11名队员进行定点投篮训练,将11名队员在1分钟内投进篮筐的球数由小到大排序后为6,7,8,9,9,9,9,10,10,10,12,这组数据的众数和中位数分别是______________.
三、解下列各题(本大题共8小题,共72分)
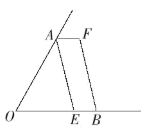
17.(8分)如图,已知∠AOB,OA=OB,点E在边OB上,四边形AEBF是平行四边形.
(1)请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不写作法)
(2)请说明你的画法的正确性.
18.(8分)瑞安市文化创意实践学校是一所负责全市中小学生素质教育综合实践活动的公益类事业单位,学校目前可开出:创意手工创意表演、科技制作(创客)、文化传承、户外拓展等5个类别20多个项目课程.
(1)学校3月份接待学生1000人,5月份增长到2560人,求该学校接待学生人数的平均月增长率是多少?
(2)在参加“创意手工”体验课程后,小明发动本校同学将制作的作品义卖募捐.当作品卖出的单价是2元时,每天义卖的数量是150件;当作品的单价每涨高1元时,每天义卖的数量将减少10件.问:在作品单价尽可能便宜的前提下,当单价定为多少元时,义卖所得的金额为600元?
19.(8分)某产品成本为400元/件,由经验得知销售量![]() 与售价
与售价![]() 是成一次函数关系,当售价为800元/件时能卖1000件,当售价1000元/件时能卖600件,问售价多少时利润
是成一次函数关系,当售价为800元/件时能卖1000件,当售价1000元/件时能卖600件,问售价多少时利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
20.(8分)如图,在□ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H,求证:AG=CH.
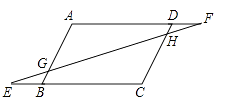
21.(8分)已知:如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,设
的中点,设![]() ,
,![]() .
.
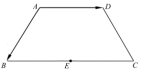
(1)填空:![]() ________;
________;![]() ________;
________;![]() ________;(用
________;(用![]() ,
,![]() 的式子表示)
的式子表示)
(2)在图中求作![]() .(不要求写出作法,只需写出结论即可)
.(不要求写出作法,只需写出结论即可)
22.(10分)已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2,连接CE,在不添加任何辅助线的情况下,请直接写出图2中所有与△BDE面积相等的三角形.
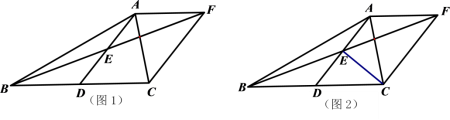
23.(10分)问题发现:
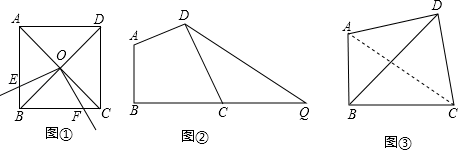
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
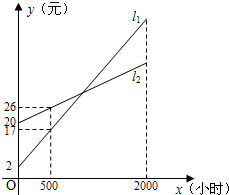
24.(12分)如图所示,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (元,分别用y1与y2表示)与照明时间
(元,分别用y1与y2表示)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(1)根据图象分别求出![]() ,
,![]() 对应的函数(分别用y1与y2表示)关系式;
对应的函数(分别用y1与y2表示)关系式;
(2)对于白炽灯与节能灯,请问该选择哪一种灯,使用费用会更省?
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、D
4、B
5、B
6、C
7、D
8、C
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、 (−1.5,2)或(−3.5,−2)或(−0.5,4).
14、![]()
15、2.1.
16、9;9
三、解下列各题(本大题共8小题,共72分)
17、(1)射线OP即为所求,见解析;(2)见解析.
18、(1)该学校接待学生人数的增长率为60%;(2)单价定为5元.
19、售价为850元/件时,有最大利润405000元
20、证明见解析.
21、(1)![]() ;
;![]() ;
;![]() (或
(或![]() );(2)图见解析,
);(2)图见解析,![]() .
.
22、 (1)证明见解析;(2)△AEF、 △ABE、 △ACE 、△CDE.
23、(1)4;(2)5![]() ;(3)600(
;(3)600(![]() +1).
+1).
24、(1)y1=![]() x+2,y2=
x+2,y2=![]() x+20(2)见解析
x+20(2)见解析
西藏拉萨市名校2022-2023学年数学七下期末达标检测试题含答案: 这是一份西藏拉萨市名校2022-2023学年数学七下期末达标检测试题含答案,共8页。试卷主要包含了若,则代数式的值是,如图等内容,欢迎下载使用。
甘肃省定西市渭源县2022-2023学年数学七下期末联考模拟试题含答案: 这是一份甘肃省定西市渭源县2022-2023学年数学七下期末联考模拟试题含答案,共5页。试卷主要包含了考生必须保证答题卡的整洁,计算,下列说法正确的是,已知,若x<y,则下列式子不成立的是等内容,欢迎下载使用。
甘肃省白银市2022-2023学年数学七下期末达标检测试题含答案: 这是一份甘肃省白银市2022-2023学年数学七下期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,已知正比例函数y=kx等内容,欢迎下载使用。












