

2022-2023学年湖南长沙明德旗舰数学七下期末经典试题含答案
展开2022-2023学年湖南长沙明德旗舰数学七下期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.在![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以点
,以点![]() 为坐标原点建立平面直角坐标系,其中
为坐标原点建立平面直角坐标系,其中![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.式子![]() 有意义,则实数a的取值范围是( )
有意义,则实数a的取值范围是( )
A.a≥-1 B.a≠2 C.a≥-1且a≠2 D.a>2
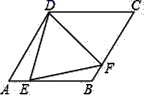
3.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B.![]() C.
C.![]() D.
D.![]()
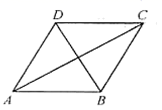
4.如图,已知某广场菱形花坛![]() 的周长是24米,
的周长是24米,![]() ,则此花坛的面积等于( )
,则此花坛的面积等于( )
A.![]() 平方米 B.24平方米 C.
平方米 B.24平方米 C.![]() 平方米 D.
平方米 D.![]() 平方米
平方米
5.将直线y=-2x向上平移5个单位,得到的直线的解析式为( )
A.y=-2x-5 ![]() B.y=-2x+5
B.y=-2x+5 ![]() C.y=-2(x-5)
C.y=-2(x-5) ![]() D.y=-2(x+5)
D.y=-2(x+5)
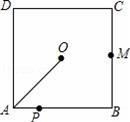
6.如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
A.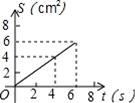 B.
B.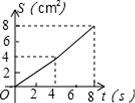
C.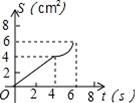 D.
D.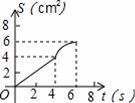
7.以三角形三边中点和三角形三个顶点能画出平行四边形有( )个.
A.1 B.2 C.3 D.4
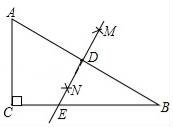
8.如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和N点,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则BE等于( )
AB)为半径作弧,两弧相交于点M和N点,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则BE等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列计算正确的是( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若反比例函数![]() ,在每个象限内y随x的增大而减小,则m的取值范围是( )
,在每个象限内y随x的增大而减小,则m的取值范围是( )
A.m>![]() B.m<
B.m<![]() C.m>一
C.m>一![]() D.m<一
D.m<一![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
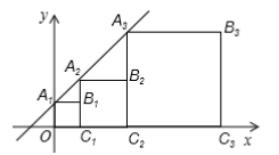
11.正方形![]() 按如图所示的方式放置,点
按如图所示的方式放置,点![]() .和.
.和. ![]() 分别在直线
分别在直线![]() 和x轴上,已知点
和x轴上,已知点![]() ,则Bn的坐标是____________
,则Bn的坐标是____________
12.已知一次函数的图象经过两点![]() ,
,![]() ,则这个函数的表达式为__________.
,则这个函数的表达式为__________.
13.化简![]() 的结果是______
的结果是______
14.已知y+1与x成正比例,则y是x的_____函数.
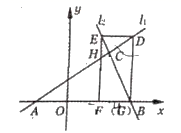
15.如图,已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 相交于点
相交于点![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,矩形
两点,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与
与![]() 点重合,那么
点重合,那么![]() __________________.
__________________.
16. “我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
三、解下列各题(本大题共8小题,共72分)
17.(8分)化简代数式:![]() ,并求当 x=2012 时,代数式的值.
,并求当 x=2012 时,代数式的值.
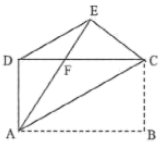
18.(8分)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE,求证:∠DAE=∠ECD.
19.(8分)潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为![]() 元,购买了
元,购买了![]() 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
(1)请求出![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围
的取值范围
(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
20.(8分)作图:如图,平面内有 A,B,C,D 四点 按下列语句画图:
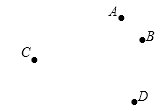
(1)画射线 AB,直线 BC,线段 AC
(2)连接 AD 与 BC 相交于点 E.
21.(8分)如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
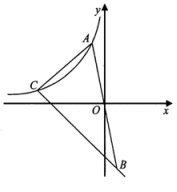
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
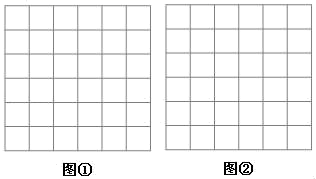
22.(10分)如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,以格点为端点,画线段MN=![]() ;
;
(2)在图②中,以格点为顶点,画正方形ABCD,使它的面积为1.
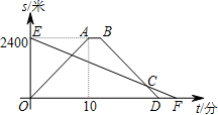
23.(10分)一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
(1)李越骑车的速度为______米/分钟;
(2)B点的坐标为______;
(3)李越从乙地骑往甲地时,s与t之间的函数表达式为______;
(4)王明和李越二人______先到达乙地,先到______分钟.
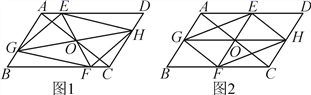
24.(12分)如图1,在▱ABCD中,点O是对角线AC的中点,EF过点O与AD,BC分别相交于点E,F,GH过点O与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有的平行四边形.(四边形AGHD除外)
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、C
5、B
6、A
7、C
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、(2n-1,2n-1)
12、![]()
13、﹣1
14、一次
15、2:5
16、7.1
三、解下列各题(本大题共8小题,共72分)
17、1
18、见解析,
19、 (1)![]() (
(![]() ,且
,且![]() 为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
为整数);(2)当购买电子白板6台,台式电脑18台学校总费用最少钱,最少是108000元.
20、答案见解析
21、(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
22、(1)画图见解析;(2)画图见解析.
23、(1)240;(2)(12,2400);(1)s=240t;(4)李越,1
24、(1)见解析;(2)▱GBCH、▱ABFE、▱EFCD、▱EGFH
2023-2024学年湖南长沙明德旗舰数学九年级第一学期期末综合测试模拟试题含答案: 这是一份2023-2024学年湖南长沙明德旗舰数学九年级第一学期期末综合测试模拟试题含答案,共8页。试卷主要包含了下列计算正确的是等内容,欢迎下载使用。
2023-2024学年湖南省长沙市明德旗舰数学九上期末考试模拟试题含答案: 这是一份2023-2024学年湖南省长沙市明德旗舰数学九上期末考试模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,如图,空心圆柱的俯视图是,若,且,则的值是等内容,欢迎下载使用。
2023-2024学年湖南长沙明德旗舰八上数学期末检测试题含答案: 这是一份2023-2024学年湖南长沙明德旗舰八上数学期末检测试题含答案,共7页。试卷主要包含了已知A,已知是一个完全平方式,则等于,若,则的值为,已知正比例函数y=kx等内容,欢迎下载使用。












