


2022-2023学年湖州市吴兴区数学七下期末质量跟踪监视模拟试题含答案
展开这是一份2022-2023学年湖州市吴兴区数学七下期末质量跟踪监视模拟试题含答案,共8页。
2022-2023学年湖州市吴兴区数学七下期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.甲、乙两台机床同时生产一种零件,在5天中,两台机床每天出次品的数量如下表:
甲 | 0 | 1 | 2 | 0 | 2 |
乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法不正确的是( )
A.甲、乙的平均数相等 B.甲、乙的众数相等
C.甲、乙的中位数相等 D.甲的方差大于乙的方差
2.下列图形中,成中心对称图形的是( )
A.![]() B.
B.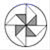 C.
C. D.
D.
3.当![]() 取什么值时,分式
取什么值时,分式![]() 无意义( )
无意义( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.某火车站的显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏正好显示火车班次信息的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列调查中,适合采用全面调查(普查)方式的是( )
A.对巢湖水质情况的调查
B.对端午节期间市场上粽子质量情况的调查
C.节能灯厂家对一批节能灯管使用寿命的调查
D.对某班50名学生视力情况的调查
6.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如图,数轴上的点A所表示的数为x,则x2的值为( )
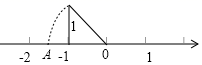
A.2 B.-![]() −10 C.
−10 C.![]() D.-2
D.-2
8.如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
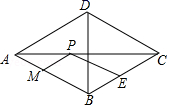
A.6 B.3![]() C.2
C.2![]() D.4.5
D.4.5
9.用配方法解一元二次方程![]() 时,下列变形正确的是( )
时,下列变形正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=![]() 或t=
或t=![]() ,其中正确的结论有( )
,其中正确的结论有( )
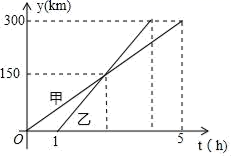
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若关于![]() 的方程
的方程![]() 有实数根,则
有实数根,则![]() 的值可以是_____(写出一个即可)
的值可以是_____(写出一个即可)
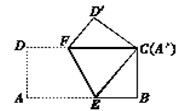
12.如图,将长8cm,宽4cm的矩形ABCD纸片折叠,使点A与C重合,则折痕EF的长为_________cm.
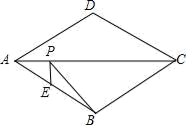
13.如图,菱形ABCD周长为16,∠ADC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_____.
14.将一张A3纸对折并沿折痕裁开,得到2张A4纸.已知A3纸和A4纸是两个相似的矩形,则矩形的短边与长边的比为______.
15.分解因式:![]() .
.
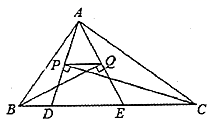
16.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 都在边
都在边![]() 上,
上,![]() 的平分线垂直于
的平分线垂直于![]() ,垂足为
,垂足为![]() ,
,![]() 的平分线垂直于
的平分线垂直于![]() ,垂足为
,垂足为![]() ,则
,则![]() 的长__________.
的长__________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
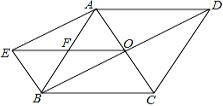
(1)试判断四边形AEBO的形状,并说明你的理由;(2)求证:EO=DC.
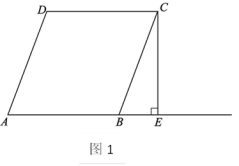
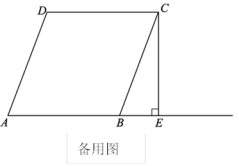
18.(8分)如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.
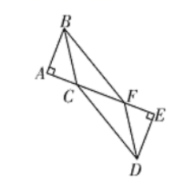
19.(8分)如图:![]() ,点
,点![]() 在一条直线上,
在一条直线上,![]() .求证:四边形
.求证:四边形![]() 是平行四边形.
是平行四边形.
20.(8分)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
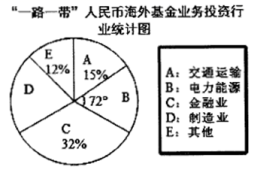
21.(8分) “一路一带”倡议6岁了!到日前为止,中国已与126个国家和29个国际组织签署174份合作文件,共建“一路一带”国家已由亚欧延伸至非洲、拉美、南太等区域.截止2019年一季度末,人民币海外基金业务规模约3000亿元,其投资范围覆盖交通运输、电力能源、金融业和制造业等重要行业,投资行业统计图如图所示.
(1)求投资制造业的基金约为多少亿元?
(2)按照规划,中国将继续对“一路一带”基金增加投入,到2019年三季度末,共增加投入630亿元,假设平均每季度的增长率相等,求平均每季度的增长率是多少?
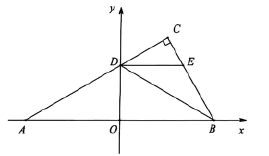
22.(10分)如图平面直角坐标系中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() ,点
,点![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)点![]() 的坐标为 .
的坐标为 .
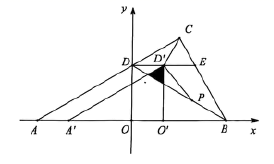
(2)将![]() 沿线段
沿线段![]() 向右平移得
向右平移得![]() ,当点
,当点![]() 与
与![]() 重合时停止运动,记
重合时停止运动,记![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,求
时,求![]() 的最小值;
的最小值;
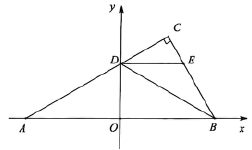
(3)当![]() 移动到点
移动到点![]() 与
与![]() 重合时,将
重合时,将![]() 绕点
绕点![]() 旋转一周,旋转过程中,直线
旋转一周,旋转过程中,直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、点
、点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .当
.当![]() 为直角三角形时,直接写出线段
为直角三角形时,直接写出线段![]() 的长.
的长.
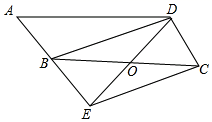
23.(10分)如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)当∠A=50°,∠BOD=100°时,判断四边形BECD的形状,并说明理由.
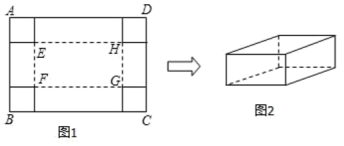
24.(12分)在一张足够大的纸板上截取一个面积为![]() 的矩形纸板
的矩形纸板![]() ,如图
,如图![]() ,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面
,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面![]() 为矩形,如图
为矩形,如图![]() ,设小正方形的边长为
,设小正方形的边长为![]() 厘米.、
厘米.、
(1)若矩形纸板的一个边长为![]() .
.
①当纸盒的底面积为![]() 时,求
时,求![]() 的值;
的值;
②求纸盒的侧面积的最大值;
(2)当![]() ,且侧面积与底面积之比为
,且侧面积与底面积之比为![]() 时,求
时,求![]() 的值.
的值.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、B
5、D
6、D
7、A
8、C
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、4
12、![]()
13、![]() .
.
14、![]()
15、![]() .
.
16、1
三、解下列各题(本大题共8小题,共72分)
17、证明见解析
18、 (1)见解析;(2) AG=DH,理由见解析;(3) 不存在.理由见解析.
19、详见解析
20、3
21、(1)630亿元;(2)10%
22、(1)C(3,3![]() );(3)最小值为3+3
);(3)最小值为3+3![]() ;(3)D3H的值为3
;(3)D3H的值为3![]() -3或3
-3或3![]() +3或1
+3或1![]() -1或1
-1或1![]() +1.
+1.
23、 (1)证明见解析;(2)四边形BECD是矩形.
24、(1)①12;②当![]() 时,
时,![]() ;(2)1
;(2)1
相关试卷
这是一份2023-2024学年浙江省湖州市吴兴区十校联考数学九上期末质量跟踪监视试题含答案,共7页。试卷主要包含了如图,已知,下列事件中为必然事件的是等内容,欢迎下载使用。
这是一份浙江省湖州市南浔区实验学校2022-2023学年七下数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了下列式子中,属于分式的是,下列式子属于最简二次根式的是等内容,欢迎下载使用。
这是一份河南周口港区2022-2023学年数学七下期末质量跟踪监视模拟试题含答案,共6页。












