

北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
展开
这是一份北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共24页。试卷主要包含了已知二次函数满足条件,2+2的过程等内容,欢迎下载使用。
北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
一.一元二次方程的解(共1小题)
1.(2021秋•西城区期末)关于x的一元二次方程x2+mx+4=0有一个根为1,则m的值为 .
二.解一元二次方程-直接开平方法(共1小题)
2.(2022秋•西城区期末)一元二次方程x2﹣16=0的解是 .
三.根的判别式(共1小题)
3.(2022秋•西城区期末)若关于x的一元二次方程x2+3x+c=0有两个相等的实数根,则c的值为 .
四.二次函数的性质(共1小题)
4.(2022秋•西城区期末)已知二次函数满足条件:①图象过原点;②当x>1时,y随x的增大而增大.请你写出一个满足上述条件的二次函数的解析式: .
五.二次函数图象与系数的关系(共1小题)
5.(2020秋•西城区期末)若抛物线y=ax2+bx+c(a≠0)的示意图如图所示,则a 0,b 0,c 0(填“>”,“=”或“<”).
六.二次函数图象上点的坐标特征(共1小题)
6.(2022秋•西城区期末)点M(3,m)是抛物线y=x2﹣x上一点,则m的值是 ,点M关于原点对称的点的坐标是 .
七.二次函数图象与几何变换(共1小题)
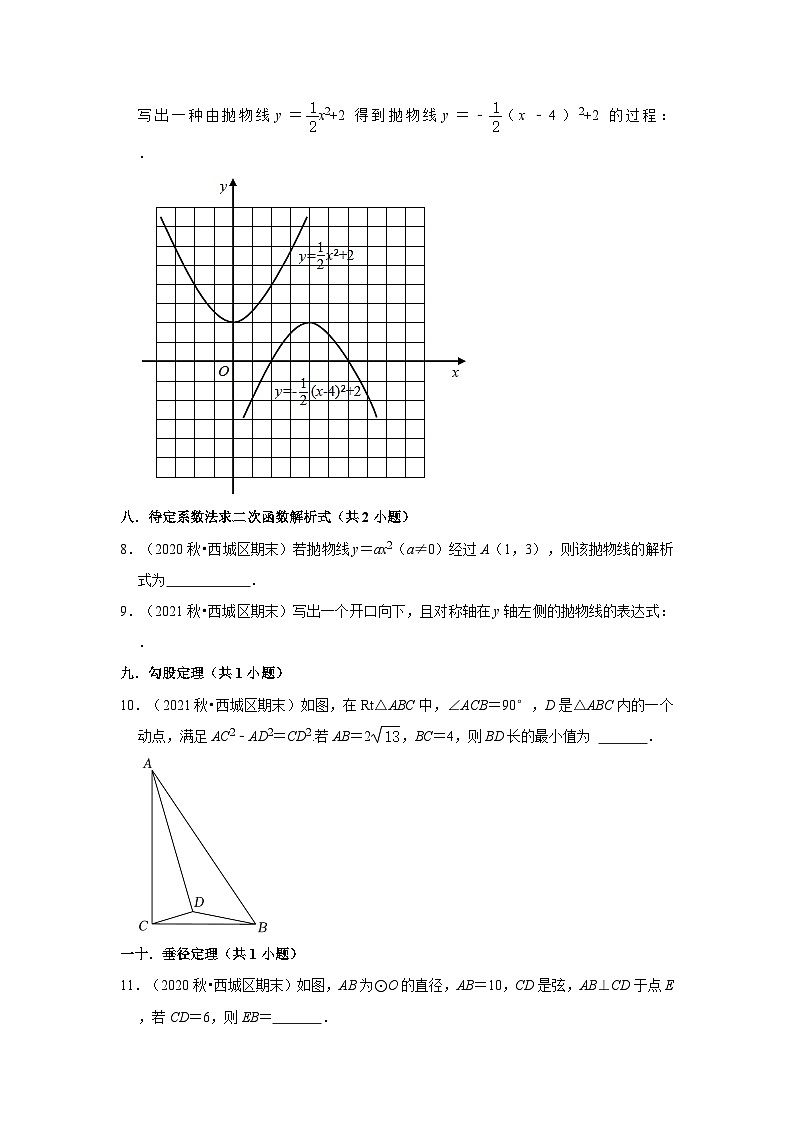
7.(2021秋•西城区期末)如图,在平面直角坐标系xOy中,抛物线y=﹣(x﹣4)2+2可以看作是抛物线y=x2+2经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由抛物线y=x2+2得到抛物线y=﹣(x﹣4)2+2的过程: .
八.待定系数法求二次函数解析式(共2小题)
8.(2020秋•西城区期末)若抛物线y=ax2(a≠0)经过A(1,3),则该抛物线的解析式为 .
9.(2021秋•西城区期末)写出一个开口向下,且对称轴在y轴左侧的抛物线的表达式: .
九.勾股定理(共1小题)
10.(2021秋•西城区期末)如图,在Rt△ABC中,∠ACB=90°,D是△ABC内的一个动点,满足AC2﹣AD2=CD2.若AB=2,BC=4,则BD长的最小值为 .
一十.垂径定理(共1小题)
11.(2020秋•西城区期末)如图,AB为⊙O的直径,AB=10,CD是弦,AB⊥CD于点E,若CD=6,则EB= .
一十一.圆周角定理(共1小题)
12.(2020秋•西城区期末)如图,在平面直角坐标系xOy中,P(4,3),⊙O经过点P.点A,点B在y轴上,PA=PB,延长PA,PB分别交⊙O于点C,点D,设直线CD与x轴正方向所夹的锐角为α.
(1)⊙O的半径为 ;
(2)tanα= .
一十二.点与圆的位置关系(共2小题)
13.(2022秋•西城区期末)已知⊙O的半径为5,点P到圆心O的距离为8,则点P在⊙O (填“内”“上”或“外”).
14.(2022秋•西城区期末)如图,AB是⊙O的直径,C为⊙O上一点,且AB⊥OC,P为圆上一动点,M为AP的中点,连接CM.若⊙O的半径为2,则CM长的最大值是 .
一十三.确定圆的条件(共1小题)
15.(2021秋•西城区期末)如图,在平面直角坐标系xOy中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 .
一十四.切线的性质(共1小题)
16.(2020秋•西城区期末)如图,PA,PB是⊙O的两条切线,A,B为切点,若OA=2,∠APB=60°,则PB= .
一十五.切线的判定(共1小题)
17.(2022秋•西城区期末)如图,在平面直角坐标系xOy中,以点A(,0)为圆心,1为半径画圆.将⊙A绕点O逆时针旋转α(0°<α<180°)得到⊙A',使得⊙A'与y轴相切,则α的度数是 .
一十六.正多边形和圆(共1小题)
18.(2020秋•西城区期末)若正六边形的边长为2,则它的外接圆半径是 .
一十七.弧长的计算(共1小题)
19.(2021秋•西城区期末)如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为160°的圆弧形窗帘轨道(如图2)需用此材料800πmm,则此圆弧所在圆的半径为 mm.
一十八.扇形面积的计算(共1小题)
20.(2022秋•西城区期末)圆心角是60°的扇形的半径为6,则这个扇形的面积是 .
一十九.旋转的性质(共1小题)
21.(2021秋•西城区期末)如图,将△ABC绕点A顺时针旋转α(0°<α<90°)得到△ADE,点B的对应点D恰好落在边BC上,则∠ADE= .(用含α的式子表示)
二十.关于原点对称的点的坐标(共1小题)
22.(2021秋•西城区期末)在平面直角坐标系xOy中,点(4,﹣7)关于原点的对称点坐标为 .
二十一.相似形综合题(共1小题)
23.(2020秋•西城区期末)放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,OD=DA=CB,DC=AB=BE,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
若连接OA,OE,可证得以下结论:
①△ODA和△OCE为等腰三角形,则∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠ );
②四边形ABCD为平行四边形(理由是 );
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 倍得到的.
二十二.锐角三角函数的定义(共1小题)
24.(2020秋•西城区期末)如图,在Rt△ABC中,∠C=90°,AC=6,AB=9,则sinB= .
北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
参考答案与试题解析
一.一元二次方程的解(共1小题)
1.(2021秋•西城区期末)关于x的一元二次方程x2+mx+4=0有一个根为1,则m的值为 ﹣5 .
【答案】﹣5.
【解答】解:把x=1代入方程x2+mx+4=0得1+m+4=0,
解得m=﹣5.
故答案为:﹣5.
二.解一元二次方程-直接开平方法(共1小题)
2.(2022秋•西城区期末)一元二次方程x2﹣16=0的解是 x1=﹣4,x2=4 .
【答案】见试题解答内容
【解答】解:方程变形得:x2=16,
开方得:x=±4,
解得:x1=﹣4,x2=4.
故答案为:x1=﹣4,x2=4
三.根的判别式(共1小题)
3.(2022秋•西城区期末)若关于x的一元二次方程x2+3x+c=0有两个相等的实数根,则c的值为 .
【答案】见试题解答内容
【解答】解:∵一元二次方程x2+3x+c=0有两个相等的实数根,
∴Δ=32﹣4c=0,
解得c=.
故答案为:.
四.二次函数的性质(共1小题)
4.(2022秋•西城区期末)已知二次函数满足条件:①图象过原点;②当x>1时,y随x的增大而增大.请你写出一个满足上述条件的二次函数的解析式: 答案不唯一,如:y=x2﹣2x .
【答案】答案不唯一,如:y=x2﹣2x.
【解答】解:∵当x>1时,y随x的增大而增大,
∴抛物线方程中的二次项系数a>0,对称轴是直线x=1.
∵图象过原点,
∴抛物线方程中的常数项c=0符合题意.
∴答案不唯一,如:y=x2﹣2x.
故答案为:答案不唯一,如:y=x2﹣2x.
五.二次函数图象与系数的关系(共1小题)
5.(2020秋•西城区期末)若抛物线y=ax2+bx+c(a≠0)的示意图如图所示,则a > 0,b < 0,c < 0(填“>”,“=”或“<”).
【答案】>,<,<.
【解答】解:∵抛物线开口方向向上,
∴a>0,
∵对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0.
故答案为>,<,<.
六.二次函数图象上点的坐标特征(共1小题)
6.(2022秋•西城区期末)点M(3,m)是抛物线y=x2﹣x上一点,则m的值是 6 ,点M关于原点对称的点的坐标是 (﹣3,﹣6) .
【答案】6,(﹣3,﹣6).
【解答】解:∵点M(3,m)是抛物线y=x2﹣x上一点,
∴m=32﹣3=6,
∴M(3,6),
∴点M关于原点对称的点的坐标是 (﹣3,﹣6).
故答案为:6,(﹣3,﹣6).
七.二次函数图象与几何变换(共1小题)
7.(2021秋•西城区期末)如图,在平面直角坐标系xOy中,抛物线y=﹣(x﹣4)2+2可以看作是抛物线y=x2+2经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由抛物线y=x2+2得到抛物线y=﹣(x﹣4)2+2的过程: 将抛物线y=x2+2绕顶点(0,2)顺时针方向旋转180度,再向右平移4个单位长度得到抛物线 y=﹣(x﹣4)2+2.(答案不唯一) .
【答案】将抛物线y=x2+2绕顶点(0,2)顺时针方向旋转180度,再向右平移4个单位长度得到抛物线 y=﹣(x﹣4)2+2.(答案不唯一).
【解答】解:抛物线y=x2+2的顶点为(0,2),抛物线y=﹣(x﹣4)2+2的顶点为(4,2),
∴将抛物线y=x2+2绕顶点(0,2)顺时针方向旋转180度,再向右平移4个单位长度得到抛物线 y=﹣(x﹣4)2+2.
故答案为:将抛物线y=x2+2绕顶点(0,2)顺时针方向旋转180度,再向右平移4个单位长度得到抛物线 y=﹣(x﹣4)2+2.(答案不唯一).
八.待定系数法求二次函数解析式(共2小题)
8.(2020秋•西城区期末)若抛物线y=ax2(a≠0)经过A(1,3),则该抛物线的解析式为 y=3x2 .
【答案】y=3x2.
【解答】解:把A(1,3)代入y=ax2(a≠0)中,
得3=a×12,
解得a=3,
所以该抛物线的解析式为y=3x2.
故答案为:y=3x2.
9.(2021秋•西城区期末)写出一个开口向下,且对称轴在y轴左侧的抛物线的表达式: y=﹣x2﹣x,(答案不唯一) .
【答案】y=﹣x2﹣x,(答案不唯一).
【解答】解:∵开口向下,
∴a<0,
∵对称轴在y轴左侧,
∴﹣<0,
∴b<0,
故抛物线的解析式可以为y=﹣x2﹣x,(答案不唯一),
故答案为:y=﹣x2﹣x,(答案不唯一).
九.勾股定理(共1小题)
10.(2021秋•西城区期末)如图,在Rt△ABC中,∠ACB=90°,D是△ABC内的一个动点,满足AC2﹣AD2=CD2.若AB=2,BC=4,则BD长的最小值为 2 .
【答案】2.
【解答】解:取AC的中点H,连接HD,HB,
在Rt△ABC中,由勾股定理得AC=,
∵AC2﹣AD2=CD2.
∴∠ADC=90°,
∵点H为AC的中点,
∴DH=CH=3,
∴BH=,
∵BD≥BH﹣DH,
∴BD的最小值为5﹣3=2,
故答案为:2.
一十.垂径定理(共1小题)
11.(2020秋•西城区期末)如图,AB为⊙O的直径,AB=10,CD是弦,AB⊥CD于点E,若CD=6,则EB= 1 .
【答案】1.
【解答】解:连接OC,如图所示:
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3,
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=AB=5,
∴OE==4,
∴BE=OB﹣OE=AB﹣OE=5﹣4=1,
故答案为:1.
一十一.圆周角定理(共1小题)
12.(2020秋•西城区期末)如图,在平面直角坐标系xOy中,P(4,3),⊙O经过点P.点A,点B在y轴上,PA=PB,延长PA,PB分别交⊙O于点C,点D,设直线CD与x轴正方向所夹的锐角为α.
(1)⊙O的半径为 5 ;
(2)tanα= .
【答案】(1)5.
(2)
【解答】解:(1)连接OP.
∵P(4,3),
∴OP==5,
故答案为:5.
(2)设CD交x轴于J,过点P作PT⊥AB交⊙O于T,交AB于E,连接CT,DT,OT.
∵P(4,3),
∴PE=4,OE=3,
在Rt△OPE中,tan∠POE==,
∵OE⊥PT,OP=OT,
∴∠POE=∠TOE,
∴∠PDT=∠POT=∠POE,
∵PA=PB.PE⊥AB,
∴∠APT=∠DPT,
∴=,
∴∠TDC=∠TCD,
∵PT∥x轴,
∴∠CJO=∠CKP,
∵∠CKP=∠TCK+∠CTK,∠CTP=∠CDP,∠PDT=∠TDC+∠CDP,
∴∠TDP=∠CJO,
∴∠CJO=∠POE,
∴tan∠CJO=tan∠POE=.
补充方法:证明∠CJO=∠EOP时,可以这样证明:∵∠CJO+∠TOJ=90°,∠TOJ+∠EOT=90°,
∴∠CJO=∠EOT,
∵∠EOT=∠EOB,
∴∠CJO=∠EOP,可得结论.
故答案为:.
一十二.点与圆的位置关系(共2小题)
13.(2022秋•西城区期末)已知⊙O的半径为5,点P到圆心O的距离为8,则点P在⊙O 外 (填“内”“上”或“外”).
【答案】外.
【解答】解:∵⊙O的半径为5,点P到圆心O的距离为8,8>5,
∴点P在⊙O外,
故答案为:外.
14.(2022秋•西城区期末)如图,AB是⊙O的直径,C为⊙O上一点,且AB⊥OC,P为圆上一动点,M为AP的中点,连接CM.若⊙O的半径为2,则CM长的最大值是 .
【答案】+1.
【解答】解:如图,当点P在⊙O上移动时,AP的中点M的轨迹是以OA为直径的⊙O′,
因此CO′交⊙O′于点M,此时CM的值最大,
由题意得,OA=OB=OC=2,OO′=OA=1=O′M,
在Rt△O′OC中,OC=2,OO′=1,
∴O′C==,
∴CM=CO′+O′M=+1,
故答案为:+1.
一十三.确定圆的条件(共1小题)
15.(2021秋•西城区期末)如图,在平面直角坐标系xOy中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 (2,1) .
【答案】(2,1).
【解答】解:从图形可知:A点的坐标是(0,2),B点的坐标是(1,3),C点的坐标是(3,3),
连接AB,作线段AB和线段BC的垂直平分线MN、EF,两线交于Q,则Q是圆弧的圆心,如图,
∴Q点的坐标是(2,1),
故答案为:(2,1).
一十四.切线的性质(共1小题)
16.(2020秋•西城区期末)如图,PA,PB是⊙O的两条切线,A,B为切点,若OA=2,∠APB=60°,则PB= 2 .
【答案】2.
【解答】解:∵PA、PB是⊙O的两条切线,∠APB=60°,OA=OB=2,
∴∠BPO=∠APB=30°,BO⊥PB.
∴PO=2AO=4,
∴PB===2.
故答案为:2.
一十五.切线的判定(共1小题)
17.(2022秋•西城区期末)如图,在平面直角坐标系xOy中,以点A(,0)为圆心,1为半径画圆.将⊙A绕点O逆时针旋转α(0°<α<180°)得到⊙A',使得⊙A'与y轴相切,则α的度数是 45°或135° .
【答案】45°或135°.
【解答】解:如图1,点A′在第一象限,设⊙A′与y轴相切于点B,连接OA′、BA′,
∵OB⊥A′B,
∴∠A′BO=90°,
∵⊙A的半径为1,A(,0),
∴OA=,
由旋转得OA′=OA=,
∵⊙A的半径为1,
∴A′B=1,
∴OB===1,
∴A′B=OB,
∴∠BOA′=∠BA′O=45°,
∴α=∠AOA′=90°﹣45°=45°;
如图2,点A′在第二象限,设⊙A′与y轴相切于点C,连接OA′、CA′,
∵OC⊥A′C,
∴∠A′CO=90°,
∵OA′=OA=,AC=1,
∴OC===1,
∴A′C=OC,
∴∠COA′=∠CA′O=45°,
∴α=∠AOA′=90°+45°=135°,
故答案为:45°或135°.
一十六.正多边形和圆(共1小题)
18.(2020秋•西城区期末)若正六边形的边长为2,则它的外接圆半径是 2 .
【答案】见试题解答内容
【解答】解:如图所示,连接OB、OC;
∵此六边形是正六边形,
∴∠BOC==60°,
∵OB=OC,
∴△BOC是等边三角形,
∴OB=OC=BC=2.
故答案为:2.
一十七.弧长的计算(共1小题)
19.(2021秋•西城区期末)如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为160°的圆弧形窗帘轨道(如图2)需用此材料800πmm,则此圆弧所在圆的半径为 900 mm.
【答案】900.
【解答】解:设此圆弧所在圆的半径为Rmm,
由弧长公式得:=800π,
解得:R=900,
即此圆弧所在圆的半径为900mm,
故答案为:900.
一十八.扇形面积的计算(共1小题)
20.(2022秋•西城区期末)圆心角是60°的扇形的半径为6,则这个扇形的面积是 6π .
【答案】见试题解答内容
【解答】解:该扇形的面积S==6π.
故答案为:6π.
一十九.旋转的性质(共1小题)
21.(2021秋•西城区期末)如图,将△ABC绕点A顺时针旋转α(0°<α<90°)得到△ADE,点B的对应点D恰好落在边BC上,则∠ADE= 90°﹣ .(用含α的式子表示)
【答案】90°﹣.
【解答】解:由旋转的性质可知,AD=AB,∠ADE=∠B,
∴∠ADB=∠B,
∵∠BAD=α,
∴∠ADE=∠ADB==90°﹣,
故答案为:90°﹣.
二十.关于原点对称的点的坐标(共1小题)
22.(2021秋•西城区期末)在平面直角坐标系xOy中,点(4,﹣7)关于原点的对称点坐标为 (﹣4,7) .
【答案】(﹣4,7).
【解答】解:在平面直角坐标系xOy中,点(4,﹣7)关于原点的对称点坐标为(﹣4,7),
故答案为:(﹣4,7).
二十一.相似形综合题(共1小题)
23.(2020秋•西城区期末)放缩尺是一种绘图工具,它能把图形放大或缩小.
制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点,OD=DA=CB,DC=AB=BE,在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
若连接OA,OE,可证得以下结论:
①△ODA和△OCE为等腰三角形,则∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠ OCE );
②四边形ABCD为平行四边形(理由是 两组对边分别相等的四边形是平行四边形 );
③∠DOA=∠COE,于是可得O,A,E三点在一条直线上;
④当时,图形N是以点O为位似中心,把图形M放大为原来的 倍得到的.
【答案】OCE;两组对边分别相等的四边形是平行四边形;.
【解答】解:①∵△ODA和△OCE为等腰三角形,
∴∠DOA=(180°﹣∠ODA),∠COE=(180°﹣∠OCE);
②∵AD=BC,DC=AB,
∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形);
③连接OA,AE,
∵∠DOA=∠COE,
∴O,A,E三点在一条直线上;
④∵=,
∴设CD=AB=BE=3x,OD=AD=BC=5x,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AOD∽△EOC,
∴==,
∴图形N是以点O为位似中心,把图形M放大为原来的,
故答案为:OCE;两组对边分别相等的四边形是平行四边形;.
二十二.锐角三角函数的定义(共1小题)
24.(2020秋•西城区期末)如图,在Rt△ABC中,∠C=90°,AC=6,AB=9,则sinB= .
【答案】.
【解答】解:在Rt△ABC中,∠C=90°,AC=6,AB=9,
则sinB===,
故答案为:.
相关试卷
这是一份北京市通州区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共22页。试卷主要包含了图象上一点,如图,A,B,C为⊙O上的点等内容,欢迎下载使用。
这是一份北京市石景山区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共21页。试卷主要包含了为W等内容,欢迎下载使用。
这是一份北京市密云区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共20页。试卷主要包含了如图,抛物线y=﹣x2+2等内容,欢迎下载使用。








