湖南省益阳市2021-2023三年中考数学真题分类汇编-01选择题知识点分类

这是一份湖南省益阳市2021-2023三年中考数学真题分类汇编-01选择题知识点分类，共23页。
湖南省益阳市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
一．正数和负数（共1小题）
1．（2022•益阳）四个实数﹣，1，2，中，比0小的数是（　　）
A．﹣ B．1 C．2 D．
二．相反数（共1小题）
2．（2021•益阳）﹣2021的相反数等于（　　）
A．2021 B．﹣2021 C． D．﹣
三．实数大小比较（共1小题）
3．（2023•益阳）四个实数﹣，0，2，中，最大的数是（　　）
A．﹣ B．0 C．2 D．
四．同底数幂的除法（共2小题）
4．（2023•益阳）下列计算正确的是（　　）
A．x2•x3＝x6 B．（x3）2＝x5 C．（3x）2＝6x2 D．x3÷x＝x2
5．（2022•益阳）下列各式中，运算结果等于a2的是（　　）
A．a3﹣a B．a+a C．a•a D．a6÷a3
五．单项式乘单项式（共1小题）
6．（2021•益阳）已知a≠0，下列运算正确的是（　　）
A．3a﹣2a＝1 B．3a•2a＝6a C．a3÷a2＝a D．（2a）3＝6a3
六．提公因式法与公式法的综合运用（共1小题）
7．（2023•益阳）下列因式分解正确的是（　　）
A．2a2﹣4a+2＝2（a﹣1）2 B．a2+ab+a＝a（a+b）
C．4a2﹣b2＝（4a+b）（4a﹣b） D．a3b﹣ab3＝ab（a﹣b）2
七．最简二次根式（共1小题）
8．（2021•益阳）将化为最简二次根式，其结果是（　　）
A． B． C． D．
八．解二元一次方程组（共1小题）
9．（2021•益阳）解方程组时，若将①﹣②可得（　　）
A．﹣2y＝﹣1 B．﹣2y＝1 C．4y＝1 D．4y＝﹣1
九．由实际问题抽象出二元一次方程组（共1小题）
10．（2023•益阳）某学校为进一步开展好劳动教育实践活动，用1580元购进A，B两种劳动工具共145件，A，B两种劳动工具每件分别为10元，12元．设购买A，B两种劳动工具的件数分别为x，y，那么下面列出的方程组中正确的是（　　）
A． B．
C． D．
一十．根与系数的关系（共1小题）
11．（2022•益阳）若x＝﹣1是方程x2+x+m＝0的一个根，则此方程的另一个根是（　　）
A．﹣1 B．0 C．1 D．2
一十一．解一元一次不等式组（共2小题）
12．（2023•益阳）将不等式组的解集在数轴上表示，正确的是（　　）
A． B．
C． D．
13．（2022•益阳）若x＝2是下列四个选项中的某个不等式组的一个解，则这个不等式组是（　　）
A． B． C． D．
一十二．函数关系式（共1小题）
14．（2022•益阳）已知一个函数的因变量y与自变量x的几组对应值如表，则这个函数的表达式可以是（　　）
x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…
A．y＝2x B．y＝x﹣1 C．y＝ D．y＝x2
一十三．动点问题的函数图象（共1小题）
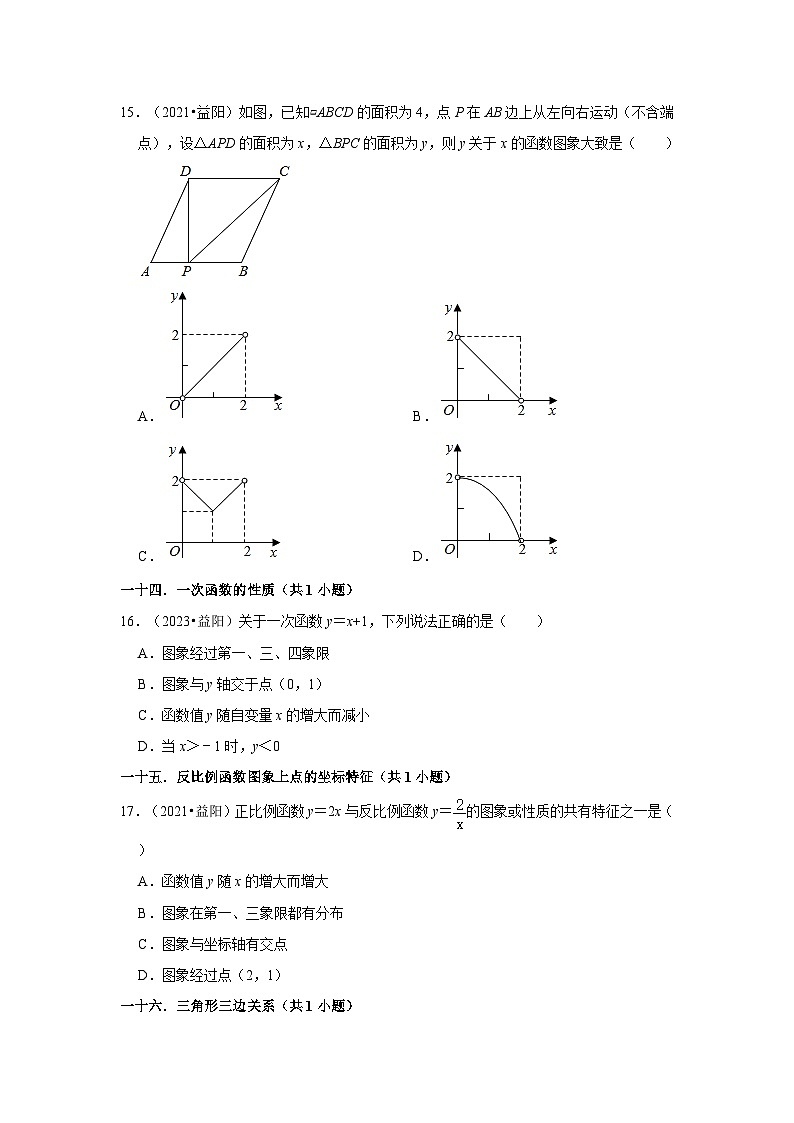
15．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（　　）

A． B．
C． D．
一十四．一次函数的性质（共1小题）
16．（2023•益阳）关于一次函数y＝x+1，下列说法正确的是（　　）
A．图象经过第一、三、四象限
B．图象与y轴交于点（0，1）
C．函数值y随自变量x的增大而减小
D．当x＞﹣1时，y＜0
一十五．反比例函数图象上点的坐标特征（共1小题）
17．（2021•益阳）正比例函数y＝2x与反比例函数y＝的图象或性质的共有特征之一是（　　）
A．函数值y随x的增大而增大
B．图象在第一、三象限都有分布
C．图象与坐标轴有交点
D．图象经过点（2，1）
一十六．三角形三边关系（共1小题）
18．（2022•益阳）如图1所示，将长为6的矩形纸片沿虚线折成3个矩形，其中左右两侧矩形的宽相等，若要将其围成如图2所示的三棱柱形物体，则图中a的值可以是（　　）

A．1 B．2 C．3 D．4
一十七．等边三角形的性质（共1小题）
19．（2021•益阳）如图，AB∥CD，△ACE为等边三角形，∠DCE＝40°，则∠EAB等于（　　）

A．40° B．30° C．20° D．15°
一十八．平行四边形的性质（共1小题）
20．（2023•益阳）如图，▱ABCD的对角线AC，BD交于点O，下列结论一定成立的是（　　）

A．OA＝OB B．OA⊥OB C．OA＝OC D．∠OBA＝∠OBC
一十九．平行四边形的判定与性质（共1小题）
21．（2022•益阳）如图，在▱ABCD中，AB＝8，点E是AB上一点，AE＝3，连接DE，过点C作CF∥DE，交AB的延长线于点F，则BF的长为（　　）

A．5 B．4 C．3 D．2
二十．作图—基本作图（共2小题）
22．（2022•益阳）如图，在△ABC中，BD平分∠ABC，以点A为圆心，以任意长为半径画弧交射线AB，AC于两点，分别以这两点为圆心，以适当的定长为半径画弧，两弧交于点E，作射线AE，交BD于点I，连接CI，以下说法错误的是（　　）

A．I到AB，AC边的距离相等
B．CI平分∠ACB
C．I是△ABC的内心
D．I到A，B，C三点的距离相等
23．（2021•益阳）如图，在△ABC中，AC＞BC，分别以点A，B为圆心，以大于AB的长为半径画弧，两弧交于D，E，经过D，E作直线分别交AB，AC于点M，N，连接BN，下列结论正确的是（　　）

A．AN＝NC B．AN＝BN C．MN＝BC D．BN平分∠ABC
二十一．轴对称图形（共1小题）
24．（2023•益阳）如图所示正方体的展开图中，是轴对称图形的是（　　）
A． B．
C． D．
二十二．旋转的性质（共1小题）
25．（2022•益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（　　）

A．①②③ B．①②④ C．①③④ D．②③④
二十三．中心对称图形（共1小题）
26．（2021•益阳）以下有关勾股定理证明的图形中，不是中心对称图形的是（　　）
A． B．
C． D．
二十四．解直角三角形（共1小题）
27．（2023•益阳）如图，在平面直角坐标系xOy中，有三点A（0，1），B（4，1），C（5，6），则sin∠BAC＝（　　）

A． B． C． D．
二十五．加权平均数（共1小题）
28．（2021•益阳）小刘利用空闲时间到外地某建筑公司打工，公司承诺：正常上班的工资为200元/天，不能正常上班（如下雨）的工资为80元/天，如果某月（30天）正常上班的天数占80%，则当月小刘的日平均工资为（　　）
A．140元 B．160元 C．176元 D．182元
二十六．方差（共1小题）
29．（2023•益阳）乡村医生李医生在对本村老年人进行年度免费体检时，发现张奶奶血压偏高，为了准确诊断，随后7天，李医生每天定时为张奶奶测量血压，测得数据如下表：
测量时间
第1天
第2天
第3天
第4天
第5天
第6天
第7天
收缩压（毫米汞柱）
151
148
140
139
140
136
140
舒张压（毫米汞柱）
90
92
88
88
90
80
88
对收缩压，舒张压两组数据分别进行统计分析，其中错误的是（　　）
A．收缩压的中位数为139 B．舒张压的众数为88
C．收缩压的平均数为142 D．舒张压的方差为
二十七．概率公式（共1小题）
30．（2022•益阳）在某市组织的物理实验操作考试中，考试所用实验室共有24个测试位，分成6组，同组4个测试位各有一道相同试题，各组的试题不同，分别标记为A，B，C，D，E，F，考生从中随机抽取一道试题，则某个考生抽到试题A的概率为（　　）
A． B． C． D．

湖南省益阳市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
参考答案与试题解析
一．正数和负数（共1小题）
1．（2022•益阳）四个实数﹣，1，2，中，比0小的数是（　　）
A．﹣ B．1 C．2 D．
【答案】A
【解答】解：根据负数都小于零可得，﹣＜0．
故选：A．
二．相反数（共1小题）
2．（2021•益阳）﹣2021的相反数等于（　　）
A．2021 B．﹣2021 C． D．﹣
【答案】A
【解答】解：﹣2021的相反数是2021，
故选：A．
三．实数大小比较（共1小题）
3．（2023•益阳）四个实数﹣，0，2，中，最大的数是（　　）
A．﹣ B．0 C．2 D．
【答案】C
【解答】解：∵﹣＜0＜＜2，
∴在实数﹣，0，2，中，最大的数是2，
故选：C．
四．同底数幂的除法（共2小题）
4．（2023•益阳）下列计算正确的是（　　）
A．x2•x3＝x6 B．（x3）2＝x5 C．（3x）2＝6x2 D．x3÷x＝x2
【答案】D
【解答】解：A．x2•x3＝x5，故A不符合题意；
B．（x3）2＝x6，故B不符合题意；
C．（3x）2＝9x2，故C不符合题意；
D．x3÷x＝x2，故D符合题意；
故选：D．
5．（2022•益阳）下列各式中，运算结果等于a2的是（　　）
A．a3﹣a B．a+a C．a•a D．a6÷a3
【答案】C
【解答】解：A、∵a3与a不是同类项，不能进行合并运算，∴选项A不符合题意；
B、∵a+a＝2a，∴选项B不符合题意；
C、∵a•a＝a2，∴选项C符合题意；
D、∵a6÷a3＝a3，∴选项D不符合题意．
故选：C．
五．单项式乘单项式（共1小题）
6．（2021•益阳）已知a≠0，下列运算正确的是（　　）
A．3a﹣2a＝1 B．3a•2a＝6a C．a3÷a2＝a D．（2a）3＝6a3
【答案】C
【解答】解：A．3a﹣2a＝a，故此选项不合题意；
B．3a•2a＝6a2，故此选项不合题意；
C．a3÷a2＝a，故此选项符合题意；
D．（2a）3＝8a3，故此选项不合题意；
故选：C．
六．提公因式法与公式法的综合运用（共1小题）
7．（2023•益阳）下列因式分解正确的是（　　）
A．2a2﹣4a+2＝2（a﹣1）2 B．a2+ab+a＝a（a+b）
C．4a2﹣b2＝（4a+b）（4a﹣b） D．a3b﹣ab3＝ab（a﹣b）2
【答案】A
【解答】解：A选项，2a2﹣4a+2＝2（a﹣1）2，故该选项符合题意；
B选项，a2+ab+a＝a（a+b+1），故该选项不符合题意；
C选项，4a2﹣b2＝（2a+b）（2a﹣b），故该选项不符合题意；
D选项，a3b﹣ab3＝ab（a2﹣b2）＝ab（a+b）（a﹣b），故该选项不符合题意．
故选：A．
七．最简二次根式（共1小题）
8．（2021•益阳）将化为最简二次根式，其结果是（　　）
A． B． C． D．
【答案】D
【解答】解：＝＝，
故选：D．
八．解二元一次方程组（共1小题）
9．（2021•益阳）解方程组时，若将①﹣②可得（　　）
A．﹣2y＝﹣1 B．﹣2y＝1 C．4y＝1 D．4y＝﹣1
【答案】D
【解答】解：，
①﹣②，得4y＝﹣1，
故选：D．
九．由实际问题抽象出二元一次方程组（共1小题）
10．（2023•益阳）某学校为进一步开展好劳动教育实践活动，用1580元购进A，B两种劳动工具共145件，A，B两种劳动工具每件分别为10元，12元．设购买A，B两种劳动工具的件数分别为x，y，那么下面列出的方程组中正确的是（　　）
A． B．
C． D．
【答案】A
【解答】解：∵购进A，B两种劳动工具共145件，
∴x+y＝145；
∵A，B两种劳动工具每件分别为10元，12元．且购买这批劳动工具共花费1580元，
∴10x+12y＝1580，
∴根据题意可列出方程组．
故选：A．
一十．根与系数的关系（共1小题）
11．（2022•益阳）若x＝﹣1是方程x2+x+m＝0的一个根，则此方程的另一个根是（　　）
A．﹣1 B．0 C．1 D．2
【答案】B
【解答】解：设x2+x+m＝0另一个根是α，
∴﹣1+α＝﹣1，
∴α＝0，
故选：B．
一十一．解一元一次不等式组（共2小题）
12．（2023•益阳）将不等式组的解集在数轴上表示，正确的是（　　）
A． B．
C． D．
【答案】B
【解答】解：由x＝2≤0得x≤2，又x＞0，
则不等式组的解集为0＜x≤2．
A项代表0≤x＜2；
B项代表0＜x≤2；
C代表x＜0且x≥2；
D代表x＞0．
故选：B．
13．（2022•益阳）若x＝2是下列四个选项中的某个不等式组的一个解，则这个不等式组是（　　）
A． B． C． D．
【答案】D
【解答】解：A、∵不等式组的解集为x＜﹣1，∴x＝2不在这个范围内，故A不符合题意；
B、∵不等式组的解集为﹣1＜x＜1，∴x＝2不在这个范围内，故B不符合题意；
C、∵不等式组无解，∴x＝2不在这个范围内，故C不符合题意；
D、∵不等式组的解集为x＞1，∴x＝2在这个范围内，故D符合题意．
故选：D．
一十二．函数关系式（共1小题）
14．（2022•益阳）已知一个函数的因变量y与自变量x的几组对应值如表，则这个函数的表达式可以是（　　）
x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…
A．y＝2x B．y＝x﹣1 C．y＝ D．y＝x2
【答案】A
【解答】解：根据表中数据可以看出：y的值是x值的2倍．
∴y＝2x．
故选：A．
一十三．动点问题的函数图象（共1小题）
15．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（　　）

A． B．
C． D．
【答案】B
【解答】解：∵▱ABCD的面积为4，x+y是平行四边形面积的一半，
∴x+y＝2，
∴y＝2﹣x，
∴y是x的一次函数，
且当x＝0时，y＝2；x＝2时，y＝0；
故只有选项B符合题意．
故选：B．
一十四．一次函数的性质（共1小题）
16．（2023•益阳）关于一次函数y＝x+1，下列说法正确的是（　　）
A．图象经过第一、三、四象限
B．图象与y轴交于点（0，1）
C．函数值y随自变量x的增大而减小
D．当x＞﹣1时，y＜0
【答案】B
【解答】解：∵一次函数y＝x+1中，k＞0，b＞0，
∴图象经过第一、二、三象限，
故A不正确；
当x＝0时，y＝1，
∴图象与y轴交于点（0，1），
故B正确；
∵一次函数y＝x+1中，k＞0，
∴函数值y随自变量x的增大而增大，
故C不正确；
∵当x＝﹣1时，y＝0，函数值y随自变量x的增大而增大，
∴当x＞﹣1时，y＞0，
故D不正确；
故选：B．
一十五．反比例函数图象上点的坐标特征（共1小题）
17．（2021•益阳）正比例函数y＝2x与反比例函数y＝的图象或性质的共有特征之一是（　　）
A．函数值y随x的增大而增大
B．图象在第一、三象限都有分布
C．图象与坐标轴有交点
D．图象经过点（2，1）
【答案】B
【解答】解：∵对于正比例函数y＝2x，2＞0，函数值y随x的增大而增大，
对于反比例函数y＝，2＞0，双曲线在每一象限内函数值y随x的增大而减小，
∴A选项不符合题意；
∵对于正比例函数y＝2x，2＞0，直线y＝2x经过第一、三象限，
对于反比例函数y＝，2＞0，双曲线的两个分支在第一、三象限，
∴B选项符合题意；
∵对于正比例函数y＝2x，它的图象经过原点，
对于反比例函数y＝，它的图象与坐标轴没有交点，
∴C选项不符合题意；
∵当x＝2，y＝2×2＝4≠1
∴正比例函数y＝2x的图象不经过点（2，1）．
∵当x＝2时，y＝，
∴反比例函数y＝的图象经过（2，1），
∴D选项不符合题意．
综上，正确选项为：B．
故选：B．
一十六．三角形三边关系（共1小题）
18．（2022•益阳）如图1所示，将长为6的矩形纸片沿虚线折成3个矩形，其中左右两侧矩形的宽相等，若要将其围成如图2所示的三棱柱形物体，则图中a的值可以是（　　）

A．1 B．2 C．3 D．4
【答案】B
【解答】解：长为6的线段围成等腰三角形的腰长为a．则底边长为6﹣2a．
由题意得，．
解得＜a＜3．
所给选项中分别为：1，2，3，4．
∴只有2符合上面不等式组的解集．
∴a只能取2．
故选：B．
一十七．等边三角形的性质（共1小题）
19．（2021•益阳）如图，AB∥CD，△ACE为等边三角形，∠DCE＝40°，则∠EAB等于（　　）

A．40° B．30° C．20° D．15°
【答案】C
【解答】解：∵AB∥CD，
∴∠DCA+∠CAB＝180°，即∠DCE+∠ECA+∠EAC+∠EAB＝180°，
∵△ACE为等边三角形，
∴∠ECA＝∠EAC＝60°，
∴∠EAB＝180°﹣40°﹣60°﹣60°＝20°．
故选：C．
一十八．平行四边形的性质（共1小题）
20．（2023•益阳）如图，▱ABCD的对角线AC，BD交于点O，下列结论一定成立的是（　　）

A．OA＝OB B．OA⊥OB C．OA＝OC D．∠OBA＝∠OBC
【答案】C
【解答】解：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
故选：C．
一十九．平行四边形的判定与性质（共1小题）
21．（2022•益阳）如图，在▱ABCD中，AB＝8，点E是AB上一点，AE＝3，连接DE，过点C作CF∥DE，交AB的延长线于点F，则BF的长为（　　）

A．5 B．4 C．3 D．2
【答案】C
【解答】解：在▱ABCD中，AB＝8，
∴CD＝AB＝8，AB∥CD，
∵AE＝3，
∴BE＝AB﹣AE＝5，
∵CF∥DE，
∴四边形DEFC是平行四边形，
∴DC＝EF＝8，
∴BF＝EF﹣BE＝8﹣5＝3．
故选：C．
二十．作图—基本作图（共2小题）
22．（2022•益阳）如图，在△ABC中，BD平分∠ABC，以点A为圆心，以任意长为半径画弧交射线AB，AC于两点，分别以这两点为圆心，以适当的定长为半径画弧，两弧交于点E，作射线AE，交BD于点I，连接CI，以下说法错误的是（　　）

A．I到AB，AC边的距离相等
B．CI平分∠ACB
C．I是△ABC的内心
D．I到A，B，C三点的距离相等
【答案】D
【解答】解：由作图可知，AE是∠BAC的平分线，
∴I到AB，AC边的距离相等，故选项A正确，不符合题意；
∵BD平分∠ABC，三角形三条角平分线交于一点，
∴CI平分∠ACB，故选项B正确，不符合题意；
I是△ABC的内心，故选项C正确，不符合题意，
∴I到AB，AC，BC的距离相等，不是到A，B，C三点的距离相等，故选项D错误，符合题意；
故选：D．
23．（2021•益阳）如图，在△ABC中，AC＞BC，分别以点A，B为圆心，以大于AB的长为半径画弧，两弧交于D，E，经过D，E作直线分别交AB，AC于点M，N，连接BN，下列结论正确的是（　　）

A．AN＝NC B．AN＝BN C．MN＝BC D．BN平分∠ABC
【答案】B
【解答】解：由作法得DE垂直平分AB，
∴NA＝NB．
故选：B．
二十一．轴对称图形（共1小题）
24．（2023•益阳）如图所示正方体的展开图中，是轴对称图形的是（　　）
A． B．
C． D．
【答案】D
【解答】解：由轴对称图形定义可知D选项中的图形是轴对称图形，
故选：D．
二十二．旋转的性质（共1小题）
25．（2022•益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（　　）

A．①②③ B．①②④ C．①③④ D．②③④
【答案】B
【解答】解：①∵△ABC绕A点逆时针旋转50°得到△AB′C′，
∴BC＝B′C′．故①正确；
②∵△ABC绕A点逆时针旋转50°，
∴∠BAB′＝50°．
∵∠CAB＝20°，
∴∠B′AC＝∠BAB′﹣∠CAB＝30°．
∵∠AB′C′＝∠ABC＝30°，
∴∠AB′C′＝∠B′AC．
∴AC∥C′B′．故②正确；
③在△BAB′中，
AB＝AB′，∠BAB′＝50°，
∴∠AB′B＝∠ABB′＝（180°﹣50°）＝65°．
∴∠BB′C′＝∠AB′B+∠AB′C′＝65°+30°＝95°．
∴C′B′与BB′不垂直．故③不正确；
④在△ACC′中，
AC＝AC′，∠CAC′＝50°，
∴∠ACC′＝（180°﹣50°）＝65°．
∴∠ABB′＝∠ACC′．故④正确．
∴①②④这三个结论正确．
故选：B．
二十三．中心对称图形（共1小题）
26．（2021•益阳）以下有关勾股定理证明的图形中，不是中心对称图形的是（　　）
A． B．
C． D．
【答案】A
【解答】解：A．不是中心对称图形，符合题意；
B．是中心对称图形，不符合题意；
C．是中心对称图形，不符合题意；
D．是中心对称图形，不符合题意．
故选：A．
二十四．解直角三角形（共1小题）
27．（2023•益阳）如图，在平面直角坐标系xOy中，有三点A（0，1），B（4，1），C（5，6），则sin∠BAC＝（　　）

A． B． C． D．
【答案】C
【解答】解：过C作CD⊥AB交AB延长线于D，
∵A（0，1），B（4，1），C（5，6），
∴D（5，1），
∴CD＝6﹣1＝5，AD＝5，
∴AC＝5，
∴sin∠BAC＝＝，
故选：C．

二十五．加权平均数（共1小题）
28．（2021•益阳）小刘利用空闲时间到外地某建筑公司打工，公司承诺：正常上班的工资为200元/天，不能正常上班（如下雨）的工资为80元/天，如果某月（30天）正常上班的天数占80%，则当月小刘的日平均工资为（　　）
A．140元 B．160元 C．176元 D．182元
【答案】C
【解答】解：[200×30×80%+80×30×（1﹣80%）]÷30
＝（4800+480）÷30
＝176（元），
故选：C．
二十六．方差（共1小题）
29．（2023•益阳）乡村医生李医生在对本村老年人进行年度免费体检时，发现张奶奶血压偏高，为了准确诊断，随后7天，李医生每天定时为张奶奶测量血压，测得数据如下表：
测量时间
第1天
第2天
第3天
第4天
第5天
第6天
第7天
收缩压（毫米汞柱）
151
148
140
139
140
136
140
舒张压（毫米汞柱）
90
92
88
88
90
80
88
对收缩压，舒张压两组数据分别进行统计分析，其中错误的是（　　）
A．收缩压的中位数为139 B．舒张压的众数为88
C．收缩压的平均数为142 D．舒张压的方差为
【答案】A
【解答】解：把7天的收缩压从小到大排列，排在中间的数是140，故中位数是140，故选项A符合题意；
在7天的舒张压中，88出现的次数最多，所以舒张压的众数为88，故选项B不符合题意；
收缩压的平均数为：（151+148+140+139+140+136+140）＝142，故选项C不符合题意；
舒张压的平均数为（90+92+88+88+90+80+88）＝88，
舒张压的平均数为[2×（90﹣88）2+（92﹣88）2+（80﹣88）2+3×（88﹣88）2＝，故选项D不符合题意．
故选：A．
二十七．概率公式（共1小题）
30．（2022•益阳）在某市组织的物理实验操作考试中，考试所用实验室共有24个测试位，分成6组，同组4个测试位各有一道相同试题，各组的试题不同，分别标记为A，B，C，D，E，F，考生从中随机抽取一道试题，则某个考生抽到试题A的概率为（　　）
A． B． C． D．
【答案】C
【解答】解：总共有24道题，试题A共有4道，
P（抽到试题A）＝＝，
故选：C．