山东省济南市2021-2023三年中考数学真题分类汇编-02填空题知识点分类

这是一份山东省济南市2021-2023三年中考数学真题分类汇编-02填空题知识点分类，共16页。试卷主要包含了因式分解等内容，欢迎下载使用。
山东省济南市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一．估算无理数的大小（共1小题）
1．（2022•钢城区）写出一个比大且比小的整数 　 　．
二．因式分解-运用公式法（共3小题）
2．（2023•济南）因式分解：m2﹣16＝　 　．
3．（2022•钢城区）因式分解：a2+4a+4＝　 　．
4．（2021•济南）因式分解：a2﹣9＝　 　．
三．根的判别式（共1小题）
5．（2023•济南）关于x的一元二次方程x2﹣4x+2a＝0有实数根，则a的值可以是 　 　（写出一个即可）．
四．根与系数的关系（共1小题）
6．（2021•济南）关于x的一元二次方程x2+x﹣a＝0的一个根是2，则另一个根是 　 　．
五．解分式方程（共1小题）
7．（2022•钢城区）代数式与代数式的值相等，则x＝　 　．
六．规律型：点的坐标（共1小题）
8．（2022•钢城区）规定：在平面直角坐标系中，一个点作“0”变换表示将它向右平移一个单位，一个点作“1”变换表示将它绕原点顺时针旋转90°，由数字0和1组成的序列表示一个点按照上面描述依次连续变换．例如：如图，点O（0，0）按序列“011…”作变换，表示点O先向右平移一个单位得到O1（1，0），再将O1（1，0）绕原点顺时针旋转90°得到O2（0，﹣1），再将O2（0，﹣1）绕原点顺时针旋转90°得到O3（﹣1，0）…依次类推．点（0，1）经过“011011011”变换后得到点的坐标为　 　．

七．一次函数的应用（共2小题）
9．（2023•济南）学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示，l1和l2分别表示两人到小亮家的距离s（km）和时间t（h）的关系，则出发 　 　h后两人相遇．

10．（2021•济南）漏刻是我国古代的一种计时工具．据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用．小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h（cm）是时间t（min）的一次函数，如表是小明记录的部分数据，其中有一个h的值记录错误，请排除后利用正确的数据确定当h为8cm时，对应的时间t为 　 　min．
t（min）
…
1
2
3
5
…
h（cm）
…
2.4
2.8
3.4
4
…

八．多边形内角与外角（共1小题）
11．（2021•济南）如图，正方形AMNP的边AM在正五边形ABCDE的边AB上，则∠PAE＝　 　．

九．正多边形和圆（共1小题）
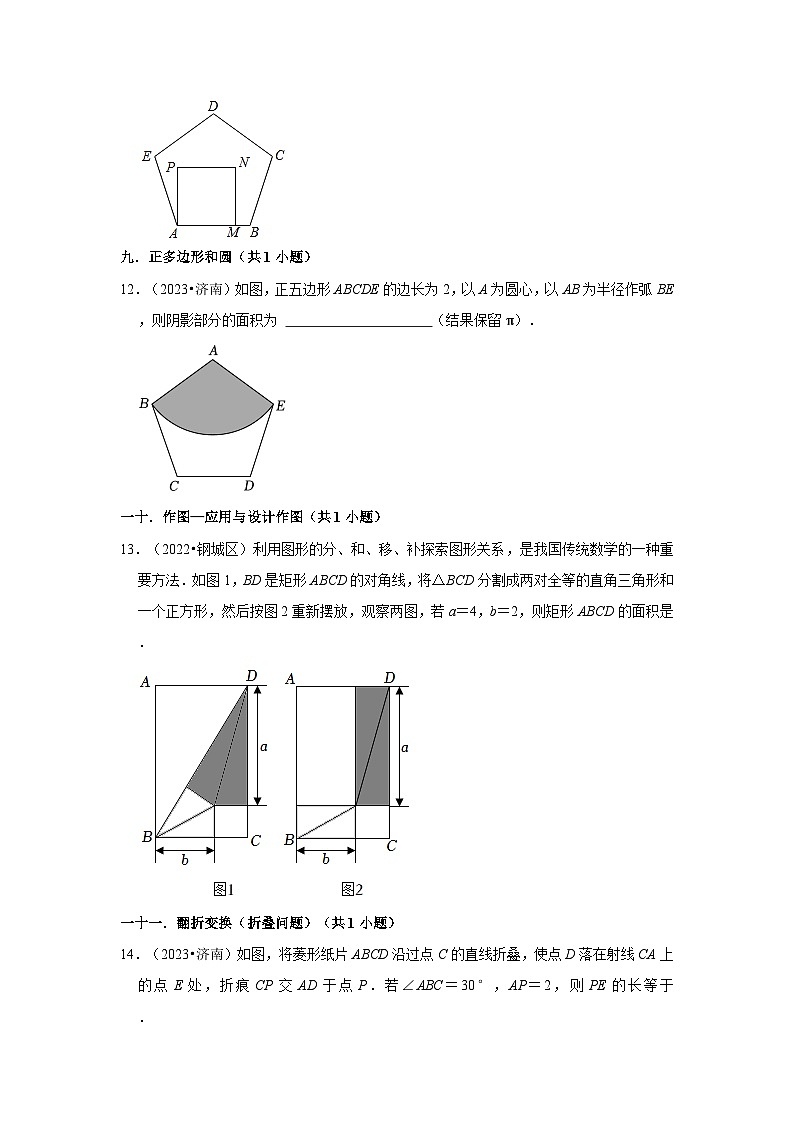
12．（2023•济南）如图，正五边形ABCDE的边长为2，以A为圆心，以AB为半径作弧BE，则阴影部分的面积为 　 　（结果保留π）．

一十．作图—应用与设计作图（共1小题）
13．（2022•钢城区）利用图形的分、和、移、补探索图形关系，是我国传统数学的一种重要方法．如图1，BD是矩形ABCD的对角线，将△BCD分割成两对全等的直角三角形和一个正方形，然后按图2重新摆放，观察两图，若a＝4，b＝2，则矩形ABCD的面积是 　 　．

一十一．翻折变换（折叠问题）（共1小题）
14．（2023•济南）如图，将菱形纸片ABCD沿过点C的直线折叠，使点D落在射线CA上的点E处，折痕CP交AD于点P．若∠ABC＝30°，AP＝2，则PE的长等于 　 　．

一十二．相似三角形的判定与性质（共1小题）
15．（2021•济南）如图，一个由8个正方形组成的“C”模板恰好完全放入一个矩形框内，模板四周的直角顶点M，N，O，P，Q都在矩形ABCD的边上，若8个小正方形的面积均为1，则边AB的长为 　 　．

一十三．概率公式（共1小题）
16．（2023•济南）围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有3个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是，则盒中棋子的总个数是 　 　个．
一十四．几何概率（共2小题）
17．（2022•济南）如果小球在如图所示的地板上自由地滚动，并随机的停留在某块方砖上，那么它最终停留在阴影区域的概率是 　 　．

18．（2021•济南）如图，在两个同心圆中，四条直径把大圆分成八等份，若将飞镖随机投掷到圆面上，则飞镖落在黑色区域的概率是 　 　．


山东省济南市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一．估算无理数的大小（共1小题）
1．（2022•钢城区）写出一个比大且比小的整数 　3（答案不唯一）　．
【答案】3（答案不唯一）..
【解答】解：∵＜2＜3＜4＜，
∴写出一个比大且比小的整数如3（答案不唯一）；
故答案为：3（答案不唯一）．
二．因式分解-运用公式法（共3小题）
2．（2023•济南）因式分解：m2﹣16＝　（m+4）（m﹣4）　．
【答案】（m+4）（m﹣4）．
【解答】解：根据平方差公式：m2﹣16＝（m+4）（m﹣4），
故答案为：（m+4）（m﹣4）．
3．（2022•钢城区）因式分解：a2+4a+4＝　（a+2）2　．
【答案】见试题解答内容
【解答】解：原式＝（a+2）2，
故答案为：（a+2）2．
4．（2021•济南）因式分解：a2﹣9＝　（a+3）（a﹣3）　．
【答案】见试题解答内容
【解答】解：a2﹣9＝（a+3）（a﹣3）．
三．根的判别式（共1小题）
5．（2023•济南）关于x的一元二次方程x2﹣4x+2a＝0有实数根，则a的值可以是 　1　（写出一个即可）．
【答案】1．
【解答】解：∵关于x的一元二次方程x2﹣4x+2a＝0有实数根，
∴Δ＝16﹣8a≥0，
解得：a≤2，
则a的值可以是1．
故答案为：1．
四．根与系数的关系（共1小题）
6．（2021•济南）关于x的一元二次方程x2+x﹣a＝0的一个根是2，则另一个根是 　﹣3　．
【答案】﹣3．
【解答】解：设另一个根为m，由根与系数之间的关系得，
m+2＝﹣1，
∴m＝﹣3，
故答案为﹣3，
五．解分式方程（共1小题）
7．（2022•钢城区）代数式与代数式的值相等，则x＝　7　．
【答案】7．
【解答】解：由题意得，
＝，
去分母得，3（x﹣1）＝2（x+2），
去括号得，3x﹣3＝2x+4，
移项得，3x﹣2x＝4+3，
解得x＝7，
经检验x＝7是原方程的解，
所以原方程的解为x＝7，
故答案为：7．
六．规律型：点的坐标（共1小题）
8．（2022•钢城区）规定：在平面直角坐标系中，一个点作“0”变换表示将它向右平移一个单位，一个点作“1”变换表示将它绕原点顺时针旋转90°，由数字0和1组成的序列表示一个点按照上面描述依次连续变换．例如：如图，点O（0，0）按序列“011…”作变换，表示点O先向右平移一个单位得到O1（1，0），再将O1（1，0）绕原点顺时针旋转90°得到O2（0，﹣1），再将O2（0，﹣1）绕原点顺时针旋转90°得到O3（﹣1，0）…依次类推．点（0，1）经过“011011011”变换后得到点的坐标为　（﹣1，﹣1）　．

【答案】（﹣1，﹣1）．
【解答】解：将点（0，1）经过一次011变换，
即先向右平移一个单位得到（1，1），
再绕点O顺时针旋转90得到（1，﹣1），
再绕点O顺时针旋转90得到（﹣1，﹣1）；
如此将点（﹣1，﹣1）经过011变换得到点（0，1），
再将点（0，1）经过011变换得到点（﹣1，﹣1）．
故答案为：（﹣1，﹣1）．

七．一次函数的应用（共2小题）
9．（2023•济南）学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示，l1和l2分别表示两人到小亮家的距离s（km）和时间t（h）的关系，则出发 　0.35　h后两人相遇．

【答案】0.35．
【解答】解：设l1的函数解析式为y1＝kx+b，
则，
解得，
∴l1的函数解析式为S1＝5t+3.5；
设l2的函数解析式为S2＝mt，
则0.4m＝6，
解得m＝15，
∴l2的函数解析式为S2＝15t；
令S1＝S2，即5t+3.5＝15t，
解得t＝0.35，
∴出发0.35小时后两人相遇．
故答案为：0.35．
10．（2021•济南）漏刻是我国古代的一种计时工具．据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用．小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h（cm）是时间t（min）的一次函数，如表是小明记录的部分数据，其中有一个h的值记录错误，请排除后利用正确的数据确定当h为8cm时，对应的时间t为 　15　min．
t（min）
…
1
2
3
5
…
h（cm）
…
2.4
2.8
3.4
4
…

【答案】15．
【解答】解：设一次函数的表达式为h＝kt+b，t每增加一个单位h增加或减少k个单位，
∴由表可知，当t＝3时，h的值记录错误．
将（1，2.4）（2，2.8）代入得，，
解得k＝0.4，b＝2，
∴h＝0.4t+2，
将h＝8代入得，t＝15．
故答案为：15．
八．多边形内角与外角（共1小题）
11．（2021•济南）如图，正方形AMNP的边AM在正五边形ABCDE的边AB上，则∠PAE＝　18°　．

【答案】18°．
【解答】解：∵五边形ABCDE为正五边形，
∴∠EAB＝＝108°，
∵四边形AMNP为正方形，
∴∠PAM＝90°，
∴∠PAE＝∠EAB﹣∠PAM＝108°﹣90°＝18°．
故答案为：18°．
九．正多边形和圆（共1小题）
12．（2023•济南）如图，正五边形ABCDE的边长为2，以A为圆心，以AB为半径作弧BE，则阴影部分的面积为 　　（结果保留π）．

【答案】．
【解答】解：∠BAE＝＝108°，
∴阴影部分的面积为＝，
故答案为：．
一十．作图—应用与设计作图（共1小题）
13．（2022•钢城区）利用图形的分、和、移、补探索图形关系，是我国传统数学的一种重要方法．如图1，BD是矩形ABCD的对角线，将△BCD分割成两对全等的直角三角形和一个正方形，然后按图2重新摆放，观察两图，若a＝4，b＝2，则矩形ABCD的面积是 　16　．

【答案】16．
【解答】解：设小正方形的边长为x，
∵a＝4，b＝2，
∴BD＝2+4＝6，
在Rt△BCD中，DC2+BC2＝DB2，
即（4+x）2+（x+2）2＝62，
整理得，x2+6x﹣8＝0，
而长方形面积为＝（x+4）（x+2）＝x2+6x+8＝8+8＝16
∴该矩形的面积为16，
解法二：由题意得第一个矩形的左上角的三角形面积＝第二个矩形左上角的长方形的面积＝4×2＝8，所以原矩形面积为16
故答案为：16．

一十一．翻折变换（折叠问题）（共1小题）
14．（2023•济南）如图，将菱形纸片ABCD沿过点C的直线折叠，使点D落在射线CA上的点E处，折痕CP交AD于点P．若∠ABC＝30°，AP＝2，则PE的长等于 　+　．

【答案】+．
【解答】解：过点A作AF⊥PE于点F，
∵四边形ABCD是菱形，
∴∠D＝∠ABC＝30°，AD＝CD，
∴∠DAC＝＝75°，
由折叠可知：∠E＝∠D＝30°，
∴∠APE＝∠DAC﹣∠AEP＝45°，
在Rt△APF中，PF＝AP•cos∠APE，
∴PF＝AF＝2×cos45°＝，
在Rt△AEF中，tan∠AEP＝，
∴EF＝＝＝，
∴PE＝PF+EF＝+，
故答案为：+．

一十二．相似三角形的判定与性质（共1小题）
15．（2021•济南）如图，一个由8个正方形组成的“C”模板恰好完全放入一个矩形框内，模板四周的直角顶点M，N，O，P，Q都在矩形ABCD的边上，若8个小正方形的面积均为1，则边AB的长为 　　．

【答案】．
【解答】解：如图所示，连接EG，则∠OEP＝90°，

由题意得，小正方形的边长为1，
∴OP＝＝＝，
∵四边形ABCD是矩形，
∴∠B＝∠C＝∠A＝90°，∠MQP＝90°，
∴∠BMQ＝∠CQP＝90°﹣∠MQP，
同理∠EPO＝∠CQP＝90°﹣∠QPC，
∴∠BMQ＝∠EPO，
又∠OEP＝∠B＝90°，
∴△OEP∽△QBM，
∴＝＝＝，
∴BM＝＝＝，QB＝＝＝，
∵∠B＝∠A＝90°，∠NMQ＝90°，
∴∠BMQ＝∠ANM＝90°﹣∠AMN，
在△QBM和△MAN中，
，
∴△QBM≌△MAN（AAS），
∴AM＝QB＝，
∴AB＝BM+AM＝+＝．
故答案为：．
一十三．概率公式（共1小题）
16．（2023•济南）围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有3个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑色棋子的概率是，则盒中棋子的总个数是 　12　个．
【答案】见试题解答内容
【解答】解：由题意：3÷＝12（个），
故答案为：12．
一十四．几何概率（共2小题）
17．（2022•济南）如果小球在如图所示的地板上自由地滚动，并随机的停留在某块方砖上，那么它最终停留在阴影区域的概率是 　　．

【答案】．
【解答】解：∵总面积为9个小正方形的面积，其中阴影部分面积为4个小正方形的面积，
∴小球停在阴影部分的概率是，
故答案为：．
18．（2021•济南）如图，在两个同心圆中，四条直径把大圆分成八等份，若将飞镖随机投掷到圆面上，则飞镖落在黑色区域的概率是 　　．

【答案】见试题解答内容
【解答】解：因为两个同心圆等分成八等份，飞镖落在每一个区域的机会是均等的，其中黑色区域的面积占了其中的四等份，
所以P（飞镖落在黑色区域）＝＝．
故答案为：．