2024年高考物理复习第一轮：创新实验课(06)　探究向心力大小与半径、角速度、质量的关系

实验基础知识

一、实验基本技能

1．实验目的

(1)学会使用向心力演示器．

(2)探究向心力大小与半径、角速度、质量的关系．

2．实验原理

(1)探究方法：控制变量法．

(2)定性感知实验设计思路

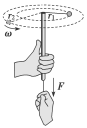
如图所示，细线穿在圆珠笔的杆中，一端拴住小球，另一端用一只手牵住，另一只手抓住圆珠笔杆并用力转动，使小球做圆周运动，可近似地认为作用在小球上的细线的拉力提供了小球做圆周运动所需的向心力，而细线的拉力可用牵住细线的手的感觉来判断．

(3)定量分析实验设计思路

①控制小球质量和运动半径不变，探究向心力大小与角速度的关系．

②控制小球质量和角速度不变，探究向心力大小与运动半径的关系．

③控制小球运动半径和角速度不变，探究向心力大小与质量的关系．

匀速转动手柄，可以使塔轮、长槽和短槽匀速转动，槽内的小球也就随之做匀速圆周运动．这时，小球向外挤压挡板，挡板对小球的反作用力提供了小球做匀速圆周运动的向心力．同时，小球压挡板的力使挡板另一端压缩弹簧测力套筒里的弹簧，弹簧的压缩量可以从标尺上读出，该读数显示了向心力大小．

3．实验器材：质量不同的小球若干，空心圆珠笔杆，细线(长约60 cm)，向心力演示器．

4．实验步骤

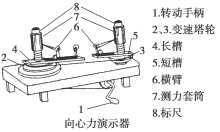
(1)向心力大小与哪些因素有关的定性感知．

①在小物体的质量和角速度不变的条件下，改变小物体做圆周运动的半径进行实验．

②在小物体的质量和做圆周运动的半径不变的条件下，改变物体的角速度进行实验．

③换用不同质量的小物体，在角速度和半径不变的条件下，重复上述操作．

(2)向心力与质量、角速度、半径关系的定量分析．

匀速转动手柄，可以使塔轮、长槽和短槽匀速转动，槽内的小球也就随之做匀速圆周运动．这时，小球向外挤压挡板，挡板对小球的反作用力提供了小球做匀速圆周运动的向心力．同时，小球压挡板的力使挡板另一端压缩弹簧力套筒里的弹簧，弹簧的压缩量可以从标尺上读出，该读数显示了向心力大小．

①把两个质量相同的小球放在长槽和短槽上，使它们的转动半径相同．调整塔轮上的皮带，使两个小球的角速度不一样．注意向心力的大小与角速度的关系．

②保持两个小球质量不变，增大长槽上小球的转动半径．调整塔轮上的皮带，使两个小球的角速度相同．注意向心力的大小与半径的关系．

③换成质量不同的球，分别使两球的转动半径相同．调整塔轮上的皮带，使两个小球的角速度也相同．注意向心力的大小与质量的关系．

④重复几次以上实验．

二、规律方法总结

1．数据处理

(1)把两个质量相同的小球放在长槽和短槽上，使它们的转动半径相同，调整塔轮上的皮带，使两个小球转动的角速度之比分别为1∶1、1∶2和1∶3，分别读出两球所需的向心力大小，将结果填入表一．

表一：m1＝m2，r1＝r2.

(2)把两个质量相同的小球放在长槽和短槽上，使半径之比为2∶1；调整塔轮上的皮带，使两个小球的角速度相同，分别读出两球所需的向心力大小，将结果填入表二．

表二：m1＝m2，ω1＝ω2.

(3)把两个质量不同的小球放在长槽和短槽上，使两球的转动半径相同，调整塔轮上的皮带，使两个小球的角速度相同，分别读出两球所需的向心力大小，将结果填入表三．

表三：r1＝r2，ω1＝ω2.

(4)分别作出F向­ω2、F向­r.F向­m的图像．

2．实验结论

物体做圆周运动需要的向心力跟物体的质量成正比，跟半径成正比，跟角速度的平方成正比．

3．注意事项

(1)定性感知实验中，轻小物体受到的重力与拉力相比可忽略．

(2)使用向心力演示器时应注意：

①将横臂紧固螺钉旋紧，以防小球和其他部件飞出而造成事故．

②摇动手柄时应力求缓慢加速，注意观察其中一个测力计的格数．达到预定格数时，即保持转速均匀恒定．

命题点一　实验原理与操作

　用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关．

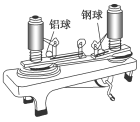
(1)本实验采用的科学方法是________．

A．控制变量法　　　　　　 B．累积法

C．微元法  D．放大法

(2)图示情景正在探究的是________．

A．向心力的大小与半径的关系

B．向心力的大小与线速度大小的关系

C．向心力的大小与角速度大小的关系

D．向心力的大小与物体质量的关系

(3)通过本实验可以得到的结论是________．

A．在质量和半径一定的情况下，向心力的大小与角速度成正比

B．在质量和半径一定的情况下，向心力的大小与线速度的大小成正比

C．在半径和角速度一定的情况下，向心力的大小与质量成正比

D．在质量和角速度一定的情况下，向心力的大小与半径成反比

解析：(1)探究向心力大小与半径、角速度、质量的关系，要采用控制变量法探究，故正确选项为A．

(2)实验中，两小球的种类不同，故是保持两小球的转动半径、转动的角速度相同，探究向心力的大小跟物体质量的定量关系．故正确选项为D．

(3)两小球的转动半径、转动的角速度相同，探究向心力的大小跟物体质量成正比．故正确选项为C．

答案：(1)A　(2)D　(3)C

[对点演练]

1.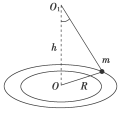某同学用圆锥摆验证向心力公式F＝mRω2.先在一张白纸上以O为圆心画一组同心圆，再将白纸铺在水平桌面上，在O点正上方距桌面高为h处的O1处用铁架台(图中未画出)悬挂一质量为m的小球，设法使小球沿着半径为R的圆周运动但恰不与纸面接触．

(1)现用刻度尺测得R、h，用天平测得m，用g表示重力加速度，则小球所受的合力F1＝______．

(2)为了测出小球做圆周运动的角速度ω，先用停表测得小球完成n次圆周运动共用时t，则由向心力公式F＝mRω2求得小球做圆周运动的向心力F2＝________，代入数值，验证F1＝F2是否成立．

解析：(1)设摆线与竖直方向的夹角为α，则有tan α＝，

小球做圆周运动中所受合力的表达式为F1＝mgtan α＝.

(2)小球做圆周运动的周期为T＝，向心加速度的表达式为an＝＝，

小球做圆周运动的向心力F2＝man＝m，

所以若能大致满足F1＝F2，就可达到粗略验证向心力表达式的目的．

答案：(1)　(2)m

命题点二　数据处理与误差分析

　某同学利用如图所示的向心力演示器定量探究匀速圆周运动所需向心力F跟小球质量m、转速n和运动半径r之间的关系．

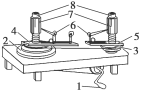
(1)为了单独探究向心力跟小球质量的关系，必须用________法．

(2)转动手柄可以使长槽和短槽分别随变速塔轮匀速转动，槽内的球随之做匀速圆周运动．这时我们可以看到弹簧测力筒上露出标尺，通过标尺上红白相间等分格数，即可求得两个球所受的___________________________________________________________．

(3)该同学通过实验得到如下表的数据：

根据以上数据，可归纳概括出向心力F跟小球质量m、转速n和运动半径r之间的关系是：________________________________________________(文字表述)．

(4)实验中遇到的问题有：_________________________(写出一点即可)．

解析：(1)为了单独探究向心力跟小球质量的关系，需要控制转速n和运动半径r不变，所以需要采用控制变量法．

(2)标尺上红白相间等分格子的多少可以显示小球所受向心力的大小，所以通过标尺上红白相间等分格数，即可求得两个球所受的向心力大小之比．

(3)根据表格中数据可知向心力F跟小球质量m成正比，跟转速n的平方成正比，跟运动半径r成正比(或向心力F跟小球质量m、转速n的平方、运动半径r的乘积成正比)．

(4)实验中可能遇到的问题是难以保证小球做匀速圆周运动，转速难按比例调节和露出格子数(或力的读数)不稳定，难定量化．

答案：(1)控制变量　(2)向心力大小之比(或向心力之比)

(3)向心力F跟小球质量m成正比，跟转速n的平方成正比，跟运动半径r成正比(或向心力F跟小球质量m、转速n的平方、运动半径r的乘积成正比)

(4)难以保证小球做匀速圆周运动，转速难按比例调节和露出格子数(或力的读数)不稳定，难定量化

[对点演练]

2．如图所示，图甲为“用向心力演示器验证向心力公式”的实验示意图，图乙为俯视图．图中A、B槽分别与a、b轮同轴固定，且a、b轮半径相同．当a、b两轮在皮带的带动下匀速转动．

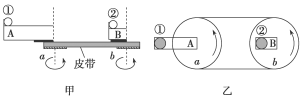
(1)两槽转动的角速度ωA________ωB．(选填“>”“＝”或“<”) .

(2)现有两质量相同的钢球，①球放在A槽的边缘，②球放在B槽的边缘，它们到各自转轴的距离之比为2∶1.则钢球①、②的线速度之比为________；受到的向心力之比为________．

解析：(1)因a、b两轮转动的角速度相同，而两槽的角速度与两轮的角速度相同，则两槽转动的角速度相等，即ωA＝ωB．

(2)钢球①、②的角速度相同，半径之比为2∶1，则根据v＝ωr可知，线速度之比为2∶1；根据F＝mω2r可知，受到的向心力之比为2∶1.

答案：(1)＝　(2)2∶1　2∶1

命题点三　创新拓展实验

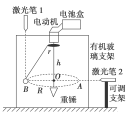
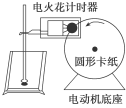
　如图所示为改装的探究圆周运动的向心加速度的实验装置．有机玻璃支架上固定一个直流电动机，电动机转轴上固定一个半径为r的塑料圆盘，圆盘中心正下方用细线接一个重锤，圆盘边缘连接细绳，细绳另一端连接一个小球．实验操作如下：

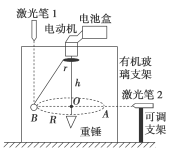
①利用天平测量小球的质量m，记录当地的重力加速度g的大小；

②闭合电源开关，让小球做如图所示的匀速圆周运动，调节激光笔2的高度和激光笔1的位置，让激光恰好照射到小球的中心，用刻度尺测量小球做圆周运动的半径R和球心到塑料圆盘的高度h；

③当小球第一次到达A点时开始计时，并记录为1次，记录小球n次到达A点的时间t；

④切断电源，整理器材．

请回答下列问题：

(1)(多选)下列说法正确的是________．

A．小球运动的周期为

B．小球运动的线速度大小为

C．小球运动的向心力大小为

D．若电动机转速增加，激光笔1、2应分别左移、升高

(2)若已测出R＝40.00 cm、r＝4.00 cm，h＝90.00 cm，t＝100.00 s，n＝51，π取3.14，则小球做圆周运动的周期T＝________s，记录的当地重力加速度大小应为g＝________m/s2.(计算结果均保留三位有效数字)

解析：(1)从球第1次到第n次通过A位置，转动圈数为n－1，时间为t，故周期为T＝，故A错误；小球的线速度大小为v＝＝，故B正确；小球受重力和拉力，合力提供向心力，设线与竖直方向的夹角为α，则Tcos α＝mg，Tsin α＝F向，故F向＝mgtan α＝mg，故C错误；若电动机的转速增加，则转动半径增加，故激光笔1、2应分别左移、上移，故D正确．

(2)小球做圆周运动的周期T＝＝ s＝2.00 s；

向心力F向＝mg＝mR，解得g＝＝9.86 m/s2.

答案：(1)BD　(2)2.00　9.86

[对点演练]

3．(实验器材的创新)利用如图实验装置可验证做匀速圆周运动的物体所受合力与所需向心力的“供”“需”关系，启动小电动机带动小球做圆锥摆运动，不计一切阻力，移动水平圆盘，当盘与球恰好相切时关闭电动机，让球停止运动，悬线处于伸直状态．利用弹簧测力计水平径向向外拉小球，使小球恰好离开圆盘且处于静止状态时，测出水平弹力的大小F.

(1)(多选)为算出小球做匀速圆周运动时所需向心力，下列物理量还应该测出的有________；

A．用秒表测出小球运动周期T

B．用刻度尺测出小球做匀速圆周运动半径r

C．用刻度尺测出小球到线的悬点的竖直高度h

D．用天平测出小球质量m

(2)小球做匀速圆周运动时，所受重力与线拉力的合力大小________弹簧测力计测出F大小；(选填“大于”“等于”或“小于”)

(3)当所测物理量满足________关系式时，则做匀速圆周运动的物体所受合力与所需向心力的“供”“需”平衡．

解析：(1)根据向心力公式Fn＝mr分析知，为算出小球做匀速圆周运动时所需向心力，需要测出小球做匀速圆周运动的周期T、半径r和小球质量m，故A、B、D正确，C错误．

(2)据题意，小球静止时，F等于悬线拉力的水平分力，即有F＝mgtan θ，θ是悬线与竖直方向的夹角，小球做匀速圆周运动时，由重力与悬线拉力的合力提供向心力，重力与悬线拉力的合力大小F合＝mgtan θ，则F合＝F.

(3)当F合＝Fn，即F＝mr时，做匀速圆周运动的物体所受合力与所需向心力的“供”“需”平衡．

答案：(1)ABD　(2)等于　(3)F＝mr

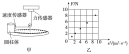
4．(数据处理的创新)如图甲所示是某同学探究做圆周运动的物体质量、向心力、轨道半径及线速度关系的实验装置，圆柱体放置在水平光滑圆盘上做匀速圆周运动．力传感器测量向心力F，速度传感器测量圆柱体的线速度v，该同学通过保持圆柱体质量和运动半径不变，来探究向心力F与线速度v的关系．

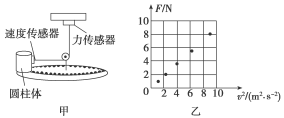
(1)该同学采用的实验方法为________．

A．等效替代法　   B．控制变量法　　 C．理想化模型法

(2)改变线速度v，多次测量，该同学测出了五组F、v数据，如下表所示：

该同学对数据分析后，在图乙坐标纸上描出了五个点．

①作出F­v2图线；

②若圆柱体运动半径r＝0.2 m，由作出的F­v2的图线可得圆柱体的质量m＝________kg.(结果保留两位有效数字)

解析：(1)实验中研究向心力和线速度的关系，保持圆柱体质量和运动半径不变，采用的实验方法是控制变量法，故选B．

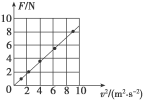
(2)①作出F­v2图线，如图所示．

②根据F＝m，图线的斜率k＝，代入数据解得m＝0.18 kg.

答案：(1)B　(2)①见解析图　②0.18