
2023年广西南宁市兴宁区新民中学中考数学模拟试卷(含解析)
展开2023年广西南宁市兴宁区新民中学中考数学模拟试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. −2的倒数是( )
A. −2 B. −12 C. 12 D. 2
2. C919飞机是中国按照国际民航规章自行研制、具有自主知识产权的大型喷气式民用飞机,最大飞行高度约为12100米,标志着我国大飞机事业迈入规模化系列化发展新征程.数据“12100”用科学记数法表示为( )
A. 1.21×103 B. 1.21×104 C. 12.1×103 D. 0.121×105
3. 某物体的三视图如图所示,那么该物体形状可能是( )
A. 圆柱
B. 球
C. 圆锥
D. 长方体
4. 下列式子中,最简二次根式的是( )
A. 8 B. 7 C. 12 D. 13
5. 在平面直角坐标系中,点P(3,−2)关于x轴的对称点的坐标是( )
A. (−3,−2) B. (−3,2) C. (3,2) D. (−2,3)
6. 如图是甲、乙两名射击运动员10次射击成绩的折线统计图,记甲10次成绩的方差为S甲2,乙10次成绩的方差为S乙2,根据折线图判断下列结论中正确的是( )
A. S甲2>S乙2 B. S甲2
A. 25° B. 50° C. 130° D. 155°
8. 已知2x+y=5x+2y=6,那么x−y的值是( )
A. 1 B. −1 C. 0 D. 2
9. 抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )
A. 16 B. 13 C. 12 D. 23
10. 在“双减政策”的推动下,我县某中学学生每天书面作业时长明显减少.2022年上学期每天书面作业平均时长为100min,经过2022年下学期和2023年上学期两次调整后,2023年上学期平均每天书面作业时长为70min.设该校这两学期平均每天作业时长每期的下降率为x,则可列方程为( )
A. 70(1+x2)=100 B. 70(1+x)2=100
C. 100(1−x)2=70 D. 100(1−x2)=70
11. 将图(甲)中阴影部分的小长方形变换到图(乙)位置,根据两个图形的面积关系得到的数学公式是( )
A. (a+b)2=a2+2ab+b2 B. (a−b)2=a2−2ab+b2
C. a2−b2=(a+b)(a−b) D. (a+2b)(a−b)=a2+ab−2b2
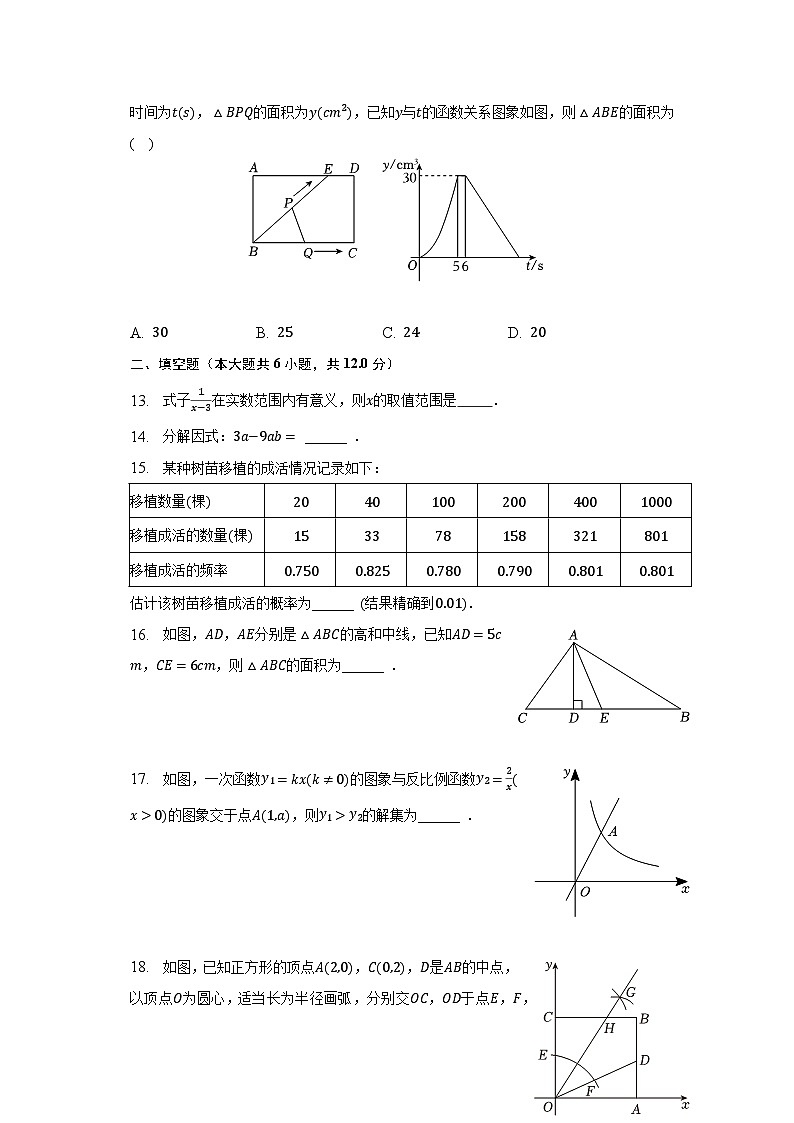
12. 如图,E为矩形ABCD边AD上的一点,点P从点B沿折线BE−ED−DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是2cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系图象如图,则△ABE的面积为( )
A. 30 B. 25 C. 24 D. 20
二、填空题(本大题共6小题,共12.0分)
13. 式子1x−3在实数范围内有意义,则x的取值范围是 .
14. 分解因式:3a−9ab= ______ .
15. 某种树苗移植的成活情况记录如下:
移植数量(棵)
20
40
100
200
400
1000
移植成活的数量(棵)
15
33
78
158
321
801
移植成活的频率
0.750
0.825
0.780
0.790
0.801
0.801
估计该树苗移植成活的概率为______ (结果精确到0.01).
16. 如图,AD,AE分别是△ABC的高和中线,已知AD=5cm,CE=6cm,则△ABC的面积为______ .
17. 如图,一次函数y1=kx(k≠0)的图象与反比例函数y2=2x(x>0)的图象交于点A(1,a),则y1>y2的解集为______ .
18. 如图,已知正方形的顶点A(2,0),C(0,2),D是AB的中点,以顶点O为圆心,适当长为半径画弧,分别交OC,OD于点E,F,再分别以点E,F为圆心,大于12EF的长为半径画弧,两弧交于点G,作射线OG交边BC于点H,则点H的坐标为______ .
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题6.0分)
计算:−22+ 8−3+13.
20. (本小题6.0分)
解不等式组:3x−5≤x+1,①x−12>x−4.②
21. (本小题10.0分)
如图,在正方形网格中,每个小正方形的边长均为1个单位长度,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(−1,2),B(−3,1),C(0,−1).
(1)将△ABC向右平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C按逆时针方向旋转90°后得到△A2B2C2,画出△A2B2C2;
(3)在(2)的条件下,求边AC扫过的面积.
22. (本小题10.0分)
某校为加强学生的消防意识,开展了“消防安全知识“宣传活动,并分别在七、八年级中各随机抽取10名学生的消防知识成绩进行了统计,整理与分析(成绩用x表示,共分为三个等级:合格80≤x<85,良好85≤x<95,优秀x≥95),下面给出了部分信息:
10名七年级学生的成绩:83,84,84,88,89,89,95,95,95,98
10名八年级学生中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的八年级10名学生的成绩扇形统计图
抽取的七、八年级学生成绩统计表
年级
平均数
中位数
众数
“优秀”“等级所占百分比
七年级
90
89
a
40%
八年级
90
b
90
30%
(1)八年级10名学生中“合格”等级的人数在扇形统计图中所占圆心角的度数为______ 度;
(2)填空:a= ______ ,b= ______ ;
(3)根据以上数据,你认为该校七八年级中,哪个年级学生对消防知识掌握得更好?请说明理由,并对如何加强学生的消防意识写出一条你的看法.
23. (本小题10.0分)
如图,MN是⊙O的直径,A,B是⊙O上的两点,过点A作⊙O的切线交BN的延长线于点C,BC⊥AC,连接AB,AM.
(1)求证:∠BNM=2∠AMN;
(2)若tan∠ABC=12,⊙O的半径为 5,求线段AC的长.
24. (本小题10.0分)
如图①,郑北大桥横跨亚洲最大铁路编组站,该桥为独塔双索钢混结合梁斜拉桥,是国内同类型桥中最宽的结合梁斜拉桥.某数学“综合与实践”小组的同学把“测量郑北大桥的某组斜拉索最高点到桥面的距离”作为一项课题活动,进行了探究,具体过程如下:
方案设计:如图②,分别在A,B两点放置测角仪测得∠CDE和∠CED的度数;
数据收集:A,B两点的距离为260米,测角仪AD和BE的高度为1.5米,∠CDE=53°,∠CED=45°;
问题解决:求郑北大桥某组斜拉索最高点C到桥面AB的距离.(结果保留整数.参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
(1)根据上述方案及数据,请你完成求解过程;
(2)你认为在本次方案的实行过程中,该小组成员应该注意的事项有哪些(写出一条即可).
25. (本小题10.0分)
【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:△ABC∽△ACD.
【尝试应用】(2)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A,若BF=4,BE=3,求AD的长.
【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF//AC,AC=2EF,∠EDF=12∠BAD,AE=2,DF=5,求菱形ABCD的边长.
26. (本小题10.0分)
如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(−1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度;
(3)当a−1≤x≤a时,二次函数y=x2+bx+c的最小值为2a,求a的值.
答案和解析
1.【答案】B
【解析】解:因为−2×(−12)=1.
所以−2的倒数是−12,
故选:B.
根据倒数的定义,乘积是1的两个数互为倒数解答即可.
本题主要考查倒数的定义,解决本题的关键是熟记乘积是1的两个数互为倒数.
2.【答案】B
【解析】解:12100=1.21×104.
故选:B.
用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.【答案】C
【解析】解:A.圆柱的三视图无三角形,故A不符合;
B.球的三视图无三角形,故B不符合;
C.圆锥的主视图和左视图都是三角形,俯视图是带圆心的圆,故C符合;
D.长方体的三视图无圆和三角形,故D不符合.
故选:C.
根据三视图直接判断圆锥即可.
本题主要考查三视图,解题关键是空间想象能力.
4.【答案】B
【解析】解:A、 8=2 2,故不是最简二次根式,不合题意;
B、 7,是最简二次根式,符合题意;
C、 12=2 3,故不是最简二次根式,不合题意;
D、 13= 33,故不是最简二次根式,不合题意.
故选:B.
直接利用最简二次根式的定义分析得出答案.
此题主要考查了最简二次根式,正确把握相关定义是解题关键.
5.【答案】C
【解析】解:点P(3,−2)关于x轴的对称点的坐标为(3,2).
故选:C.
直接利用关于x轴对称点的性质:横坐标不变,纵坐标互为相反数分析得出答案.
此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的符号是解题关键.
6.【答案】A
【解析】解:由折线统计图得乙运动员的成绩波动较大,所以S甲2>S乙2.
故选:A.
利用折线统计图可判断乙运动员的成绩波动较大,然后根据方差的意义可得到甲乙的方差的大小.
本题考查了折线统计图和方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
7.【答案】B
【解析】解:∵AC=AC,∠AOD=25°,
∴∠AOD=2∠ACD=50°,
故选:B.
利用圆周角的定理即可求得答案.
本题考查圆周角定理,此为基础且重要知识点,必须熟练掌握.
8.【答案】B
【解析】
【分析】
此题主要考查了二元一次方程组的解,关键是注意观察,找出解决问题的简便方法.解题时要根据方程组的特点进行有针对性的计算,注意整体思想的渗透.
直接将二元一次方程组的方程①−②,即可求得x−y的值.
【解答】
解:方程组2x+y=5 ①x+2y=6 ②,
①−②得:x−y=−1.
故选B.
9.【答案】B
【解析】解:∵抛掷六个面上分别刻有的1,2,3,4,5,6的骰子有6种结果,其中朝上一面的数字小于3的有2种,
∴朝上一面的数字小于3的倍数概率是26=13.
故选:B.
用朝上的数字小于3的情况数除以总情况数即为所求的概率.
本题考查了概率公式的应用,掌握概率等于所求情况数与总情况数之比是关键.
10.【答案】C
【解析】解:设根据题意得:100(1−x)2=70.
故选:C.
利用2023年上学期平均每天书面作业时长=2022年上学期每天书面作业平均时长×(1−该校这两学期平均每天作业时长每期的下降率)2,即可列出关于x的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
11.【答案】C
【解析】解:甲图形的面积为a2−b2,乙图形的面积为(a+b)(a−b),
根据两个图形的面积相等知,a2−b2=(a+b)(a−b),
故选:C.
首先求出甲的面积为a2−b2,然后求出乙图形的面积为(a+b)(a−b),根据两个图形的面积相等即可判定是哪个数学公式.
本题主要考查平方差的几何背景的知识点,求出两个图形的面积相等是解答本题的关键.
12.【答案】C
【解析】解:由图象可知,
BC=BE=5×2=10(cm),ED=2×(6−5)=2(cm),
∴AE=AD−ED=BC−ED=10−2=8(cm),
当t=5时,y=S△BPQ=S△BEC=12BC⋅CD=12×10⋅CD=30,
∴CD=6=AB,
∴S△ABE=12AE⋅AB=12×8×6=24(cm2),
故选:C.
根据图象可以得到BC、ED的长度,再用当t=5时△BPQ的面积为30求出CD的长,再用三角形的面积公式求出△ABE的面积.
本题考查动点问题的函数图象,解题的关键是明确题意,利用数形结合的思想,找出所求问题需要的条件.
13.【答案】x≠3
【解析】
【分析】
本题主要考查了分式有意义的条件.注意:“分母不为零”这个条件不能少.
分式有意义的条件为:分母≠0,列出不等式计算即可.
【解答】
解:根据分式有意义的条件得:x−3≠0,
∴x≠3,
故答案为:x≠3.
14.【答案】3a(1−3b)
【解析】解:原式=3a(1−3b).
故答案为:3a(1−3b).
利用提公因式法因式分解.
本题考查因式分解−提公因式法,解题的关键是掌握提公因式的方法.
15.【答案】0.80
【解析】解:由表知,估计该树苗移植成活的概率为0.80,
故答案为:0.80.
利用频率估计概率求解即可.
本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
16.【答案】30cm2
【解析】解:∵AE是△ABC的中线,CE=6cm,
∴BC=2CE=12cm,
∵AD是△ABC的高,
∴S△ABC=12AD⋅BC=30cm2,
故答案为:30cm2.
先根据中线的定义求出BC=2CE=12cm,再根据三角形面积公式求解即可.
本题主要考查了求三角形面积,熟知三角形高和中线的定义是解题的关键.
17.【答案】x>1
【解析】解:∵反比例函数 y2=2x(x>0) 的图象经过点A(1,a),
∴1×a=2,即a=2,
∴A(1,2),
又∵一次函数 y1=kx(k≠0)的图象经过点A(1,2),
∴1×k=2,即k=2,
∴一次函数解析式为:y1=2x,
由图可得:当y1>y2 时,一次函数图象在反比例函数图象的上方,
∴x>1,
故答案为:x>1.
先把点A的坐标代入反比函数解析式求得a=2,再把点A的坐标代入一次函数解析式求得k=2,再结合图形可得当y1>y2 时,一次函数图象在反比例函数图象的上方,即可得出结果.
本题考查反比例函数与一次函数的交点问题、一次函数与反比例函数交点求不等式的解集,运用数形结合的思想是解题的关键.
18.【答案】( 5−1,2)
【解析】解:∵四边形OABC为正方形,A(2,0),C(0,2),
∴OC=OA=AB=BC=2,∠OAD=∠ABC=∠OCB=90°,OC//AB,
∵D点为AB的中点,
∴AD=BD=1,
在Rt△OAD中,OD= 12+22= 5,
延长AB交OG于M点,如图,由作法得OG平分∠COD,
∴∠COM=∠DOM,
∵OC//AM,
∴∠COM=∠AMO,
∴∠AMO=∠DOM,
∴DM=DO= 5,
∴BM= 5−1,
∵BM//OC,
∴CHBH=OCBM=2 5−1,
设CH=2x,则BH=( 5−1)x,
∴2x+( 5−1)x=2,
解得x= 5−12,
∴CH=2x= 5−1,
∴点H的坐标为( 5−1,2).
故答案为:( 5−1,2).
先利用正方形的性质得到OC=OA=AB=BC=2,∠OAD=∠ABC=∠OCB=90°,OC//AB,再利用勾股定理计算出OD= 5,延长AB交OG于M点,如图,利用基本作图得到∠COM=∠DOM,接着证明∠AMO=∠DOM得到DM=DO= 5,然后根据平行线分线段成比例定理得到CHBH=2 5−1,设CH=2x,则BH=( 5−1)x,所以2x+( 5−1)x=2,则解方程求出x得到CH= 5−1,从而得到点H的坐标.
本题考查了作图−基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了正方形的性质和相似三角形的判定与性质.
19.【答案】解:原式=−4+2 2−3+13
=−203+2 2.
【解析】直接利用二次根式的性质以及实数的混合运算法则分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
20.【答案】解:解不等式①,得x<3,
解不等式②,得x<7,
∴不等式组的解集为x<7.
【解析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
21.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)AC= 32+12= 10,
∴边AC扫过的面积=90π×( 10)2360=5π2.
【解析】(1)根据平移变换的性质找出对应点即可求解;
(2)根据旋转变换的性质找出对应点即可求解;
(3)根据扇形的面积公式求解即可.
本题考查了平移变换的性质与旋转变换的性质,熟练掌握平移变换的性质与旋转变换的性质是解题的关键.
22.【答案】72 95 90
【解析】解:(1)八年级10名学生中“合格”等级的人数所占百分比为1−30%−510×100%=20%,
∴八年级10名学生中“合格”等级的人数在扇形统计图中所占圆心角的度数为360°×20%=72°,
故答案为:72;
(2)10名七年级学生的成绩95出现的最多,所以众数为a=95,
∵八年级10名学生的成绩优秀”等级所占百分比为30%,
∴八年级10名学生的成绩优秀”等级的人数为10×30%=3,
∵八年级10名学生的成绩的中位数是第5和第6个数据的平均数,
∴b=12×(90+90)=90,
故答案为:95,90;
(3)该校七、八年级中,七年级学生对消防知识掌握得更好,
理由:虽然七、八年级的平均分均为90分,但七年级的众数高于八年级的众数,所以七年级学生对消防知识掌握得更好;
建议:加强“消防安全知识”的教育.
(1)求出八年级10名学生中“合格”等级的人数所占百分比,乘以360°即可求解;
(2)根据中位数和众数的定义即可得到结论;
(3)根据平均数,众数和方差即可得出结论.
本题考查读扇形统计图的能力和利用统计图获取信息的能力,正确利用统计图获取信息,作出正确的判断和解决问题是解题关键.
23.【答案】解:(1)连接OA,
∴∠AON=2∠AMN,
∵AC是⊙O的切线,BC⊥AC,
∴∠OAC=90°=∠C,
∴∠OAC+∠C=180°,
∴OA//BC,
∴∠BNM=∠AON=2∠AMN.
(2)连接AN,
∵MN是⊙O的直径,
∴∠MAN=90°,
∴∠ABC=∠AMN,
∵⊙O的半径为 5,tan∠ABC=12,
∴tan∠AMN=12,
∴2AN=AM,
在Rt△AMN中,AN2+AM2=MN2,
∴AN=2,
∵ON=OA,
∴∠ONA=∠OAN且∠ONA+∠AMN=∠OAN+∠CAN,
∴∠CAN=∠AMN,故△ANC的三边之比为 5:2:1,
∴AC=2 5×2=4 55.
【解析】(1)连接OA,得∠AON=2∠AMN,再根据题意得OA//BC,即可解答.
(2)连接AN,根据题意得∠ABC=∠AMN,再根据⊙O的半径为 5,tan∠ABC=12,得到AN=2,再根据ON=OA,得△ANC的三边之比为 5:2:1,即可解答.
本题考查了切线的判定定理,垂径定理,掌握垂径定理是解题关键.
24.【答案】解:(1)过点C作CG⊥DE,并延长CG交AB于点H,
由题意得:AD=GH=EB=1.5米,AB=DE=260米,
设DG=x米,
在Rt△CDG中,∠CDG=53°,
∴CG=DG⋅tan53°≈1.33x(米),
在Rt△CGE中,∠CEG=45°,
∴EG=CGtan45∘=1.33x(米),
∵DG+GE=DE,
∴x+1.33x=260,
解得:x≈111.6,
∴CH=CG+GH=1.33x+1.5≈150(米),
∴郑北大桥某组斜拉索最高点C到桥面AB的距离约为150米;
(2)我认为在本次方案的实行过程中,该小组成员应该注意的事项是:使用测角仪测量时,要与地面垂直.
【解析】(1)过点C作CG⊥DE,并延长CG交AB于点H,根据题意可得:AD=GH=EB=1.5米,AB=DE=260米,然后设DG=x米,在Rt△CDG中,利用锐角三角函数的定义求出CG的长,再在Rt△CGE中,利用锐角三角函数的定义求出GE的长,从而根据DG+GE=DE,列出关于x的方程,进行计算即可解答;
(2)根据测量时需要注意的事项,即可解答.
本题考查了解直角三角形的应用−仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
25.【答案】(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ABC∽△ACD;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵∠BFE=∠A,
∴∠BFE=∠C,
又∵∠FBE=∠CBF,
∴△BFE∽△BCF,
∴BFBC=BEBF,
∴BC=BF2BE=423=163,
∴AD=163;
(3)如图,分别延长EF,DC相交于点G,
∵四边形ABCD是菱形,
∴AB//DC,∠BAC=12∠BAD,
∵AC//EF,
∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,
∵∠EDF=12∠BAD,
∴∠EDF=∠BAC,
∴∠EDF=∠G,
又∵∠DEF=∠GED,
∴△EDF∽△EGD,
∴EDEG=EFDE,
∴DE2=EF⋅EG,
又∵EG=AC=2EF,
∴DE2=2EF2,
∴DE= 2EF,
又∵DGDF=DEEF,
∴DG= 2DF=5 2,
∴DC=DG−CG=5 2−2.
【解析】(1)由∠ACD=∠B,∠A=∠A,推出△ABC∽△ACD;
(2)四边形ABCD是平行四边形,∠BFE=∠C,∠FBE=∠CBF,推出△BFE∽△BCF,线段成比例,求出BC,进而求出AD;
(3)延长EF,DC相交于点G,四边形ABCD是菱形,推出四边形AEGC为平行四边形,∠EDF=∠G,∠DEF=∠GED,推出△EDF∽△EGD,线段成比例,推出DG,进而求出DC.
本题考查平行四边形,菱形,三角形相似等综合问题,解题的关键是对三角形相似知识的熟练掌握.
26.【答案】解:(1)由题意得:−b2=11−b+c=0,
解得b=−2c=−3,
∴二次函数的表达式为y=x2−2x−3.
(2)如图所示:
CP的长为3− 3或3 3−3.
(3)若a≤1,
则当x=a时,函数有最小值:a2−2a−3=2a,
解得a=2± 7,
∵a≤1,
∴a=2− 7,
若a−1<1
解得:a=−2(舍去);
若a≥1,
则当x=a−1时,函数有最小值:(a−1)2−2(a−1)−3=2a,
解得a=0或6;
∵a>1,
∴a=6.
综上,a的值为2− 7或6.
【解析】(1)先根据题意得出点B的坐标,再利用待定系数法求解可得;
(2)分点P在点C上方和下方两种情况,先求出∠OBP的度数,再利用三角函数求出OP的长,从而得出答案;
(3)分对称轴x=1在a−1到a范围的右侧、中间和左侧三种情况,结合二次函数的性质求解可得.
本题考查二次函数的综合应用,掌握待定系数法求函数解析式、二次函数的图象与性质及分类讨论思想的运用是解题的关键.
2023年广西南宁市兴宁区中考数学三模试卷(含解析): 这是一份2023年广西南宁市兴宁区中考数学三模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广西南宁市兴宁区新民中学、第一十七中、第四十七中七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年广西南宁市兴宁区新民中学、第一十七中、第四十七中七年级(下)期中数学试卷(含解析),共24页。试卷主要包含了选择题,羊二,直金十两,牛二,填空题,解答题等内容,欢迎下载使用。
广西南宁市新民中学2021-2022学年中考数学对点突破模拟试卷含解析: 这是一份广西南宁市新民中学2021-2022学年中考数学对点突破模拟试卷含解析,共26页。试卷主要包含了不等式组的解集在数轴上表示为等内容,欢迎下载使用。












