


高考物理复习 课时过关题17 动能定理及其应用(含答案解析
展开2020(人教版)高考物理复习 课时过关题17
动能定理及其应用
1.高铁列车在启动阶段的运动可看作初速度为零的匀加速直线运动.在启动阶段,列车的动能( )
A.与它所经历的时间成正比
B.与它的位移成正比
C.与它的速度成正比
D.与它的动量成正比
A.动能增加了1 900 J
B.动能增加了2 000 J
C.重力势能减少了1 900 J
D.重力势能减少了2 000 J
3.将一小球竖直向上抛出,小球在运动过程中所受到的空气阻力不可忽略.a为小球运动轨迹上的一点,小球上升和下降经过a点时的动能分别为Ek1和Ek2,从抛出开始到小球第一次经过a点时重力所做的功为W1,从抛出开始到小球第二次经过a点时重力所做的功为W2.下列选项正确的是( )
A.Ek1=Ek2,W1=W2
B.Ek1>Ek2,W1=W2
C.Ek1<Ek2,W1<W2
D.Ek1>Ek2,W1<W2
4.如图所示,AB为圆弧轨道,BC为水平直轨道,圆弧的半径为R,BC的长度也是R,一质量为m的物体,与两个轨道间的动摩擦因数都为μ,当它由轨道顶端A从静止开始下落,恰好运动到C处停止,则物体在AB段克服摩擦力做的功为( )
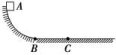
A.μmgR B.mgR C.mgR D.(1-μ)mgR
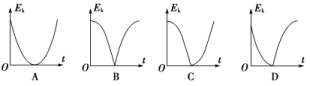
5.从地面竖直向上抛出一只小球,小球运动一段时间后落回地面.忽略空气阻力,该过程中小球的动能Ek与时间t的关系图象是( )
6.如图所示,长为L=1 m的长木板水平放置,在木板的A端放置一质量为m=1 kg的小物块,现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α=30°时,小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v=2 m/s,重力加速度g=10 m/s2,则在整个过程中( )
![]()
A.木板对小物块做的功为5 J
B.摩擦力对小物块做的功为5 J
C.支持力对小物块做的功为0
D.小物块克服摩擦力做的功为3 J
7.水平面上甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下停下来.甲、乙两物体的动能Ek随位移大小s的变化的图象如图所示,则下列说法正确的是( )
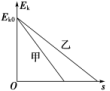
A.若甲、乙两物体与水平面动摩擦因数相同,则甲的质量较大
B.若甲、乙两物体与水平面动摩擦因数相同,则乙的质量较大
C.甲与地面间的动摩擦因数一定大于乙与地面的动摩擦因数
D.甲与地面间的动摩擦因数一定小于乙与地面的动摩擦因数
8.如图所示,两个半径不等的光滑半圆形轨道竖直固定放置,轨道两端等高,两个质量不等的球(从半径大的轨道下落的小球质量大,设为大球,另一个为小球,且均可视为质点)分别自轨道左端由静止开始下落,在各自轨迹的最低点时,下列说法正确的是( )
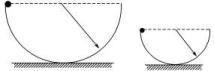
A.大球的速度可能小于小球的速度
B.大球的动能可能小于小球的动能
C.大球所受轨道的支持力等于小球所受轨道的支持力
D.大球的向心加速度等于小球的向心加速度
9.质量m=10 kg的物体只在变力F作用下沿水平方向做直线运动,F随坐标x的变化关系如图所示.若物体从坐标原点处由静止出发,则物体运动到x=16 m处时的速度大小为( )
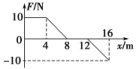
A.3 m/s B.4 m/s C.2 m/s D. m/s
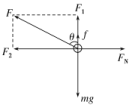
10.如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h,此为过程Ⅰ;若圆环在C处获得一竖直向上的速度v,则恰好能回到A处,此为过程Ⅱ.已知弹簧始终在弹性范围内,重力加速度为g,则圆环( )
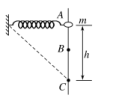
A.在过程Ⅰ中,加速度一直减小
B.在过程Ⅱ中,克服摩擦力做的功为mv2
C.在C处,弹簧的弹性势能为mv2-mgh
D.在过程Ⅰ、过程Ⅱ中克服摩擦力做功相同
11. (多选)如图所示,斜面体由粗糙程度不同的材料A、B拼接而成,其截面△OCD为等腰直角三角形,P为两材料在CD边上的交点,且DP>CP.现将OD边水平放置,让小物块无初速度地从C滑到D,然后将OC边水平放置,再让小物块无初速度地从D滑到C,小物块两次滑到P点的时间相同.下列说法正确的是( )
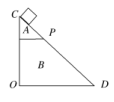
A.物块第二次滑到P点的速率大
B.两次滑动中物块到达P点时的速度大小相等
C.两次滑动中物块到达底端时的速度大小相等
D.物块第一次滑到P点的速率大
12. (多选)如图所示,质量为m的小球从A点由静止开始,沿竖直平面内固定光滑的圆弧轨道AB滑下,从B端水平飞出,恰好落到斜面BC的底端.已知圆弧轨道的半径为R,OA为水平半径,斜面倾角为θ,重力加速度为g.则( )
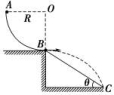
A.小球下滑到B点时对圆弧轨道的压力大小为2mg
B.小球下滑到B点时的速度大小为
C.小球落到斜面底端时的速度方向与水平方向的夹角为2θ
D.斜面的高度为4Rtan2θ
13.如图,在竖直平面内有由圆弧AB和圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接.AB弧的半径为R,BC弧的半径为.一小球在A点正上方与A相距处由静止开始自由下落,经A点沿圆弧轨道运动.
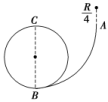
(1)求小球在B、A两点的动能之比.
(2)通过计算判断小球能否沿轨道运动到C点.
14.如图是翻滚过山车的模型,光滑的竖直圆轨道半径R=2 m,入口的平直轨道AC和出口的平直轨道CD均是粗糙的,质量m=2 kg的小车与水平轨道之间的动摩擦因数均为μ=0.5,加速阶段AB的长度l=3 m,小车从A点由静止开始受到水平拉力F=60 N的作用,在B点撤去拉力,取g=10 m/s2.试问:
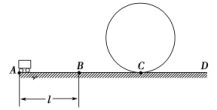
(1)要使小车恰好通过圆轨道的最高点,小车在C点的速度为多少?
(2)满足(1)问条件下,小车能沿着出口平直轨道CD滑行多远的距离?
(3)要使小车不脱离轨道,求平直轨道BC段的长度范围.
解析:[设列车运动时间为t,由匀变速直线运动规律v=at、x=at2,结合动能公式Ek=得Ek=、Ek=max,可知Ek∝v2、Ek∝t2、Ek∝x,故A、C项均错误,B项正确.由Ek=,得Ek∝p2,故D项错误.]
解析:根据动能定理,物体动能的增量等于物体所受所有力做功的代数和,
即ΔEk=WG+Wf=1 900 J-100 J=1 800 J,A、B项错误;
重力做功与重力势能改变量的关系为WG=-ΔEp,即重力势能减少了1 900 J,C项正确,D项错误.
解析:[从抛出开始到第一次经过a点和从抛出开始第二次经过a点,上升的高度相等,可知重力做功相等,即W1=W2,对两次经过a点的过程由动能定理得,-Wf=Ek2-Ek1,可知Ek1>Ek2,故B正确,A、C、D错误.]
解析:[全程对物体由动能定理得,mgR-W-μmgR=0,解得W=(1-μ)mgR,故D正确.]
解析:[设小球初动能为Ek0,初速度为v0,重力加速度为g.瞬时动能Ek=Ek0-mgh,h=v0t-gt2,联立得Ek=mg2t2-mgv0t+Ek0,故A正确.]
解析:设在整个过程中,木板对物块做的功为W,根据动能定理得:W=mv2=×1×22 J=2 J,
故A错误;在木板从水平位置开始转动到与水平面的夹角为30°的过程中,摩擦力不做功,
物块沿木板下滑过程中,摩擦力对物块做功,由于摩擦力小于重力沿木板向下的分力,
即f<mgsin30°,则摩擦力对物块做的功Wf=-fL≠-mgLsin30°=-5 J,故B错误;
在木板从水平位置开始转动到与水平面的夹角为30°的过程中,支持力对物块做的功设为WN,
根据动能定理得:WN-mgLsin30°=0,得WN=5 J,故C错误;在物块下滑的过程中,
根据动能定理得:mgLsin30°+Wf=mv2-0,得Wf=-3 J,
即小物块克服摩擦力做的功为3 J,故D正确.
解析:[甲、乙两物体的初动能和末动能都相同,都只受摩擦力作用,根据动能定理可知摩擦力对甲、乙两物体做的功相等,即μ甲m甲gs甲=μ乙m乙gs乙,由图可知s甲<s乙,所以μ甲m甲g>μ乙m乙g,即甲所受的摩擦力一定比乙大,若甲、乙两物体与水平面动摩擦因数相同,由Ff=μmg可知,则甲的质量较大,故A正确,B错误;μ甲m甲g>μ乙m乙g,由于质量关系未知,故无法直接确定动摩擦因数之间的关系,故C、D错误.]
解析:[由动能定理得mgR=mv2-0,解得v=,半径大的圆形轨道,球到达底端时的速度大,所以大球的速度一定大于小球的速度,故A错误;大球质量大,到达底端时的速度大,动能一定大,故B错误;根据a==2g知,两球的向心加速度相等,故D正确;在底端时,由牛顿第二定律得,FN-mg=ma,解得FN=3mg,由于大球的质量大,则大球所受的支持力大,故C错误.]
解析:[Fx图线与x轴围成的面积表示力F所做的功,则这段过程中,外力做功为W=×(4+8)×10 J-×4×10 J=40 J,根据动能定理得W=mv2,解得v== m/s=2 m/s,故C正确,A、B、D错误.]
解析:圆环刚开始下滑时,圆环受到的合力向下,设弹簧原长为L,下滑过程中,对圆环受力分析,如图所示,弹簧弹力与竖直方向的夹角为θ,则弹簧弹力F=kL,竖直方向根据牛顿第二定律可得mg-Fcosθ-μFN=ma,水平方向有Fsinθ=FN,联立三个方程可知,圆环下滑过程中受到的合力先减小后增大,圆环的加速度先减小后增大,选项A错误;在过程Ⅰ和Ⅱ中,圆环在相同位置时受到的滑动摩擦力大小相等,所以在这两个过程中克服摩擦力做的功相等,选项D正确;在过程Ⅰ中,根据动能定理可得WG-Wf-W弹=0,解得Wf=WG-W弹,在过程Ⅱ中,根据动能定理可得-WG+W弹-Wf=-mv2,联立解得Wf=mv2,在C处Ep弹=W弹=mgh-mv2,选项B、C错误.
解析:由题意可知,小物块两次滑到P点的时间相同,由于DP>CP,因此从D到P的平均速度大于从C到P的平均速度,设从C滑到P点时速度为v1,从D滑到P点时速度为v2,则根据匀变速直线运动知识有:>,即从D滑到P点时的速度大于从C滑到P点时的速度,故A正确,B、D错误;小物块从D到C和从C到D的过程中摩擦力做的功相等,重力做的功相等,根据动能定理可知,两次滑动中物块到达底端的速度大小相等,故C正确.
解析:[小球由A至B的过程由动能定理得,mgR=mv2-0,解得v=,小球通过B点时,由牛顿第二定律得FN-mg=m,解得FN=3mg,根据牛顿第三定律可知,在B点小球对轨道的压力大小为3mg,故A错误,B正确;小球从B到C做平抛运动,则有tan θ==,解得t=,小球落到斜面底端时的速度方向与水平方向的夹角正切为tan α==2tan θ,则α≠2θ,故C错误;斜面的高度为h=gt2=g2=4Rtan2θ,故D正确.]
(1)小球下落过程由动能定理得:小球下落至A点的过程:mg·=EkA-0
小球下落至B点的过程:mg=EkB-0
由以上两式联立解得:=5
(2)小球恰好经过C点时,由牛顿第二定律得:mg=m解得:v0=
小球由开始下落至C点的过程,由动能定理得:mg·=mv-0解得:vC=
由于vC=v0,故小球恰好可以沿轨道运动到C点.
(1)设小车恰好通过最高点的速度为v0,则有mg=①
由C点到最高点满足机械能守恒定律,有mv=mg·2R+mv②
解得vC=10 m/s
(2)小车由最高点滑下到最终停在轨道CD上,由动能定理有mg·2R-μmgxCD=0-mv③
联立①③解得xCD=10 m
(3)小车经过C点的速度vC≥10 m/s就能做完整的圆周运动.
小车由A到C由动能定理得Fl-μmg(l+xBC)=mv
解得xBC≤5 m
小车进入圆轨道时,上升的高度h≤R=2 m时,小车返回而不会脱离轨道,
由动能定理有Fl-μmg(l+xBC)-mgh=0
解得xBC≥11 m
综上可得,xBC≤5 m或者xBC≥11 m时小车不脱离轨道.
高考物理复习 课时过关题20 动量守恒定律及其应用(含答案解析): 这是一份高考物理复习 课时过关题20 动量守恒定律及其应用(含答案解析),共8页。试卷主要包含了7×102 kg·m/s,0×102 kg·m/s,2v B.0等内容,欢迎下载使用。
高考物理一轮复习课时作业17动能定理及其应用含答案: 这是一份高考物理一轮复习课时作业17动能定理及其应用含答案
高考物理一轮复习课时作业17动能定理及其应用含答案: 这是一份高考物理一轮复习课时作业17动能定理及其应用含答案












