苏科版九年级上册第2章 对称图形——圆2.5 直线与圆的位置关系当堂达标检测题

这是一份苏科版九年级上册第2章 对称图形——圆2.5 直线与圆的位置关系当堂达标检测题，共27页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
专题2.23 切线的性质与判定（基础练）
一、单选题
1．在中，，，，以C为圆心作与AB相切，则的半径长为（    ）
A．8 B．4 C．9.6 D．4.8
2．下列直线是圆的切线的是（    ）
A．经过半径外端的直线 B．垂直于半径的直线
C．与圆有公共点的直线 D．圆心到直线的距离等于这个圆的半径长的直线
3．如图，内接于，过A点作直线，当（    ）时，直线与相切．

A． B． C． D．
4．用直角钢尺检查下列工件是否恰好是半圆环形，则根据图示情况，肯定是半圆环形的工件是（   ）
A．   B．  C．   D．  
5．如图，点A在上，下列条件不能说明是切线的是（    ）

A． B．
C． D．
6．如图，是的直径，C、D是上的点，，过点C作的切线交的延长线于点E，则等于（　　）
  
A． B． C． D．
7．如图，在中，为弦，于点，，过点作的切线，交的延长线于点，则(    )
  
A． B． C． D．
8．如图，是的直径，，垂足为E，直线与相切于点C，交于点D，直线交的延长线于点P，连接，若，则的度数是（    ）

A． B． C． D．
9．如图，已知PA与⊙O相切于点A，连接OA，AB是⊙O的弦，且AB⊥OP，垂足为点C．若AP＝3，OP＝3，则OC的长为（　　）

A． B． C．2 D．
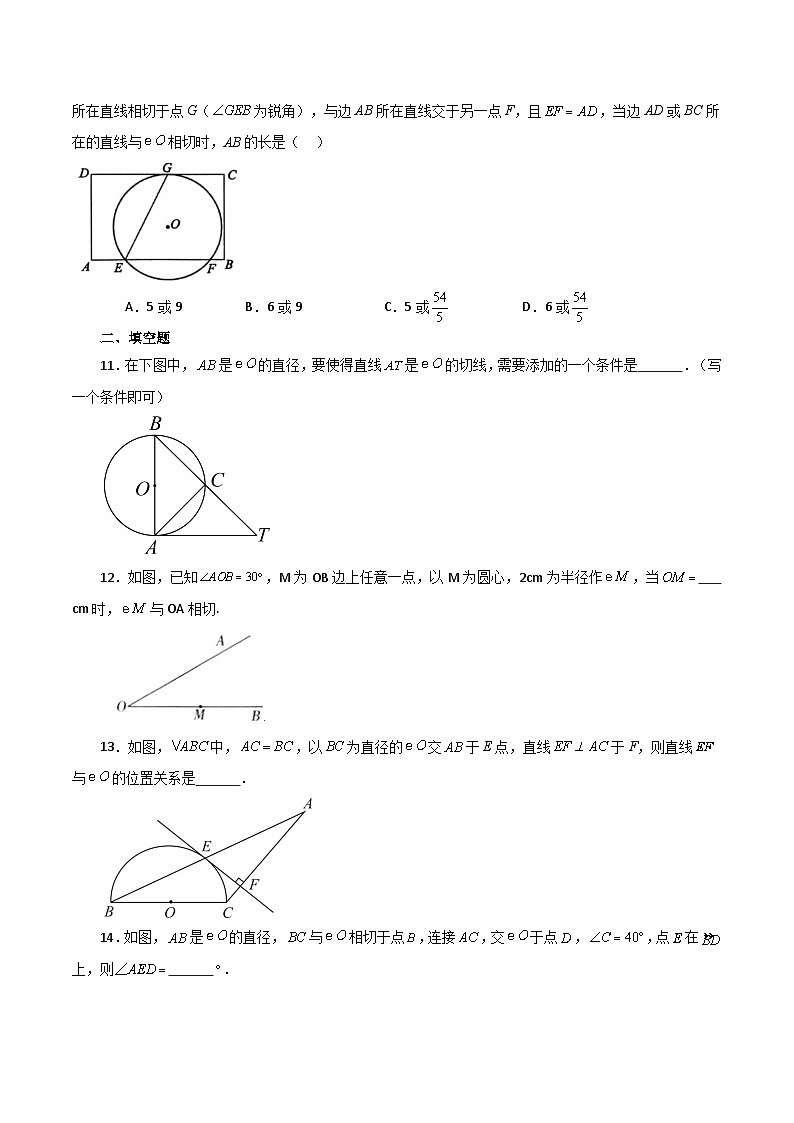
10．如图，在矩形ABCD中，，E是边AB上一点，且．已知经过点E，与边CD所在直线相切于点G（为锐角），与边AB所在直线交于另一点F，且，当边AD或BC所在的直线与相切时，AB的长是（    ）

A．5或9 B．6或9 C．5或 D．6或
二、填空题
11．在下图中，是的直径，要使得直线是的切线，需要添加的一个条件是 ．（写一个条件即可）

12．如图，已知，M为OB边上任意一点，以M为圆心，2cm为半径作，当 cm时，与OA相切.

13．如图，中，，以为直径的交于E点，直线于F，则直线与的位置关系是 ．

14．如图，是的直径，与相切于点，连接，交于点，，点在上，则 ．
  
15．如图，圆内接四边形的边过圆心O，过点C的切线与边所在直线垂直于点M，若，则等于 ．
  
16．如图，在中，，与它的边，相切，射线交边于点．当，时，的长等于
  
17．如图，切于A点，连接交于点C，点D是优弧上一点，若为α，则 （用含α的代数式表示）．
  
18．如图，在平面直角坐标系xOy中，直线AB经过点A(−6，0)，B(0，6)，⊙O的半径为2（O为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为

三、解答题
19．如图，已知内接于，是的直径，的平分线交于点，交于点，连接，作，交的延长线于点．
(1)求证：是的切线；
(2)若，，求的半径．








20．如图，在中，为的直径，为弦、，．
(1)求的度数；
(2)在图（1）中，P为直径的延长线上一点，且，求证：为的切线．






21．如图，点A在第一象限内，与x轴相切于点B，与y轴相交于点C，D，连结，过点作于点H．
(1)求证：四边形为矩形．
(2)已知的半径为4，，求弦的长．






22．已知：如图，在中，，D是的中点．以为直径作，交边于点P，连接，交于点E．
(1)求证：是的切线；
(2)若是的切线，，求的长．







23．如图1，已知为的直径，点E在上，给出下列信息：①是的切线；②；③平分
(1)请在上述3条信息中选择其中两条作为条件，剩余的一条信息作为结论，组成一个正确的命题，你选择的条件是 、 ，结论是 (只要填写序号)，并说明理由；
(2)如图2，在（1）的条件下，交于D，若，求的值．





24．如图1，是的直径，点C是上一点（不与点A，B重合），连接．
(1)请在图1中用无刻度的直尺和圆规作出的中点．（点C，D在线段AB异侧）；（保留作图痕迹，不写作法）
(2)如图2，在（1）的条件下，过点D作的切线，分别交的延长线于点E，F．
①求证：；
②过C作于M，交于点N，若，，求的长．









参考答案
1．D
【分析】过点C作CD⊥AB于点D，先利用勾股定理求得BC的长，再利用三角形的面积公式求得CD的长即可.
解：如图，过点C作CD⊥AB于点D，
∵，，，
∴，
∵S△ABC，
∴，
则以C为圆心CD为半径作与AB相切.
故选D.

【点拨】本题主要考查切线的判定，勾股定理，三角形的面积公式，解此题的关键在于熟练掌握其知识点.
2．D
【分析】根据圆的切线的判定定理进行判断即可.
解：A. 经过半径外端的直线，但直线不一定垂直半径，故不能判断该直线是圆的切线；
B. 垂直于半径的直线，但直线不是经过半径外端，故不能判断该直线是圆的切线；
C. 与圆有公共点的直线，直线与圆相交也有公共点，故不能判断该直线是圆的切线；
D. 圆心到直线的距离等于这个圆的半径长的直线，能判断该直线是圆的切线.
故选D.
【点拨】本题主要考查圆的切线的判定定理，圆的切线必须与半径垂直，且过半径的外端.
3．C
【分析】首先过点O作直径AF，连接BF，根据同弧所对的圆周角相等可得∠C＝∠AFB，进而可得到∠BAE＝∠F，再根据直径所对的圆周角是90°，可证出∠AFB+∠BAF＝90°，再利用等量代换可得∠BAE+∠BAF＝90°，进而得到直线DE与⊙O相切．
解：当时，直线与相切．
理由如下：
作AF交圆O于F点，连接BF．
∵∠F，∠C是同弧AB所对的角，
∴∠C＝∠F，
∵∠BAE＝∠C，
∴∠BAE＝∠F，
∵AF为直径，
∴∠ABF＝90°，
∴在三角形ABF中，∠F+∠BAF＝90°，
∵∠F＝∠BAE，
∴∠BAE+∠BAF＝90°，
∴FA⊥DE，
∴直线DE与⊙O相切．
故选：C
．
【点拨】此题主要考查了切线的判定，关键是正确作出辅助线，证明∠BAE+∠BAF＝90°．
4．B
【分析】根据切线性质和的圆周角所对的弦是直径可得答案．
解：A、不能保证弦的另一端与圆相切，即不能保证弦为直径，故不能肯定是半圆环形的工件，不符合题意；
B、图中角是圆周角，故能肯定是半圆环形的工件，符合题意；
C、图中角不是圆周角，故不能肯定是半圆环形的工件，不符合题意；
D、图中角不是圆周角，故不能肯定是半圆环形的工件，不符合题意；
【点拨】本题考查圆周角定理、切线性质，熟知的圆周角所对的弦是直径是解答的关键．
5．D
【分析】根据切线的判定定理即可依次判断．
解：A. 由可得AO⊥AP，可判定是切线；，
B. 可判定是切线；
C. 由，可得∠PAO=90°，可判定是切线；
D. 不能判定是切线；
故选D．

【点拨】此题主要考查切线的判定，解题的关键是熟知圆的切线判定定理．
6．A
【分析】如图，连接，由是的切线，可得，，由，可得．
解：如图，连接，
  
∵是的切线，
∴，
∴，
∵，
∴，
故选：A．
【点拨】本题考查了切线的性质，圆周角定理，三角形内角和定理．解题的关键在于对知识的熟练掌握．
7．B
【分析】连接，根据等腰三角形的性质得到，由切线的性质得到，于是得到结论．
解：于，，
，
是的切线，
，
，
故选：B．
【点拨】本题考查了切线的性质，等腰三角形的性质，正确的作出辅助线构造直角三角形是解题的关键．
8．A
【分析】根据切线的性质和已知求得，由圆周角定理求得，根据圆的性质求得，结合已知得到，利用平行线的性质从而求出结果．
解：连接，

直线与相切于点C，
，
，
，
，
，
，
，
又，，
，
，
故选：A．
【点拨】本题考查了切线的性质，三角形内角和定理，圆周角定理，圆的性质和平行线的判定和性质；利用以上性质对角进行转换是解题的关键．
9．A
【分析】由勾股定理可知OA＝3，从而可知∠AOC＝45°，所以△OAC是等腰直角三角形，利用勾股定理即可求出OC的长度．
解：∵AP是⊙O的切线，
∴∠OAP＝90°，
∵AP＝3，OP＝3，
∴由勾股定理可知：OA＝=3，
∴∠AOC＝45°，
∵AB⊥OP，
∴∠OCA＝90°，
∴△AOC是等腰直角三角形，OC=AC
∵AO=
∴OC＝OA＝，
故选：A．

【点拨】此题主要考查切线的性质定理及应用，解题的关键是熟知垂径定理与切线的性质．
10．D
【分析】边BC所在的直线与⊙O相切时，过点G作GN⊥AB，垂足为N，可得EN＝NF，由，依据勾股定理求出半径r，根据计算即可；当边AD所在的直线与⊙O相切时，同理可求．
解：边BC所在的直线与⊙O相切时，
如图，

切点为K，连接OK，过点G作GN⊥AB，垂足为N，
∴EN＝NF，
又∵，
∴
设⊙O的半径为r，由OE2＝EN2＋ON2，
得：r2＝16＋（8−r）2，
∴r＝5，
∴OK＝NB＝5，
∴EB＝9，
又，即，
∴AB＝；
当边AD所在的直线与⊙O相切时，切点为H，连接OH，过点G作GN⊥AB，垂足为N，

同理，可得OH＝AN＝5，
∴AE＝1，
又，
∴AB＝6，
故选：C．
【点拨】本题考查了切线的性质、勾股定理和垂径定理的综合应用，解答本题的关键在于做好辅助线，利用勾股定理求出对应圆的半径．
11．∠ABT=∠ATB=45°（答案不唯一）
【分析】根据切线的判定条件，只需要得到∠BAT=90°即可求解，因此只需要添加条件：∠ABT=∠ATB=45°即可．
解：添加条件：∠ABT=∠ATB=45°，
∵∠ABT=∠ATB=45°，
∴∠BAT=90°，
又∵AB是圆O的直径，
∴AT是圆O的切线，
故答案为：∠ABT=∠ATB=45°（答案不唯一）．

【点拨】本题主要考查了圆切线的判定，三角形内角和定理，熟知圆切线的判定条件是解题的关键．
12．4
【分析】过M作MN⊥OA于点N，此时以MN为半径的圆与OA相切，根据30°角所对直角边为斜边的一半可得OM的长.
解：如图，过M作MN⊥OA于点N，
∵MN=2cm，，
∴OM=4cm，
则当OM=4cm时，与OA相切.
故答案为4.

【点拨】本题主要考查切线判定，直角三角形中30°角所对直角边为斜边的一半，解此题的关键在于熟练掌握其知识点.
13．相切
【分析】连接，，由为圆的直径，根据直径所对的圆周角为直角可得为直角，利用垂直的定义可得垂直于，又，根据三线合一得到为的中点，又为直径的中点，可得为三角形的中位线，根据三角形的中位线平行与第三边可得与平行，同时由与垂直，得到为直角，根据两直线平行内错角相等可得为直角，可得为圆的切线，得证．
解：证明：连接，，

为圆的直径，
，
，又，
为的中点，又为直径的中点，
为的中位线，
，
，
又，，
，
则为圆的切线．
故答案为：相切．
【点拨】此题考查了切线的判定，涉及的知识有：等腰三角形的性质，圆周角定理，平行线的性质，以及切线的判定定理，切线的判定定理是经过直径的外端点，且与直径垂直的直线为圆的切线，熟练掌握此定理是证明的关键．
14．
【分析】如图所示，连接，由切线的性质得到，进而求出，由是的直径，得到，则，再由同弧所对的圆周角相等即可得到．
解：如图所示，连接，
    
∵与相切于点，
∴，
∵，
∴，
∵是的直径，
∴，
∴，
∴，
故答案为：．
【点拨】本题主要考查了切线的性质，圆周角定理，直角三角形的性质等等，正确作出辅助线是解题的关键．
15．/20度
【分析】由圆内接四边形的性质求出，由圆周角定理求出，得出，由过点C的切线与边所在直线垂直于点M，可得，，继而根据三角形的外角性质得出，即可求出的度数．
解：连接，
  
∵圆内接四边形的边过圆心O，
∴，
∴，，
∵过点C的切线与边所在直线垂直于点M，
∴，
∵，
∴，
∴，，
∵，
∴，
∴，
故答案为：．
【点拨】本题考查了圆内接四边形的性质、圆周角定理、三角形的外角性质等知识；熟练掌握圆内接四边形的性质和圆周角定理是解决问题的关键．
16．2
【分析】根据切线的性质和角平分线的性质可得，根据平行四边形的性质可得，即可推得，根据等角对等边可得，即可求得．
解：∵与它的边，相切，
∴点到，的距离相等，
∴是的角平分线，
∴，
∵四边形是平行四边形，
∴，
∴，
∴，
∴，
故，
故答案为：2．
【点拨】本题考查了切线的性质，角平分线的性质，平行四边形的性质，等角对等边，熟练掌握以上性质是解题的关键．
17．
【分析】连接，根据切线的性质，得到，进而得到，再利用圆周角定理即可得解．
解：连接，
  
∵切于A点，
∴，
∵为α，
∴，
∴．
故答案为：．
【点拨】本题考查切线的性质，圆周角定理．熟练掌握圆的切线垂直于过切点的半径，同弧所对的圆周角等于圆心角的一半，是解题的关键．
18．
【分析】连接OP．根据勾股定理知PQ2=OP2-OQ2，当OP⊥AB时，线段OP最短，即线段PQ最短．
解：连接OP、OQ．
∵PQ是⊙O的切线，
∴OQ⊥PQ；
根据勾股定理知PQ2=OP2-OQ2，
∵当PO⊥AB时，线段PQ最短；
又∵A（-6，0）、B（0，6），
∴OA=OB=6，
∴AB=6，
∴OP=AB=3，
∵OQ=2，
∴PQ=，
故答案为：．

【点拨】本题考查了切线的判定与性质、坐标与图形性质以及矩形的性质等知识点．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角来解决有关问题．
19．（1）见分析；（2）15
【分析】（1）连接，根据平分，，，证明即可；
（2）设的半径为，则有，在中，，根据勾股定理建立方程，解方程即可求解．
（1）解：连接，
  
是的直径，
，即，
平分，
，
，
，
，
，
，
，
是的半径，
是的切线．
（2）设的半径为，
则有，
∵是的切线．
∴，
在中，，
，
解得，
的半径为．
【点拨】本题考查了切线的性质与判定，勾股定理，熟练掌握切线的性质与判定是解题的关键．
20．（1）；（2）见分析
【分析】（1）根据圆的基本性质以及等边三角形的判定与性质求解即可；
（2）作于点，通过面积计算确定，从而求得，进而证得，最终结合点为半径的外端点，证得结论．
（1）解：在中，，则为等腰三角形，
∵，
∴为等边三角形，
∴；
（2）证：如图所示，作于点，
  
由（1）知为等边三角形，
∵，
∴，，
∵，，
∴，即：，
∴，
∵，，
∴，
∵，
∴，
∴，
∵点为半径的外端点，
∴为的切线．
【点拨】本题考查圆的基本性质，等边三角形的判定与性质，切线的判定等，掌握圆的基本性质以及切线的判定方法是解题关键．
21．（1）详见分析；（2）6
【分析】（1）根据切线的性质得到轴根据垂直的定义得到，根据矩形的判定定理得到四边形是矩形；
（2）连接，根据矩形的性质得到，根据勾股定理得到，根据垂径定理即可得到结论．
解：（1）证明：与轴相切于点，
轴
又，，
，
四边形是矩形；
（2）解：连接，
  
四边形是矩形，
，
，
，
，
．
【点拨】本题考查了切线的性质，矩形的判定和性质，勾股定理，垂径定理，正确作出辅助线是解题的关键．
22．（1）证明见分析；（2）
【分析】（1）要证明是圆O的切线，只要证明即可；
（2）连接，根据等腰三角形的性质求得的长，再求的长，根据切线的性质求得，最后利用勾股定理求出的长．
解：（1）证明：∵，D是的中点，
∴．
又∵是直径，
∴是的切线．
（2）解：连接.

∵点D是边的中点，，
∴，
∴．
∴，
∵是的切线，O为圆心，
∴．
在中，由勾股定理，得，
∴．
【点拨】本题是圆的综合问题，考查了圆的切线的判定与性质，勾股定理，等腰三角形的性质，掌握这些性质是解决本题的关键．
23．（1）选择的条件是①②，结论是③，理由见分析；选择的条件是①③，结论是②，理由见分析；选择的条件是②③，结论是①，理由见分析；（2）
【分析】（1）选择的条件是①②，结论是③，理由：连接，可得到，再由是的切线可得，从而得到，即可；选择的条件是①③，结论是②，理由：连接，可得到，再由平分可证得，再由是的切线，即可；选择的条件是②③，结论是①，理由：连接，可得到，再由平分可证得，从而得到，即可；
（2）连接，根据圆内接四边形的性质可得，再证得，可得到，从而求出，即可求解．
（1）解：选择的条件是①②，结论是③，理由如下：
连接，

，
．
是的切线，
．
，
．
，
，
平分．
选择的条件是①③，结论是②，理由如下：
连接，

，
．
平分，
，
，
．
是的切线，
．
；
选择的条件是②③，结论是①，理由如下：
连接，

，
．
平分，
，
，
．
，
．
是半径，
是的切线；
（2）解：如图，连接，

∵四边形是圆内接四边形，
∴，
∵，
∴，
，为的直径，
∴，
平分，
，
∴，
∴，
∵，
∴，
∴，
∵，
∴，解得：或（舍去），
∴，
∴．
【点拨】本题主要考查了切线的性质和判定，圆内接四边形的性质，相似三角形的判定和性质等知识，熟练掌握切线的性质和判定，圆内接四边形的性质，相似三角形的判定和性质是解题的关键．
24．（1）见分析；（2）①见分析；②
【分析】（1）根据角平分线的画法求解即可；
（2）①连接，由圆周角定理证出，由切线的性质得出，则可得出结论；
②过点作于，交于，证出四边形是矩形，得出，求出的长，则由可得出答案．
（1）解：如图1，
  ；  
（2）①证明：连接，
  
平分，
，
，
，
又是的切线，
，
，
∴；
②过点作于，交于，
，，
，
又，
四边形是矩形，
，
是的直径，，，
，
，
，
，
．
【点拨】此题是圆的综合题，考查了切线的性质、圆周角定理、勾股定理、三角形的面积等知识，熟记掌握切线的性质是解题的关键．