九上数学人教第二十一章单元测试卷
展开第二十一章 一元二次方程
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·北京西城区期中)若(m-1)x|m|+1-2x=3是关于x的一元二次方程,则m的值为 ( )
A.-1 B.1 C.±1 D.无法确定
2.(2023·广东珠海期中)把2x(x-1)=3x化成一元二次方程的一般形式,则二次项系数、一次项系数、常数项分别是 ( )
A.2,5,0 B.2,-5,1 C.2,-5,0 D.2,5,1
3.(2023·宁夏吴忠利通区期末)将一元二次方程x2+4x+2=0配方后,可得到方程 ( )
A.(x-2)2=2 B.(x+2)2=6
C.(x-2)2=6 D.(x+2)2=2
4.(2021·山东烟台模拟)若4a-2b+c=0,则一元二次方程ax2-bx+c=0(a≠0)必有一根是 ( )
A.0 B.无法确定 C.-2 D.2
5.若2x2+1与4x2-2x-5互为相反数,则x= ( )
A.-1或
B.1或- C.1或-
D.1或
6.(2023·河北保定市第十七中学月考)已知(x2+y2)2-y2=x2+6,则x2+y2= ( )
A.-2 B.3 C.-2或3 D.-3或2
7.(2023·河北唐山期中改编)小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=-1.他核对时发现所抄的c值比原方程的c值小2,则原方程的根的情况是 ( )
A.不存在实数根 B.有两个不相等的实数根
C.有一个根是x=-1 D.有两个相等的实数根
8.(2023·天津河西区期中改编)生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的支干后,每个支干又会长出同样数目的小分支.现有符合上述生长规律的某种植物,它的主干、支干和小分支的总数是91,则这种植物每个支干长出小分支的个数是 ( )
A.9 B.10 C.-10 D.9或10
9.(2023·湖北武汉武昌区期末)若实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a2+b2= ( )
A.36 B.50 C.28 D.25
- (2023·山西晋中期中)如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1 cm/s,点Q的速度为2 cm/s,点Q移动到点C处停止,点P也随之停止运动.当四边形APQC的面积为12 cm2时,点P运动的时间是 ( )
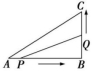A.6 s B.2 s或6 s
C.3 s D.2 s
二、填空题(共5小题,每小题3分,共15分)
11.(2021·辽宁锦州期末)已知关于x的一元二次方程x2-mx=0的一个根为1,则m= .
12.(2023·上海宝山区罗南中学月考)写出两根分别为1,2,且二次项系数为1的关于x的一元二次方程: .
13.(2023·云南文山期末)现规定一种新的运算:
=ad-bc,当
=2x时,x的值为 .
14.(2023·湖北孝感期中)若方程x2-2 023x+1=0的一个根为a,则a2-2 022a+
= .
15.(2023·江西南昌段考)在2023年7月的日历表上用一个方框圈出4个数(如图所示),若圈出的4个数中,最小数与最大数的乘积为180,则这个最小数为 .
三、解答题(共6小题,共55分)
16.(共3小题,每小题4分,共12分)用适当的方法解下列方程:
(1)y(y-1)=2-2y;
(2)5x2-8x=-5;
(3)(x+2)2-8(x+2)+15=0.
17.(8分)(2023·河北沧州段考改编)嘉嘉与淇淇两位同学解方程3(x-3)=(x-3)2的过程如下.
嘉嘉:两边同时除以(x-3),得3=x-3, 解得x=6. |
淇淇:移项,得3(x-3)-(x-3)2=0, 提取公因式,得(x-3)(3-x-3)=0. 则x-3=0或3-x-3=0, 解得x1=3,x2=0. |
(1)嘉嘉的解法 ,淇淇的解法 .(填“正确”或“不正确”)
(2)请你给出正确的解法,并结合你的经验提出一条解题注意事项.
18.(8分)(2023·湖南张家界期末改编)某校为响应全民阅读活动,在周六面向社会开放学校图书馆.据统计,该校图书馆第一个月进馆256人次,第三个月进馆576人次,假设进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳不超过1 000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否正常接纳第四个月的进馆人次?请说明理由.
19.(8分) 新风向 新定义试题(2023·江苏苏州期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,其中一个根比另一个根大1,那么称这样的方程为“邻根方程”.例如,一元二次方程x2+x=0的两个实数根分别是x1=0,x2=-1,则方程x2+x=0是“邻根方程”.
(1)通过计算,判断方程2x2-2
x+1=0是否是“邻根方程”.
(2)已知关于x的方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,求m的值.
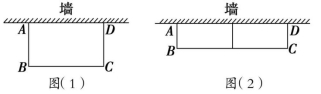
20.(9分)(2023·四川成都期中)如图(1),用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15 m,篱笆总长为24 m.
(1)若围成的花圃面积为40 m2,求BC的长;
(2)如图(2),若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃总面积为50 m2,则能否成功围成花圃?如果能,求BC的长;如果不能,请说明理由.
21.(10分) 新风向 探究性试题(2023·河南洛阳期中)阅读并完成下列问题:任意给定一个矩形A,是否存在另一矩形B,使它的周长和面积分别是已知矩形周长和面积的一半?
(1)当已知矩形A的两边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边长分别是x和y,由题意可得方程组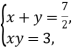
消去y,得2x2-7x+6=0.
∵Δ=49-48=1>0,
∴x1= ,x2= ,
∴满足要求的矩形B存在.
(2)如果已知矩形A的两边长分别为2和1,那么请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的两边长分别为m和n,那么请你研究当m,n满足什么条件时,矩形B存在,并说明理由.
第二十一章 一元二次方程答案
1.A 2.C 3.D 4.D 5.B 6.B 7.A 8.A 9.C 10.D
11.1 12.x2-3x+2=0
13.2或3 14.2 022 15.10
16.【参考答案】(1)移项,得y(y-1)+2(y-1)=0, (2分)
因式分解,得(y+2)(y-1)=0,
解得y1=-2,y2=1. (4分)
(2)移项,得5x2-8x+5=0.
因为a=5,b=-8,c=5,
所以Δ=b2-4ac=64-100=-36<0, (2分)
所以方程无实数根. (4分)
(3)(整体思想)把(x+2)看成一个整体,
因式分解,得[(x+2)-3][(x+2)-5]=0, (2分)
整理,得(x-1)(x-3)=0,
解得x1=1,x2=3. (4分)
17.【参考答案】(1)不正确 不正确 (2分)
(2)正确的解法是:3(x-3)=(x-3)2,
移项,得3(x-3)-(x-3)2=0,
提取公因式,得(x-3)(3-x+3)=0,
则x-3=0或3-x+3=0,
解得x1=3,x2=6. (6分)
18.【参考答案】(1)设进馆人次的月平均增长率为x,
根据题意得,256(1+x)2=576,
解得x1=0.5=50%,x2=-2.5(不合题意,舍去).
答:进馆人次的月平均增长率是50%. (4分)
(2)能. (5分)
理由:576×(1+50%)=864(人次),
∵864<1 000,
∴校图书馆能正常接纳第四个月的进馆人次. (8分)
19.【参考答案】(1)是. (1分)
理由:Δ=(-2)2-4×2×1=4>0,故方程有两个不相等的实数根.
解一元二次方程,得x1=
,x2=
. (2分)
∵-=1,
∴方程2x2-2x+1=0是“邻根方程”. (4分)
(2)解方程,得x=m或x=-1. (5分)
∵方程x2-(m-1)x-m=0(m是常数)是“邻根方程”,
∴|m-(-1)|=1,
∴m=-1+1或m=-1-1, (7分)
解得m=0或-2. (8分)
20.【参考答案】(1)设BC的长为x m,则AB的长为
m.
根据题意,得x·=40.
整理,得x2-24x+80=0. (2分)
解得x1=4,x2=20.
∵20>15,∴x2=20不符合题意,舍去,
∴BC的长为4 m. (4分)
(2)不能. (5分)
理由:设BC的长为y m,则AB的长为
m.
根据题意,得y·=50,
整理,得y2-24y+150=0. (7分)
∵Δ=(-24)2-4×1×150=-24<0,
∴该方程无实数根,
∴不能围成总面积为50 m2的花圃. (9分)
21.【参考答案】(1) 2 (2分)
(2)设所求矩形的两边长分别是a和b,
由题意,得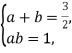
消去b,得2a2-3a+2=0.
∵Δ=9-16=-7<0,
∴不存在满足要求的矩形B. (5分)
(3)当m,n满足(m-n)2-4mn≥0时,矩形B存在.(6分)
理由如下:
设所求矩形的两边长分别是p和q,
由题意,得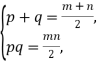
消去q,得2p2-(m+n)p+mn=0, (7分)
∴Δ=[-(m+n)]2-8mn=(m-n)2-4mn.
当Δ≥0时,存在满足要求的矩形B,
即当(m-n)2-4mn≥0时,矩形B存在. (10分)
