- 【同步学案】高中数学人教A版(2019)必修第一册--课时2.2 基本不等式 学案(Word版含答案) 学案 11 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时2.3 二次函数与一元二次方程、不等式 学案(Word版含答案) 学案 10 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时3.1.2 函数的表示方法 学案(Word版含解析) 学案 11 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时3.2 函数的基本性质 学案 2课时(Word版含答案) 学案 14 次下载
- 【同步学案】高中数学人教A版(2019)必修第一册--课时3.3 幂函数 学案(Word版含答案) 学案 13 次下载
【同步学案】高中数学人教A版(2019)必修第一册--课时3.1.1 函数的概念 学案(Word版含答案)
展开![]() 课时3.1.1 函数的概念
课时3.1.1 函数的概念
![]() 01考点梳理
01考点梳理
![]() 知识点一 函数的概念
知识点一 函数的概念
定义 | 一般地,设A,B是非空的 ,如果对于集合A中的 按照某种确定的对应关系f,在集合B中都有 的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数 | |
三要素 | 对应关系 | y=f(x),x∈A |
定义域 | 的取值范围 | |
值域 | 与x的值相对应的y的函数值的集合 | |
![]()
![]() 知识点二 区间及有关概念
知识点二 区间及有关概念
(1)一般区间的表示。设a,![]() b∈R,且a<b,规定如下:
b∈R,且a<b,规定如下:
定义 | 名称 | 符号 | 数轴表示 |
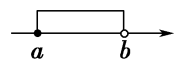
{x|a≤x≤b} | 闭区间 | __________________ |
|
{x|a<x<b} | 开区间 | __________________ |
|
{x|a≤x<b} | 半开半闭区间 | [a,b) |
|
{x|a<x≤b} | 半开半闭区间 | (a,b] |
|
![]() (2)特殊区间的表示
(2)特殊区间的表示
定义 | R | {x|x≥a} | {x|x>a} | {x|x≤a} | {x|x<a} |
符号 |
| [a,+∞) | (a,+∞) | (-∞,a] | (-∞,a) |
答案:实数集 任意一个数x 唯一确定 自变量x {f(x)|![]() x∈A} [a,b] (a,b) (-∞,+∞)
x∈A} [a,b] (a,b) (-∞,+∞)
![]() 02考点解读
02考点解读
![]() 题型一 对函数概念的理解
题型一 对函数概念的理解
![]() 1.下列图形中,不可能是函数图象的是( )
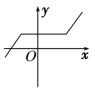
1.下列图形中,不可能是函数图象的是( )
A.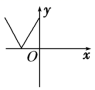 B.
B.![]()
 C.
C.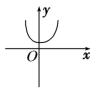 D.
D.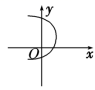
![]() 【答案】D
【答案】D
【解析】![]() 根据函数的定义,一个自变量
根据函数的定义,一个自变量![]() 对应唯一的函数值,
对应唯一的函数值,
![]() 表现在图像上,用一条垂直于
表现在图像上,用一条垂直于![]() 轴的直线交函数图像,至多有一个交点.
轴的直线交函数图像,至多有一个交点.
![]() 所以D不是函数图像.
所以D不是函数图像.
![]() 故选:D
故选:D
![]() 题型二 求解函数值
题型二 求解函数值
2.已知![]()
![]() ,则
,则![]() _________.
_________.
![]() 【答案】
【答案】![]()
【解析】![]() 因为
因为![]() ,
,
![]() 所以
所以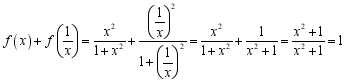
![]() 则
则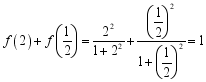 ,
,
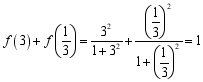
![]() ,
,![]() .
.
所以![]()
![]()
![]() .
.
![]() 故答案为:
故答案为:![]() .
.
![]() 题型三 函数定义域的求解
题型三 函数定义域的求解
3.(1)已知![]()
![]() 的定义域为
的定义域为![]() ,求函数
,求函数![]() 的定义域;
的定义域;
(2)已知![]()
![]() 的定义域为
的定义域为![]() ,求
,求![]() 的定义域;
的定义域;
(3)已知函数![]()
![]() 的定义域为
的定义域为![]() ,求函数
,求函数![]() 的定义域.
的定义域.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)∵![]() 中的
中的![]()
![]() 的范围与
的范围与![]() 中的x的取值范围相同.
中的x的取值范围相同.
![]() ∴
∴![]() ,
,
![]() ∴
∴![]() ,
,
即![]()
![]() 的定义域为
的定义域为![]() .
.
(2)由题意知![]()
![]() 中的
中的![]() ,
,
![]() ∴
∴![]() .
.
又![]() 中
中![]()
![]() 的取值范围与
的取值范围与![]() 中的x的取值范围相同,
中的x的取值范围相同,
∴![]()
![]() 的定义域为
的定义域为![]() .
.
(3)∵函数![]()
![]() 的定义域为
的定义域为![]() ,
,
由![]()
![]() ,得
,得![]() ,
,
∴![]()
![]() 的定义域为
的定义域为![]() .
.
又![]()
![]() ,即
,即![]() ,
,
∴函数![]()
![]() 的定义域为
的定义域为![]() .
.
![]() 题型四 函数值域的求解
题型四 函数值域的求解
4.高斯是德国著名的数学家,近代数学家奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”设![]() ,用
,用![]() 表示不超过x的最大整数,则
表示不超过x的最大整数,则![]()
![]() 称为高斯函数,例如:
称为高斯函数,例如:![]() ,
,![]() ,已知函数
,已知函数![]() ,
,![]() ,则函数
,则函数![]() 的值域是( )
的值域是( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
![]() 【答案】A
【答案】A
![]() 【解析】
【解析】![]() ,
,
当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]() .
.
∴函数![]()
![]() 的值域是
的值域是![]() .
.
![]() 故选A
故选A
![]() 03题组训练
03题组训练
1.下列从集合![]() 到集合
到集合![]()
![]() 的对应关系中,其中
的对应关系中,其中![]() 是
是![]() 的函数的是
的函数的是
A.![]()
![]() ,对应关系
,对应关系![]() ,其中
,其中![]()
B.![]()
![]() ,对应关系
,对应关系![]() ,其中
,其中![]()
C.![]()
![]() ,对应关系
,对应关系![]() ,其中
,其中![]()
D.![]()
![]() ,对应关系
,对应关系![]() ,其中
,其中![]()
![]() 【答案】C
【答案】C
【解析】对于![]() ,
,![]()
![]() 中的奇数在
中的奇数在![]() 中无元素与之对应
中无元素与之对应![]() 不是
不是![]() 的函数;
的函数;
对于![]() ,
,![]()
![]() 中每个元素在
中每个元素在![]() 中都有两个不同元素对之对应,
中都有两个不同元素对之对应,![]() 不是
不是![]() 的函数;
的函数;
对于![]() ,
,![]()
![]() 中每个元素在
中每个元素在![]() 中都有唯一元素与之对应,
中都有唯一元素与之对应,![]() 是
是![]() 的函数;
的函数;
对于![]() ,
,![]() 中
中![]()
![]() 在
在![]() 中没有元素对应,
中没有元素对应,![]() 不是
不是![]() 的函数,故选C.
的函数,故选C.
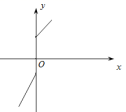
2![]() .如图中,能表示函数
.如图中,能表示函数![]() 的图象的是( )
的图象的是( )
A. 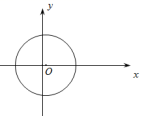
![]() B.
B. 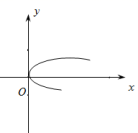
C.![]()
 D.
D.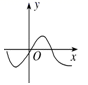
![]() 【答案】D
【答案】D
【解析】由函数定义可知,任意作一条垂直于![]() x轴的直线
x轴的直线![]() ,则直线与函数的图象至多有一个交点,
,则直线与函数的图象至多有一个交点,
根据题意,对于A、![]() B两图,可以找到一个x与两个y对应的情形;
B两图,可以找到一个x与两个y对应的情形;
对于C![]() 图,当x=0时,有两个y值对应;
图,当x=0时,有两个y值对应;
对于D![]() 中图象能表示y是x的函数.
中图象能表示y是x的函数.
![]() 故选:D.
故选:D.
![]() 3.用区间表示下列集合:
3.用区间表示下列集合:
![]() (1)
(1)![]() ______;
______;
![]() (2)
(2)![]() ______;
______;
![]() (3)
(3)![]() ______.
______.
【答案】![]()
![]()
![]()
![]()
【解析】![]() (1)根据集合与区间的改写,可得
(1)根据集合与区间的改写,可得![]() .
.
(2)由![]()
![]() 或
或![]() .
.
(3)由![]()
![]() 或
或![]() .
.
4.已知![]()
![]() ,且
,且![]() ,则
,则![]() ______.
______.
![]() 【答案】
【答案】![]()
【解析】由题意,函数![]() ,令
,令![]()
![]() ,解得
,解得![]() ,则
,则![]() .
.
![]() 故答案为:
故答案为:![]() .
.
5.若函数![]() 满足对任意实数
满足对任意实数![]() ,
,![]()
![]() 都有
都有![]() ,且
,且![]() ,则
,则![]() ______.
______.
![]() 【答案】321
【答案】321
【解析】由题意,函数![]() 满足
满足![]()
![]() ,令
,令![]() ,得
,得![]() ,
,
又![]()
![]() ,所以
,所以![]() ,
,
又![]()
![]() ,则
,则![]() .
.
当![]()
![]() 取
取![]() 时,得
时,得![]() ,
,
![]() 所以
所以![]() .
.
![]() 6.求下列函数的定义域.
6.求下列函数的定义域.
![]() (1)
(1)![]() ;
;
![]() (2)
(2)![]() .
.
【答案】(1) ![]()
![]() (2)
(2) ![]()
【解析】(1)由题意,函数![]() 满足
满足![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() 所以该函数的定义域为
所以该函数的定义域为![]() .
.
![]() (2)由函数
(2)由函数![]() 有意义,
有意义,
则满足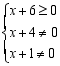 ,即
,即![]()
![]() ,解得
,解得![]() 或
或![]() 或
或![]() ,
,
所以函数![]()
![]() 的定义域是
的定义域是![]() .
.
![]()
人教A版 (2019)必修 第一册3.1 函数的概念及其表示导学案: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000267_t4/?tag_id=42" target="_blank">3.1 函数的概念及其表示导学案</a>,共4页。
高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案: 这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式优质学案,文件包含同步学案高中数学人教版2019必修第一册--课时53考点诱导公式原卷版docx、同步学案高中数学人教版2019必修第一册--课时53考点诱导公式解析版docx等2份学案配套教学资源,其中学案共13页, 欢迎下载使用。
高中人教A版 (2019)5.2 三角函数的概念优质学案: 这是一份高中人教A版 (2019)5.2 三角函数的概念优质学案,文件包含同步学案高中数学人教版2019必修第一册--课时521考点三角函数的概念原卷版docx、同步学案高中数学人教版2019必修第一册--课时522考点同角三角函数的基本关系原卷版docx、同步学案高中数学人教版2019必修第一册--课时521考点三角函数的概念解析版docx、同步学案高中数学人教版2019必修第一册--课时522考点同角三角函数的基本关系解析版docx等4份学案配套教学资源,其中学案共19页, 欢迎下载使用。