


- 【同步导学案】高中数学人教A版(2019)选修第一册-- 2.4.1圆的标准方程 导学案(有答案) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)选修第一册-- 2.4.2圆的一般方程 导学案(有答案) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)选修第一册-- 2.5.2圆与圆的位置关系 导学案(有答案) 学案 2 次下载
- 【同步导学案】高中数学人教A版(2019)选修第一册-- 3.1.1椭圆及其标准方程 导学案(有答案) 学案 6 次下载
- 【同步导学案】高中数学人教A版(2019)选修第一册-- 3.1.2椭圆方程及性质的应用 导学案(有答案) 学案 5 次下载
【同步导学案】高中数学人教A版(2019)选修第一册-- 2.5.1直线与圆的位置关系 导学案(有答案)
展开2.5.1 直线与圆的位置关系
【学习目标】
1.理解直线和圆的三种位置关系.
2.会用代数与几何两种方法判断直线和圆的位置关系.
【学习过程】
一、课前预习
预习课本P91~95,思考并完成以下问题
1.直线与圆的位置关系有哪几种?
2.过圆外一点和圆上一点的切线的方程应分别怎样求?
3.直线被圆所截得的弦长公式是什么?弦长公式是怎样推导出来的?
二、课前小测
1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交
2.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y+1)2=1
C.(x+2)2+(y-1)2=1
D.(x-3)2+(y-1)2=1
3.圆x2+y2-2x+4y-20=0截直线5x-12y+c=0所得的弦长为8,则c的值是( )
A.10 B.10或-68
C.5或-34 D.-68
三、新知探究
直线Ax+By+C=0(A2+B2≠0)与圆(x-a)2+(y-b)2=r2(r>0)的位置关系及判断
位置关系 | 相交 | 相切 | 相离 | |
公共点个数 | 2 | 1 | 0 | |
判 定 方 法 | 几何法:设圆心到直线的距离 d= | d<r | d=r | d>r |
代数法:由 消元得到一元二次方程,判别式为Δ | Δ>0 | Δ=0 | Δ<0 | |
图形 |
|
|
| |
四、题型突破
题型一 直线和圆位置关系的判断
[例1] 已知动直线l:y=kx+5和圆C:(x-1)2+y2=1,那么k为何值时,直线l与圆C相离、相切、相交?
反思感悟
“代数法”与“几何法”判断直线与圆的位置关系,是从不同的方面,不同的思路来判断的,“代数法”侧重于“数”,是从方程角度考虑,计算较为烦琐;“几何法”侧重于“形”,是从几何的角度考虑,方法较为简单,是判断直线与圆的位置关系的常用方法.
跟踪训练
1.对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )
A.相离 B.相切
C.相交但直线不过圆心 D.相交且直线过圆心
题型二 切线问题
[例2] (1)若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
A.2 B.3
C.4 D.6
(2)过点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,求切线l的方程为________________.
反思感悟
(1)过圆上一点(x0,y0)的圆的切线方程的求法
先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为-,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程y=y0或x=x0.
(2)过圆外一点(x0,y0)的切线方程的求法
设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径建立方程,可求得k,也就得切线方程.当用此法只求出一个方程时,另一个方程应为x=x0,因为在上面解法中不包括斜率不存在的情况,而过圆外一点的切线有两条.一般不用联立方程组的方法求解.
(3)求切线长最小值的两种方法
①(代数法)直接利用勾股定理求出切线长,把切线长中的变量统一成一个,转化成函数求最值;
②(几何法)把切线长最值问题转化成圆心到直线的距离问题.
跟踪训练
2.圆x2+y2=4在点P(,-1)处的切线方程为( )
A. x+y-2=0 B. x+y-4=0
C. x-y-4=0 D. x-y+2=0
题型三 弦长问题
[例3] (1)直线y=x被圆x2+(y-2)2=4截得的弦长为________.
(2)直线y=kx+3与圆(x-1)2+(y-2)2=4相交于M,N两点,|MN|≥2,则k的取值范围是________.
(3)已知圆C:x2+y2=4,过定点M(1,1)的直线l交圆C于A、B两点,则|AB|最大值是________,最小值是________.
反思感悟
求直线与圆相交时弦长的两种方法
(1)几何法:如图1,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有2+d2=r2,即|AB|=2.
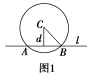
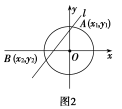
(2)代数法:如图2所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),则|AB|= =|x1-x2|=|y1-y2|(直线l的斜率k存在).
跟踪训练
3.过点(-4,0)作直线l与圆x2+y2+2x-4y-20=0交于A、B两点,如果|AB|=8,求直线l的方程.
五、达标检测
1.过点(-2,0)且倾斜角为的直线l与圆x2+y2=5相交于M、N两点,则线段MN的长为( )
A.2 B.3 C.2 D.6
2.M(3,0)是圆x2+y2-8x-2y+10=0内的一点,过M点最长的弦所在直线方程是( )
A.x+y-3=0 B.x-y-3=0
C.2x-y-6=0 D.2x+y-6=0
3.以点(2,-1)为圆心,且与直线3x-4y+5=0相切的圆的方程为( )
A.(x-2)2+(y+1)2=3
B.(x+2)2+(y-1)2=3
C.(x+2)2+(y-1)2=9
D.(x-2)2+(y+1)2=9
六、本课小结
1.判断直线和圆的位置关系的两种方法中,几何法要结合圆的几何性质进行判断,一般计算较简单.而代数法则是通过解方程组进行消元,计算量大,不如几何法简捷.
2.一般地,在解决圆和直线相交时,应首先考虑圆心到直线的距离,弦长的一半,圆的半径构成的直角三角形.还可以联立方程组,消去x或y,组成一个一元二次方程,利用方程根与系数的关系表达出弦长l=·=|x1-x2|.
3.研究圆的切线问题时要注意切线的斜率是否存在.过一点求圆的切线方程时,要考虑该点是否在圆上.当点在圆上,切线只有一条;当点在圆外时,切线有两条.
参考答案
课前小测
1.答案:D
2.答案:A
3.答案:B
题型突破
[例1] 解析:
解法一 (代数法)联立方程
得(k2+1)x2+(10k-2)x+25=0,则Δ=b2-4ac=(10k-2)2-4(k2+1)·25=-40k-96,故当直线l与圆C相离时,有-40k-96<0,得k>-;
当直线l与圆C相切时,有-40k-96=0,得k=-;
当直线l与圆C相交时,有-40k-96>0,得k<-.
解法二 (几何法)圆C:(x-1)2+y2=1的圆心为C(1,0),半径r=1.
设直线l与圆心C的距离为d,则d=.
当d>r,即>1,k>-时,直线l与圆C相离;
当d=r,即=1,k=-时,直线l与圆C相切;
当d<r,即<1,k<-时,直线l与圆C相交.
跟踪训练
1.解析:
解法一 ∵x2+y2=2的圆心(0,0)到直线y=kx+1的距离d==≤1,又∵r=,∴0<d<r.
∴直线与圆相交但直线不过圆心.
解法二 直线y=kx+1表示过定点(0,1)且斜率存在的动直线,又定点(0,1)在圆x2+y2=2内部,
∴直线与圆相交但直线不过圆心.
答案:C
[例2] 解析:
(1) 因为过圆外一点的圆的切线长l、半径长r和这点到圆心的距离d满足勾股定理,即l2=d2-r2,所以切线长最短时该点到圆心的距离最小,转化成求该点与圆心的距离的最小值问题.由题意易知圆心C(-1,2),半径长r=,点(a,b)在直线y=x-3上,所以点(a,b)与圆心的距离的最小值即圆心到直线y=x-3的距离d,易求d==3,所以切线长的最小值为==4.
(2) ∵(-1-2)2+(4-3)2=10>1,
∴点A在圆外.
当直线l的斜率不存在时,l的方程是x=-1,不满足题意.
设直线l的斜率为k,则切线l的方程为y-4=k(x+1),即kx-y+4+k=0.
圆心(2,3)到切线l的距离为=1,
解得k=0或k=-,
因此,所求直线l的方程为y=4或3x+4y-13=0.
答案:(1)C (2)y=4或3x+4y-13=0
跟踪训练
2.解析:∵()2+(-1)2=4,
∴点P在圆上.
∵切点与圆心连线的斜率为-,
∴切线的斜率为,
∴切线方程为y+1=(x-),
即x-y-4=0.
答案:C
[例3] 解析:
(1)解法一 几何法:圆心到直线的距离为d==,圆的半径r=2,所以弦长为l=2×=2=2;
解法二 代数法:联立直线和圆的方程
消去y可得x2-2x=0,所以直线和圆的两个交点坐标分别为(2,2),(0,0),弦长为=2.
(2) 因为|MN|≥2,所以圆心(1,2)到直线y=kx+3的距离不大于=1,即≤1,
解得k≤0.
(3) 当直线l过圆心时,即如图EF,弦长取得最大值2r=4;
当OM⊥l时,即如图PQ,
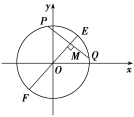
弦长取得最小值=2=2=2
答案:(1)2 (2)k≤0 (3)4 2
跟踪训练
3.解析:将圆的方程配方得(x+1)2+(y-2)2=25,由圆的性质可得,圆心到直线l的距离d==3.
当l的斜率不存在时,x=-4满足题意.
当l的斜率存在时,设方程为y=k(x+4),
即kx-y+4k=0.
由点到直线的距离公式得3=,
解得k=-.
所以直线l的方程为5x+12y+20=0.
综上,所求直线方程为x+4=0或5x+12y+20=0.
达标检测
1.解析:∵l:y=x+2,即x-y+2=0,
又(0,0)到l的距离d==,
∴|MN|=2=2.
答案:C
2.解析:∵M在圆内,∴过M点的最长弦所在的直线应过圆心(4,1).设直线的斜率为k,则k=1,
∴直线方程为x-y-3=0.
答案:B
3.解析:圆心到直线3x-4y+5=0的距离d==3,即圆的半径为3,所以所求圆的方程为(x-2)2+(y+1)2=9.
答案:D
高中数学3.1 椭圆优秀学案设计: 这是一份高中数学3.1 椭圆优秀学案设计,共10页。学案主要包含了学习目标,学习过程等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册3.1 椭圆优秀学案: 这是一份人教A版 (2019)选择性必修 第一册3.1 椭圆优秀学案,共12页。学案主要包含了学习目标,学习过程等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册3.1 椭圆优秀学案: 这是一份人教A版 (2019)选择性必修 第一册3.1 椭圆优秀学案,共11页。学案主要包含了学习目标,学习过程等内容,欢迎下载使用。













