数学九年级上册22.1.1 二次函数优秀教学设计
展开22.1 二次函数的图象和性质
22.1.2 二次函数y=ax2的图象和性质
一、教学目标
【知识与技能】
1.会用描点法画二次函数y=ax2的图象,理解抛物线的有关概念;
2.掌握二次函数y=ax2的性质,能确定二次函数y=ax2的表达式.
【过程与方法】
通过画出简单的二次函数探索出二次函数y=ax2的性质及图象特征.
【情感态度与价值观】
使学生经历探索二次函数y=ax2图象性质的过程,培养学生观察、思考、归纳的良好思维习惯.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
1.二次函数y=ax2的图象的画法及性质;
2.能确定二次函数y=ax2的解析式.
【教学难点】
1.用描点法画二次函数y=ax2的图象,探索其性质;
2.能依据二次函数y=ax2的有关性质解决问题.
五、课前准备
课件、三角尺、铅笔等.
六、教学过程
(一)导入新课
1.你们喜欢打篮球吗?(出示课件2)
2.你们知道投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
学生自主思考.
(二)探索新知
探究一:二次函数y=ax2的图象的画法
出示课件4:画出二次函数y=x2的图象.
学生分组画y=x2的图象,教师巡视,对于不正确的给予指导.
⑴列表:在y=x2中自变量x可以是任意实数,列表表示几组对应值:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y=x2 | … |
|
|
|
|
|
|
| … |
⑵描点:根据表中x,y的数值在坐标平面中描点(x,y)(出示课件5)
⑶连线:如图,再用平滑曲线顺次连接各点,就得到y=x2的图象.
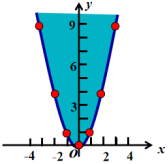
当取更多个点时,函数y=x2的图象如下:(出示课件6)
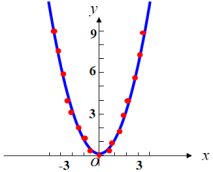
教师归纳:二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.这条抛物线关于y轴对称,y轴就是它的对称轴.对称轴与抛物线的交点叫做抛物线的顶点.
出示课件7:画出二次函数y=-x2的图象.
学生分组画y=-x2的图象,教师巡视,对于不正确的给予指导.
⑴列表:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y=-x2 | … |
|
|
|
|
|
|
| … |
⑵描点:
⑶连线:
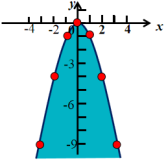
探究二:二次函数y=ax2的图象性质
出示课件8:教师问:根据你以往学习函数图象性质的经验,说说二次函数y=x2的图象有哪些性质,并与同伴交流.

学生交流后,师生共同总结如下:
1.y=x2的图象是一条抛物线;
2.图象开口向上;
3.图象关于y轴对称;
4.顶点( 0 ,0 );
5.图象有最低点.
出示课件9:教师问:说说二次函数y=-x2的图象有哪些性质,并与同伴交流.

学生交流后,师生共同总结如下:
1.y=-x2的图象是一条抛物线;
2.图象开口向下;
3.图象关于y轴对称;
4.顶点(0,0);
5.图象有最高点.
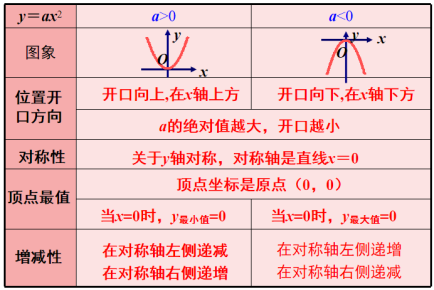
教师归纳:(出示课件10)二次函数y=ax2的图象性质:
1.顶点都在原点(0,0);
2.图像关于y轴对称;
3.当a>0时,开口向上;当a<0时,开口向下.
师生共同探究:观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?(出示课件11)
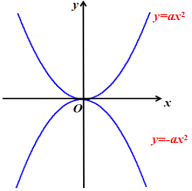
教师强调:二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
探究三:二次函数y=ax2的性质
出示课件12:观察图形,y随x的变化如何变化?

教师归纳:(出示课件13)对于抛物线y=ax2(a>0),
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
师生共同探究:观察图形,y随x的变化如何变化?(出示课件14)
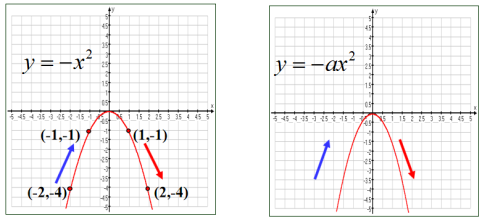
教师归纳:(出示课件15)对于抛物线 y =ax2(a<0)
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
出示课件16:在同一直角坐标系中,画出函数![]() 的图象.
的图象.
将全班同学进行适当分组,分别完成两个图象的画图,并结合图象给予恰当的描述.
解:分别填表,再画出它们的图象,如图:
x | ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ··· |
| ··· |
|
|
|
|
|
|
|
|
| ··· |
x | ··· | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | ··· |
| ··· |
|
|
|
|
|
|
|
|
| ··· |
出示课件17:师生共同探究:二次函数![]() 的图象开口大小与a的大小有什么关系?
的图象开口大小与a的大小有什么关系?
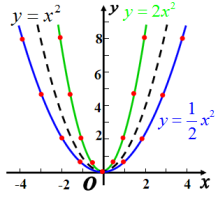
教师归纳:当a>0时,a越大,开口越小.
出示课件18:在同一直角坐标系中,画出函数![]() 的图象.
的图象.
将全班同学进行适当分组,分别完成两个图象的画图,并结合图象给予恰当的描述.
解:分别填表,再画出它们的图象,如图:
x | ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ··· | |
| ··· |
|
|
|
|
|
|
|
|
| ··· | |
x | ··· | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | ··· |
| ··· |
|
|
|
|
|
|
|
|
| ··· |
出示课件19:师生共同探究:二次函数![]() 的图象开口大小与a的大小有什么关系?
的图象开口大小与a的大小有什么关系?

教师归纳:当a<0时,a越小(即a的绝对值越大),开口越小.
对于抛物线y=ax2,|a|越大,抛物线的开口越小.
师生共同完善认知:(出示课件20)
出示课件21:填一填:
(1)函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ;
(2)函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
⑶函数y=![]() x2的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
x2的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;
⑷函数y=-0.2x2的图象的开口 ,对称轴是 ,顶点是 .
学生独立思考后,口答如下:
⑴向上;y轴;(0,0)
⑵向下;y轴;(0,0);高
⑶向上;y轴;(0,0);低
⑷向下;y轴;(0,0)
出示课件22:例 已知y=(m+1)xm2+m是二次函数,且其图象开口向上,求m的值和函数解析式.
学生自主思考后,师生共同解答如下:
解: 依题意有:![]()
解②,得m1=-2,m2=1.
由①,得m>-1.
因此m=1.
此时,二次函数为y=2x2.
出示课件23:已知![]() 是二次函数,且当x>0时,y随x增大而增大,则k= .
是二次函数,且当x>0时,y随x增大而增大,则k= .
学生独立思考后,自主解答如下:
解:![]() 是二次函数,即二次项的系数不为0,x的指数等于2.又因当x>0时,y随x增大而增大,即说明二次项的系数大于0. 因此,
是二次函数,即二次项的系数不为0,x的指数等于2.又因当x>0时,y随x增大而增大,即说明二次项的系数大于0. 因此,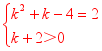 ,解得k=2.
,解得k=2.
探究四:二次函数y =ax2的实际应用
出示课件24:师生共同认知:二次函数y=ax2是刻画客观世界许多现象的一种重要模型.

出示课件25:例 已知正方形的周长为Ccm,面积为Scm2,
(1)求S与C之间的二次函数关系式;
(2)画出它的图象;
(3)根据图象,求出当S=1cm2时,正方形的周长;
(4)根据图象,求出C取何值时,S≥4cm2.
学生独立思考后,师生共同解答.(出示课件26)
解:(1)∵正方形的周长为Ccm,
∴正方形的边长为![]() cm,
cm,
∴S与C之间的关系式为S=![]() ;
;
(2)作图如图:

(3)当S=1cm2时,C2=16,即C=4cm;
(4)若S≥4cm2,即![]() ≥4,解得C≥8,或c≤-8(舍去),因此C ≥ 8cm.
≥4,解得C≥8,或c≤-8(舍去),因此C ≥ 8cm.
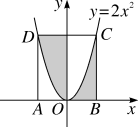
出示课件27:已知二次函数y=2x2.
(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____y2;(填“>”“=”或“<”);
(2)如图,此二次函数的图象经过点(0,0),长方形ABCD的顶点A、B在x轴上,C、D恰好在二次函数的图象上,B点的横坐标为2,求图中阴影部分的面积之和.
学生独立思考后,自主解答:(出示课件28)
(2)解:∵二次函数y=2x2的图象经过点C,
∴当x=2时,y=2×22=8.
∵抛物线和长方形都是轴对称图形,且y轴为它们的对称轴,
∴OA=OB,
∴在长方形ABCD内,左边阴影部分面积等于右边空白部分面积,
∴S阴影部分面积之和=2×8=16.
教师总结如下:(出示课件29)
二次函数y=ax2的图象关于y轴对称,因此左右两部分折叠可以重合,在二次函数比较大小中,我们根据图象中点具有的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较;对于求不规则的图形面积,采用等面积割补法,将不规则图形转化为规则图形以方便求解.
(三)课堂练习(出示课件30-34)
1.已知抛物线y=ax2(a>0)过点A(-2,y1),B(1,y2)两点,则下列关系式一定正确的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y2>y1>0
2.函数y=2x2的图象的开口 , 对称轴 ,顶点是 ;
在对称轴的左侧,y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .
3.函数y=-3x2的图象的开口 , 对称轴 ,顶点是 ;
在对称轴的左侧,y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .

4.如图,观察函数y=(k-1)x2的图象,则k的取值范围是 .

5.说出下列抛物线的开口方向、对称轴和顶点:
| 开口方向 | 对称轴 | 顶点坐标 |
|
|
| |
|
|
| |
|
|
| |
|
|
|
6.已知二次函数y=x2,若x≥m时,y最小值为0,求实数m的取值范围.
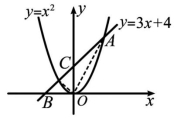
7.已知:如图,直线y=3x+4与抛物线y=x2交于A、B两点,求出A、B两点的坐标,并求出两交点与原点所围成的三角形的面积.
参考答案:
1.C
2.向上;y轴;(0,0);减小;增大
3.向下;y轴;(0,0);增大;减小
4.k>1
5.
| 开口方向 | 对称轴 | 顶点坐标 |
向上 | y轴 | (0,0) | |
向下 | y轴 | (0,0) | |
向上 | y轴 | (0,0) | |
向下 | y轴 | (0,0) |
6.解:在二次函数y=x2中,a=1>0
因此当x=0时,y有最小值.
∵当x≥m时,y最小值=0,
∴m≤0.
7.解:由题意得![]()
解得![]()
因此两函数的交点坐标为A(4,16)和B(-1,1).
∵直线y=3x+4与y轴相交于点C(0,4),即CO=4.两交点与原点所围成的三角形面积S△ABO=S△ACO+S△BOC.在△BOC中,OC边上的高就是B点的横坐标值的绝对值1;在△ACO中,OC边上的高就是A点的横坐标值的绝对值4.
因此S△ABO=S△ACO+S△BOC=![]() ×4×1+
×4×1+![]() ×4×4=10.
×4×4=10.
(四)课堂小结
1.画二次函数y=ax2的图象时,有哪些地方是你需关注的?
2.你是如何理解并熟记抛物线y=ax2的性质的?
3.本节课你还存在哪些疑问?.
(五)课前预习
预习下节课(22.1.3第1课时)的相关内容.
七、课后作业
1.教材41页习题22.1第3,4题
2.配套练习册内容
八、板书设计:

九、教学反思:
本课时的设计比较注重让学生动手操作,让学生通过画二次函数的图象初步掌握其性质,画图的过程中需注意引导学生与其他函数的图象与性质进行对比.本课的目的是要让学生通过动手操作,经历探索归纳的思维过程,逐步获得图象传达的信息,熟悉图象语言,进而形成函数思想.
初中人教版22.1.2 二次函数y=ax2的图象和性质教案及反思: 这是一份初中人教版22.1.2 二次函数y=ax2的图象和性质教案及反思,共4页。教案主要包含了情境导入,初步认识,思考探究,获取新知,运用新知,深化理解,师生互动,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数教学设计: 这是一份初中数学人教版九年级上册22.1.1 二次函数教学设计,共2页。教案主要包含了提出问题,范例,做一做,归纳,课堂练习,作业等内容,欢迎下载使用。
人教版九年级上册22.1.1 二次函数教学设计: 这是一份人教版九年级上册22.1.1 二次函数教学设计,共3页。教案主要包含了情境导入,合作探究,板书设计等内容,欢迎下载使用。