初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径公开课教学设计

24.1 圆的有关性质

24.1.2 垂直于弦的直径

一、教学目标

【知识与技能】

1.通过观察实验，使学生理解圆的轴对称性.

2.掌握垂径定理及其推论.理解其证明，并会用它解决有关的证明与计算问题.

【过程与方法】

通过探索垂径定理及其推论的过程，进一步体会和理解研究几何图形的各种方法.

【情感态度与价值观】

1.结合本课特点，向学生进行爱国主义教育和美育渗透.

2.激发学生探究、发现数学问题的兴趣和欲望.

二、课型

新授课

三、课时

1课时。

四、教学重难点

【教学重点】 

垂径定理及其推论，会运用垂径定理等结论解决一些有关证明，计算和作图问题.

【教学难点】 

垂径定理及其推论.

五、课前准备 

课件、图片、直尺等.

六、教学过程

（一）导入新课

你知道赵州桥吗?它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m，你能求出赵州桥主桥拱的半径吗？（出示课件2）

（二）探索新知

探究一  圆的轴对称性

教师问：把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？（出示课件4）

学生通过自己动手操作，归纳出结论：圆是轴对称图形，任何一条直径所在直线都是它的对称轴．

出示课件5：教师问：圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？

学生答：圆是轴对称图形，任意一条直径所在直线都是圆的对称轴.

思考：如何来证明圆是轴对称图形呢？

出示课件6:已知：在⊙O中，CD是直径，AB是弦，CD⊥AB，垂足为E．

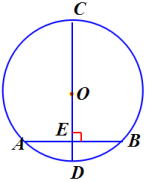
教师问：此图是轴对称图形吗？

学生答：是轴对称图形．

教师问：满足什么条件才能证明圆是轴对称图形呢？

师生共同解答如下：（出示课件7）

证明：连结OA、OB.

则OA＝OB．

又∵CD⊥AB，

∴直径CD所在的直线是AB的垂直平分线.

∴对于圆上任意一点，在圆上都有关于直线CD的对称点，即⊙O关于直线CD对称.

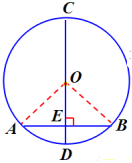
师生进一步认知：圆是轴对称图形，任何一条直径所在直线都是圆的对称轴.

探究二  垂径定理及其推论

出示课件8：如图，AB是⊙O的一条弦, 直径CD⊥AB, 垂足为E.你能发现图中有哪些相等的线段和劣弧?为什么?

学生独立思考后口答：线段:AE=BE

弧:=,=

学生简述理由：把圆沿着直径CD折叠时，CD两侧的两个半圆重合，点A与点B重合，AE与BE重合，重合．

教师总结归纳：（出示课件9）

垂径定理：垂直于弦的直径平分弦,并且平分弦所对的两条弧.

推导格式：∵CD是直径，CD⊥AB，

∴ AE=BE, =,=

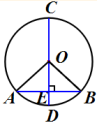
教师强调：垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.

想一想：下列图形是否具备垂径定理的条件？如果不是，请说明为什么？（出示课件10）

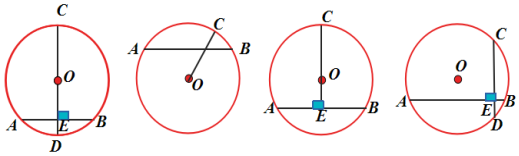
学生独立思考后口答：1图是；2图不是，因为没有垂直；3图是；4图不是，因为CD没有过圆心.

教师强调：垂径定理的几个基本图形：（出示课件11）

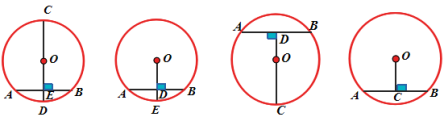
出示课件12：如果把垂径定理（垂直于弦的直径平分弦，并且平分弦所对的两条弧）结论与题设交换一条，命题是真命题吗？

①过圆心；②垂直于弦；③平分弦；④平分弦所对的优弧；⑤平分弦所对的劣弧.

上述五个条件中的任何两个条件都可以推出其他三个结论吗？

学生思考后教师总结：

深化认知：（出示课件13）如图，①CD是直径；②CD⊥AB，垂足为E；③AE=BE；④=;⑤=.举例证明其中一种组合方法.

学生思考后独立解决，并加以交流，教师加以指导，并举例.（出示课件14）

如图，AB是⊙O的一条弦，作直径CD，使AE=BE.

（1）CD⊥AB吗？为什么？

⑵与相等吗？与相等吗？为什么？

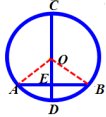
证明：⑴连接AO,BO,则AO=BO,

又AE=BE，OE=OE

∴△AOE≌△BOE（SSS），

∴∠AEO=∠BEO=90°，

∴CD⊥AB.

（2）由垂径定理可得=,=

教师归纳总结：（出示课件15）

垂径定理的推论：平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.

思考：“不是直径”这个条件能去掉吗？如不能，请举出反例.

教师强调：圆的两条直径是互相平分的.

出示课件16：例1 如图，OE⊥AB于E，若⊙O的半径为10cm,OE=6cm,则AB=

      cm.

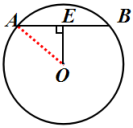
学生思考后师生共同解答：连接OA，∵OE⊥AB，

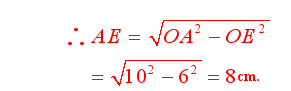
巩固练习：（出示课件17）

如图，⊙O的弦AB＝8cm，直径CE⊥AB于D，DC＝2cm，求半径OC的长.

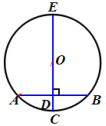
学生自主思考后，独立解答如下：

解：连接OA，∵CE⊥AB于D，

                            ，

∴

设OC=xcm，则OD=x-2,根据勾股定理，得

x2=42+(x-2)2，

解得x=5，

即半径OC的长为5cm.

出示课件18：例2  已知：⊙O中弦AB∥CD,

求证：

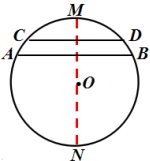
学生思考后师生共同解答.

证明：作直径MN⊥AB.

∵AB∥CD，∴MN⊥CD.

则（垂直于弦的直径平分弦所对的弧）

教师强调：平行弦夹的弧相等.

师生共同归纳总结：（出示课件19）

解决有关弦的问题，经常是过圆心作弦的弦心距（垂线段），或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件.

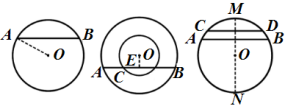
巩固练习：（出示课件20）

如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证: 四边形ADOE是正方形．

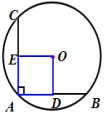
学生独立解答，一生板演.

证明：∵OE⊥AC，OD⊥AB，AB⊥AC，

∴∠OEA=∠EAD=∠ODA=90°.

∴四边形ADOE为矩形，AE=AC,AD=AB.

又∵AC=AB,

∴AE=AD.

∴ 四边形ADOE为正方形.

出示课件21：例3 根据刚刚所学，你能利用垂径定理求出导入中赵州桥主桥拱半径的问题吗?

教师引导学生分析题意，先把实际问题转化为数学问题，然后画出图形进行解答.

解：如图，用AB表示主桥拱，设AB所在圆的圆心为O，半径为R.经过圆心O作弦AB的垂线OC垂足为D，与弧AB交于点C，则D是AB的中点，C是弧AB的中点，CD就是拱高.

∴AB=37m，CD=7.23m.

∴AD=AB=18.5m，OD=OC-CD=R-7.23.

OA2=AD2+OD2，

R2=18.52+(R-7.23)2，

解得R≈27.3.

即主桥拱半径约为27.3m.

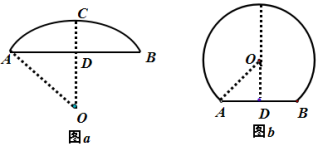
巩固练习:（出示课件23）

如图a、b,一弓形弦长为cm，弓形所在的圆的半径为7cm，则弓形的高为_______.

学生独立思考后解答：如图，分两种情况，弓形的高为5cm或12cm.

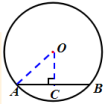
教师归纳：1.涉及垂径定理时辅助线的添加方法（出示课件24）

在圆中有关弦长a,半径r, 弦心距d（圆心到弦的距离），弓形高h的计算题时，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.

2.弓形中重要数量关系

弦a，弦心距d，弓形高h，半径r之间有以下关系：

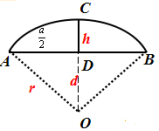
⑴    d+h=r；⑵.

（三）课堂练习（出示课件25-29）

1.

2.已知⊙O中，弦AB=8cm，圆心到AB的距离为3cm，则此圆的半径为         .

3.⊙O的直径AB=20cm, ∠BAC=30°则弦AC=         .

4.（分类讨论题）已知⊙O的半径为10cm，弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为         .

5.已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点.你认为AC和BD有什么关系？为什么？

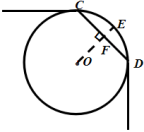
6.如图，一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD，垂足为F,EF=90m.求这段弯路的半径.

参考答案：

1.C

2.5cm

3.

4.14cm或2cm

5.证明：过O作OE⊥AB，垂足为E，

则AE＝BE，CE＝DE.

∴AE－CE＝BE－DE.

即AC＝BD.

6.解:连接OC.

设这段弯路的半径为Rm,则OF=(R-90)m.

，

根据勾股定理，得

解得R=545.

∴这段弯路的半径约为545m.

（四）课堂小结

通过这节课的学习，你有哪些收获和体会？

（五）课前预习

预习下节课（24.1.3）的相关内容.

七、课后作业

配套练习册内容

八、板书设计：

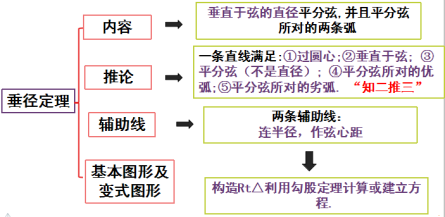
九、教学反思：

1.这节课的教学从利用垂径定理来解决赵州桥桥拱半径问题开始，引入课题从实验入手，得到圆的轴对称性，进而推出垂径定理及推论.教学设计中，从具体、简单、特殊到抽象、复杂、一般，层层递进，以利于提高学生的数学思维能力，同时，注意加强对学生的启发和引导，培养学生们大胆猜想，小心求证的科学研究素质.

2.本课的教学方法是将垂径定理和勾股定理有机结合，将圆的问题转化为直角三角形，常作的辅助线是半径或垂直于弦的直径.