初中数学人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程公开课教学设计
展开22.2.5一元二次方程根与系数的关系
学习目标:
1.理解并掌握根与系数关系:![]() ,
,![]() ;
;
2.会用根的判别式及根与系数关系解题.
重点、难点
重点:理解并掌握根的判别式及根与系数关系.
难点:会用根的判别式及根与系数关系解题;
【课前预习】阅读教材P40 — 42 , 完成课前预习
1、知识准备
( 1 ) 一元二次方程的一般式:
(2)一元二次方程的解法:
(3)一元二次方程的求根公式:
2、探究1:完成下列表格
方 程 |
|
|
|
|
| 2 |
| 5 |
|
x2+3x-10=0 |
|
| -3 |
|
问题:你发现什么规律?
①用语言叙述你发现的规律;
②x2+px+q=0的两根![]() ,
,![]() 用式子表示你发现的规律。
用式子表示你发现的规律。
探究2:完成下列表格
方 程 |
|
|
|
|
2x2-3x-2=0 | 2 |
|
| -1 |
3x2-4x+1=0 |
| 1 |
|
|
问题:上面发现的结论在这里成立吗?
请完善规律;
①用语言叙述发现的规律;
② ax2+bx+c=0的两根![]() ,
,![]() 用式子表示你发现的规律。
用式子表示你发现的规律。
3、利用求根公式推到根与系数的关系(韦达定理)
ax2+bx+c=0的两根![]() = ,
= , ![]() =
=
![]()
![]()
= =
= =
= =
= =
练习1:根据一元二次方程的根与系数的关系,求下列方程的两根和与两根积:
(1)![]() (2)
(2)![]() (3)
(3)![]()
【课堂活动】
活动1:预习反馈
活动2:典型例题
例1:不解方程,求下列方程的两根和与两根积:
(1)x2-6x-15=0 (2)3x2+7x-9=0 (3)5x-1=4x2
例2:已知方程![]() 的一个根是 -3 ,求另一根及K的值。
的一个根是 -3 ,求另一根及K的值。
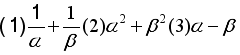 例3:已知α,β是方程x2-3x-5=0的两根,不解方程,求下列代数式的值
例3:已知α,β是方程x2-3x-5=0的两根,不解方程,求下列代数式的值
例4:已知关于x的方程3x2-5x-2=0,且关于y的方程的两根
是x方程的两根的平方,则关于y的方程是__________
活动3:随堂训练
(1)x2-3x=15 (2)5x2-1=4x2+x
(3)x2-3x+2=10 (4)4x2-144=0
(5)3x(x-1)=2(x-1) (6)(2x-1)2=(3-x)2
活动4:课堂小结
一元二次方程的根与系数的关系:
【课后巩固】
一、填空
1. 若方程![]() (a≠0)的两根为
(a≠0)的两根为![]() ,
,![]() 则
则![]() = ,
= ,![]() = __
= __
2 .方程![]() 则
则![]() = ,
= ,![]() = __
= __
3 .若方程![]() 的一个根2,则它的另一个根为____ p=____
的一个根2,则它的另一个根为____ p=____
4 .已知方程![]() 的一个根1,则它的另一根是____ m= ____
的一个根1,则它的另一根是____ m= ____
5 .若0和-3是方程的![]() 两根,则p+q= ____
两根,则p+q= ____
6 .在解方程x2+px+q=0时,甲同学看错了p,解得方程根为x=1与x=-3;乙同学看错了q,解得方程的根为x=4与x=-2,你认为方程中的p=——,q=——。
二、选择
1 .两根均为负数的一元二次方程是 ( )
A![]() B
B![]() C
C![]() D
D![]()
2 .若方程![]() 的两根中只有一个为0,那么 ( )
的两根中只有一个为0,那么 ( )
A p=q=0 B P=0,q≠0 C p≠0,q=0 D p≠0, q≠0)
三、不解方程,求下列方程的两根和与两根积:
(1)x2-5x-10=0 (2)2x2+7x+1=0
(3)3x2-1=2x+5 (5)x(x-1)=3x+7
(5)x2-3x+1=0 (6)3x2- 2x=2
初中数学华师大版九年级上册5.一元二次方程的根与系数的关系教案: 这是一份初中数学华师大版九年级上册5.一元二次方程的根与系数的关系教案,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点等内容,欢迎下载使用。
湘教版九年级上册2.1 一元二次方程公开课教案设计: 这是一份湘教版九年级上册2.1 一元二次方程公开课教案设计,共7页。教案主要包含了教材分析,学情分析,教学目标,教学重点,教学过程等内容,欢迎下载使用。
初中数学人教版九年级上册21.1 一元二次方程获奖教案设计: 这是一份初中数学人教版九年级上册21.1 一元二次方程获奖教案设计,共7页。教案主要包含了教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。