人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称精品教案
展开课题 | 23.2.2中心对称图形 | |||||
课型 | 新授课 | 班级 |
| 姓名 |
| |
学习 目标 | 1.掌握中心对称图形的定义. 2.准确判断某图形是否为中心对称图形. | |||||
学习 重难点 | 掌握中心对称图形的定义. 准确判断某图形是否为中心对称图形. | |||||
教学流程 | 学 案 | 学法指导 | ||||
自主先学 | 1.如果一个图形沿一条直线折叠,直线两旁的部分能够互相 ,这个图形就叫做轴对称图形。 2.把一个图形绕着某一点旋转 ,如果它能够与另一个图形 ,那么这 图形成中心对称。 | 自学课本第66至67页.思考什么样的图形是中心对称图形. | ||||
合作探究
跟踪训练
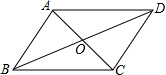
| (1) 如图,将线段AB绕它的中心点旋转180°,你有什么发现?
结论:观察上图可以发现,线段AB绕它的中心旋转180°后与 重合. (2)如图,将平行四边形ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
结论:观察上图可以发现,平行四边形ABCD绕它的两条对角线的交点O旋转180°后 与 重合. 归纳:(1)把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形 ,那么这个图形叫做 .这个点就是它的 . (3)中心对称与中心对称图形的区别与联系:中心对称反映_____个图形之间的位置关系,中心对称图形反映的是_____个图形的特征,它们都是通过把图形旋转______度重合来判断的,两者可以相互转化。联系:
1、下列几何图形: (1)等腰三角形 (2)矩形 (3)等腰梯形 (4)平行四边形,其中是中心对称图形的是 。 2、角是 对称图形,线段是_ 对称图形,又是_ 对称图形。 3、下列数字是中心对称图形的是( ) A.4 B.2 C.3 D.0 4、下列图形中,既是轴对称图形,又是中心对称图形的是( ) A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形 5、所有的平行四边形都是_______对称图形;奇数边的正多边形只是 对称图形;偶数边的正多边形都是______对称图形,又是_ 对称图形。 6、在英文字母VWXYZ中,是心对称的英文字母的个数有( )个. A.1 B.2 C.3 D.4 7、扑克牌中,黑桃2,黑桃9,方块5,梅花3是中心对称图形的是
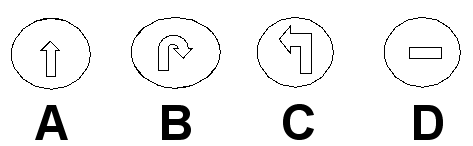
8. 写出三个中心对称的汉字 。 9、下列汽车标志中,可以看作是中心对称图形的是( )
10、下列图形中既是轴对称图形是中心对称图形的是( )
|
小组讨论后,观看幻灯片,再得出结论。
| ||||
拓展训练
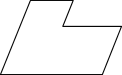
| 如果公园里的草坪是下面的形状,你能否只修一条笔直的小路就将这块草坪分成面积相等的两部分?
|
| ||||
总结反思
|
|
| ||||
课后作业 |
课本67页2、69页2. |
| ||||
初中数学人教版九年级上册23.2.2 中心对称图形教案: 这是一份初中数学人教版九年级上册23.2.2 中心对称图形教案,共6页。
初中人教版23.2.2 中心对称图形教案: 这是一份初中人教版23.2.2 中心对称图形教案,共5页。
初中数学人教版九年级上册23.2.2 中心对称图形教案设计: 这是一份初中数学人教版九年级上册23.2.2 中心对称图形教案设计,共3页。教案主要包含了教学目标,教学过程等内容,欢迎下载使用。