【同步教案】人教版数学八年级上册--11.1.2三角形的高、中点、角平分线 教案

第十一章 三角形

11.1.2三角形的高、中线、角平分线

一、内容和内容解析

1.内容

了解三角形的高、中线、角平分线等有关概念，掌握三角形的高、中线与角平分线的画法．

2.内容解析

给出三角形的高、中线与角平分线的概念。结合会用工具准确画出三角形的高、中线与角平分线，这是对学生尺规作图要求的进一步提高，在原有的过一点画一条直线的垂线知识基础上，增加图形难度，画三角形的高是学生学习的难度，如何用转化的思想解决这个问题，是本节课要传递给学生的重要数学思想。另外通过画图了解三角形的三条高(及所在的直线)交于一点，三角形的三条中线，三条角平分线等都交于一点．

基于以上分析，确定本节课的教学重点是：画三角形的高、中线与角平分线.

二、目标和目标分析

1.目标

（1）了解三角形的高、中线、角平分线等有关概念及性质；

（2）掌握三角形的高、中线与角平分线的画法；

（3）了解三角形的三条高、三条中线、三条角平分线分别交于一点．

2.目标分析

达成目标（1）的标志是：学生清晰地知道，三角形的高、中线、角平分线所带来的相应的数量关系，通过定义让学生感知由形到数的过度，数形不分家的数学特点；

目标（2）体现在学生能用三角板、直尺、量角器做出钝角三角形、锐角三角形、直角三角形的高、中线、角平分线，这三种几何作图为后面辅助线的添加做好铺垫；

目标（3）通过观察作图，得出三角形的三条高、三条中线、三条角平分线分别交于一点这一结论.

三、教学问题诊断分析

1．学生已学习了角的平分线和过一点做已知线段的垂线，所以本节课所学的角平分线、高要与之相类比，发现相同与不同之处，对于三角形的中线，学生也有线段中点的知识做铺垫，才可以在原有知识的基础上更好的掌握新知识.但是对于学生来说，动手操作作图是比较难掌握。

基于以上分析，确定本节课的教学难点是：三角形角平分线、中线、高的作图．

四、教学过程设计

一、复习回顾

复习本节课需要类比学习的三个知识点：线段中点、角平分线、垂线的定义及作图.

创设情景，明确目标

你还记得“过一点画已知直线的垂线”吗？让学生动手操作，画一画．在此基础上再提问：过三角形的一个顶点，你能画出它的对边的垂线吗？从而引入课题．

二、三角形的高

(1) 你能画出这个三角形的三条高吗?

(2) 你能用折纸的办法得到它们吗?

(3) 这三条高之间有怎样的位置关系？

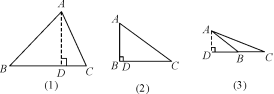
展示点评：三角形的高是什么线？三个图形中的高有什么区别？同一个三角形有几条高？他们在位置上有什么关系？请分别画出各个三角形的高．

小组讨论：三角形的高的交点位置有何特征？

反思小结：锐角三角形的高在三角形内部，直角三角形有两条高在边上，钝角三角形有两条高在三角形外部．任意三角形都有三条高，并且三条高所在的直线相交于一点．

三角形的高的表示法

∵AD是△ ABC的高

∴∠ BDA = ∠ CDA =90°

　三角形的中线

活动二：任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?

三角形的中线的表示法

∵AD是△ABC的中线

∴BD=CD= 0.5BC

　三角形的角平分线

活动三：动手画出锐角三角形、直角三角形和钝角三角形的三角的角平分线．

展示点评：学生分组合作画图，师生共同点评．

小组讨论：三角形的角平分线是什么线？与角平分线有什么区别？一个三角形有几条角平分线？它们在位置上有什么关系？

反思小结：任何三角形有三条角平分线，并且都在三角形的内部交于一点，我们把这个交点叫做三角形的内心．三角形的角平分线是一条线段，而角平分线是一条射线．

三角形的平分线的表示法

∵AD是 △ ABC的角平分线

∴∠ BAD = ∠ CAD =0.5∠BAC

活动四：三角形的角平分线与角的平分线有什么区别？

三角形的角平分线是一条线段 , 角的平分线是一条射线

三、总结梳理，内化目标

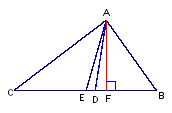
1.如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,

CF⊥AD于H,判断下列说法是否正确.

①AD是△ABE的角平分线 (   )

②BE是△ ABD边AD上的中线(   )

③BE是△ ABC边AC上的中线(   )

④CH是△ ACD边AD上的高(   )

1、下列各组图形中，哪一组图形中AD是△ABC 的高(    )

2、如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（   ）

A.锐角三角形     B.直角三角形     C.钝角三角形     D.锐角三角形

3.如图，在ΔABC中，AE是中线，AD是角平分线，AF是高。

填空：

（1）BE=      =0.5       ；

（2）∠BAD=               =                 ；

（3）∠AFB=               =90°；

拓展练习

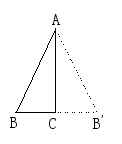1.如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′ 

的位置,则线段AC具有性质(   )

 A.是边BB′上的中线     

 B.是边BB′上的高

 C.是∠BAB′的角平分线  

 D.以上三种性质合一

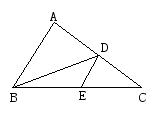2.如图所示,D,E分别是△ABC的边AC、BC的中点,下列说法不正确的是(      )

    A. DE是△BCD的中线   

    B.BD是△ABC的中线

    C.AD=DC,BE=EC       

    D.∠C的对边是DE

四、作业布置

1．课本P8　3、4、8.

    2. 如何把一个三角形分成4个面积相等的三角形