

初中数学人教版八年级上册15.2.3 整数指数幂一等奖第一课时教学设计
展开15.2.3整数指数幂(1)教学设计
教学目标
1. 了解负整数指数幂的概念.
2. 掌握整数指数幂的运算性质,会进行简单的整数指数幂的运算
教学重点
掌握整数指数幂的运算性质
教学难点
会运用整数指数幂进行运算
教学过程设计
一. 复习引入:
1、 还记得正整数指数幂的意义吗?正整数指数幂有哪些运算性质呢?
师生活动:教师提问,学生思考,回顾正整数指数幂的运算性质。
![]() (m、n是正整数)
(m、n是正整数)
![]() (m、n是正整数)
(m、n是正整数)
![]() (n是正整数)
(n是正整数)
![]() (
(![]() 0,m、n是正整数,)
0,m、n是正整数,)
![]()
(n是正整数)
![]() 2、零指数:规定 (
2、零指数:规定 (![]() )
)
3、将正整数指数幂的运算性质中指数的取值范围由“正整数”扩大到“整数”,这些性质还适用吗?
设计意图:通过复习,为下面的探究内容作铺垫。
二、互动新授
思考1 一般地,![]() 中m指数可以是负整数吗?如果可以,那么负整数指数幂
中m指数可以是负整数吗?如果可以,那么负整数指数幂![]() 表示什么?
表示什么?
填空:
![]()
![]()
问题 由填空的结果,你有什么发现?
师生活动:教师引导学生根据除法的意义、分式的约分及同底数幂的运算性质填空,
![]() 并得出结论:
并得出结论:
教师归纳:为了使上述运算性质适用范围更广,同时也可以更简便地表示分式,数学中规定:
![]() 一般地,当n是正整数时, 这就是说
一般地,当n是正整数时, 这就是说![]() 是
是![]() 的倒数
的倒数
像上面这样,引入负整数指数幂后,指数的取值范围就推广到全体整数。
![]()
![]() 思考2 引入负整数指数幂后, 这条性质能否推广到m,n是任意整数的清形呢?
思考2 引入负整数指数幂后, 这条性质能否推广到m,n是任意整数的清形呢?
![]()
![]() 我们从特殊情形入手进行研究,例如:
我们从特殊情形入手进行研究,例如:![]()
即
![]()
![]() 即
即
4、 观察结果,你发现什么规律?
![]() 归纳: 这条性质对于m,n是任意整数的情形仍然适用。
归纳: 这条性质对于m,n是任意整数的情形仍然适用。
探究:类似地,你可以用负整数指数幂或0指数幂对于其他正整数指数幂的运算性质进行试验,看看这些性质在整数指数幂范围是否还适用。
教师指出:事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂。
例9 计算
(1)![]() ;(2)
;(2)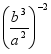 ;(3)
;(3) ![]() ; (4)
; (4) ![]()
师生活动:学生练习后,教师讲评:
![]() 解 (1)
解 (1) ![]() ;
;
![]()
![]()
![]()
![]()
![]()
教师说明:含有负整数指数幂的运算,有两种处理方式:一是把负整数指数幂化为正整数指数幂,然后进行计算,二是在整数指数幂范围内运用幂运算法则进行计算,如果最终结果是负整数指数幂,则应把它化成正整数指数幂。
课堂练习1 填空:
(1) ![]()
![]()
(2) ![]()
![]()
(3) ![]()
![]()
练习2. 判断正误
(1) ![]()
(2) ![]()
练习3.计算
![]() (1)
(1)
![]() (2)
(2)
练习4.下列等式是否正确?为什么?
![]()
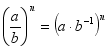 (1)
(1)
(2)
解:![]()
![]() 故等式正确.
故等式正确.
思考3:由这两个等式,能否将整数指数幂的5条性质进行适当合并?
归纳结论
![]() (1)
(1)
结论:同底数幂的除法可转化为同底数幂的乘法
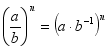 (2)
(2)
结论:商的乘方可转化为积的乘方
这样,整数指数幂的运算性质可以归结为:
![]() (m、n是整数)
(m、n是整数)
![]() (m、n是整数)
(m、n是整数)
![]() (n是整数)
(n是整数)
设计意图:由学生回顾、类比正整数指数幂的运算性质,经历探索负整数指数幂和零指数幂的运算性质的过程,进一步体会幂的意义,发展学生代数推理能力和有条理的表达能力。
:5、课堂小结
教师与学生一起回顾本节课的学习,你有什么收获?
本节课主要学习了:
![]() 1.负整数指数幂:任何不等于0的数的0次幂等于1,即
1.负整数指数幂:任何不等于0的数的0次幂等于1,即![]() ,任何不等于0的-n(n为正整数)次幂,等于这个数的n次幂的倒数,即
,任何不等于0的-n(n为正整数)次幂,等于这个数的n次幂的倒数,即
2.将运算性质的适用范围由正整数指数幂推广到整数指数幂,并由5条性质归结为3条性质。
设计意图:引导学生总结自己的收获,培养学生表达、归纳、反思的能力。
6、作业布置
完成课本相应练习。
板书设计:
15.2.3 整数指数幂(1)
![]() 负整数指数幂
负整数指数幂
当n是正整数时,
初中数学人教版八年级上册15.2.3 整数指数幂精品第二课时教学设计及反思: 这是一份初中数学人教版八年级上册15.2.3 整数指数幂精品第二课时教学设计及反思,共3页。
初中数学人教版八年级上册15.2.3 整数指数幂教案: 这是一份初中数学人教版八年级上册15.2.3 整数指数幂教案,共5页。教案主要包含了复习,预习自测,探究案,当堂检测,课堂小结,作业等内容,欢迎下载使用。
人教版八年级上册15.2.3 整数指数幂教学设计: 这是一份人教版八年级上册15.2.3 整数指数幂教学设计,共4页。














