人教版八年级上册12.1 全等三角形优秀教学设计

第十二章 三角形全等

12.2三角形全等判定复习课

一、内容和内容解析

1.内容

本章复习内容分为三个课时：第一课时：全等三角形；第二课时：全等三角形的判定； 第三课时：角的平分线的性质

2.内容解析

《全等三角形的判定》的学习，是在学生学习了三角形的有关要素和性质、全等图形的特征的基础上进行的，它是证明线段相等、角相等的重要方法，同时为今后探索直角三角形全等的条件及三角形相似的条件提供很好模式和方法，因此，从一定意义上说，本节内容的学习是学生学好几何切入点之一。

基于以上分析，确定本节课的教学重点是：利用SSS SAS ASA AAS HL定理证明三角形全等.

二、目标和目标分析

1.目标

（1）熟练掌握全等三角形的4种判定方法，并能灵活运用；

（2）在全等三角形的说理过程中，重视学生逻辑思维的发展，重视文字语言、符号语言、图形语言的相互转译，并能正确书写推理过程；

（3）让学生在逻辑说理过程中体验成功的感觉，培养学生学习几何的兴趣。

三、教学问题诊断分析

学生已具备了探究三角形全等条件的基础知识，基本知识掌握扎实，学习热情高，主动探究意识强，课堂参与主动、积极。学习这节课的目的是为了提高学生运用全等三角形的判定解决问题的能力。选择建构理论中支架式教学策略，通过搭建梯度恰当的问题脚手架，引导教学的进行，从而使学生掌握、建构和内化所学知识，进行较高水平的认知活动，获得深层次的认知体验

基于以上分析，确定本节课的教学难点是：全等三角形的说理过程中，学生逻辑思维的发展，以及文字语言、符号语言、图形语言的相互转译．

四、教学过程设计

活动一、复习本章知识结构图

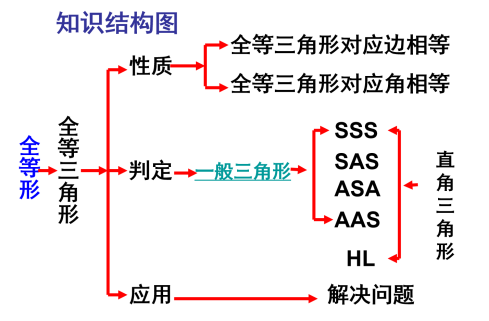
设计意图：

通过梳理知识结构，才能使知识系统化、网络化，形成知识一体化，做到用时一条线，有点有面。

知识梳理1

三角形全等判定方法1：三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）

知识梳理2

三角形全等判定方法2：两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)

知识梳理3

三角形全等判定方法3：有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”）。

知识梳理4

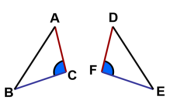
思考:在△ABC和△DFE中,当∠A=∠D , ∠B=∠E和AC=DF时,能否得到 △ABC≌△DFE?

三角形全等判定方法4：有两角和其中一个角的对边对应相等的两个三角形全等(可以    简写成“角角边”或“AAS”）。

思考:在△ABC和△ABD中,能否得到 △ABC≌△ABD?

结论：SSA不能判断两三角形全等

知识梳理5

三角形全等判定方法5：直角三角形全等判定：HL

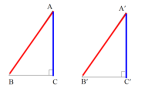
活动二、复习全等三角形中的基本图形

(1)平移后全等

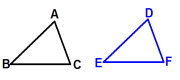
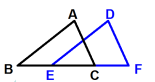
反思小结：相关题型 课本P15第2题、课本P16 第9题、课本P27 第8题

(2)    旋转后全等

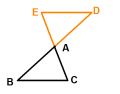
反思小结：相关题型 课本P16 第10题 、课本P26 第3题

(3)    翻折后全等

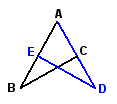
反思小结：相关题型 课本P10第2题、 课本P13 第2题、课本P15 第3题

(4)    找复杂图形中的基本图形

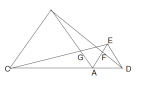
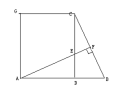
设计意图：知道了这几种基本图形，那么在解决全等三角形问题时，就容易从复杂的图形中分解出基本图形，解题就会变得简便。

综合运用

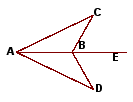例1.如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是           .

分析：现在我们已知 A→∠CAB=∠DAB；S→ AB=AB(公共边)

      ①用SAS,需要补充条件AD=AC,     

      ②用ASA,需要补充条件∠CBA=∠DBA, 

      ③用AAS,需要补充条件∠C=∠D, 

      ④此外,补充条件∠CBE=∠DBE也可以(?)

练习1.:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是         。

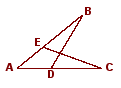
练习2：如图,已知∠1=∠2,AC=AD,增加下列件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有(        )个.      

设计意图：这几个题属于开放题，答案不唯一，通过这几个题的训练，使学生能灵活运用全等三角形的判定解题。

例2.已知：如图，AB=AC,AD=AE, ∠1=∠3，那么∠E=∠D吗？为什么？

.

变式：

1.已知：如图，AB=AC,AD=AE, 请你再添一个条件，使得∠E=∠D？为什么？

2.已知：如图，AB=AC, ∠1=∠3, 请你再添一个条件，使得∠E=∠D？为什么？

设计意图：这道例题的选择是想通过变式，加深了学生对判定方法的灵活应用的同时还调动了学生的积极性。

例3 :如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE

练习：已知：∠ACB=∠ADB=900，AC=AD，P是AB上任意一点，求证：CP=DP

设计意图：让学生加深如何通过全等三角形去求证相等线段。

例4 (2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF,           (1)求证: ΔABC≌ΔDEF;

(2)你还可以得到的结论是         .

(写出一个,不再添加其他线段,不

再表注或使用其他字母)

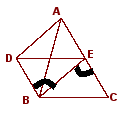
练习.如图,A是CD上的一点,⊿ABC ,⊿ADE  都是正三角形,求证CE=BD

变式1:在原题条件不变的前提下,可以探求以下结论:

(1)求证:AG=AF;

(2)求证:⊿ABF≌⊿ACG;

(3)连结GF,求证⊿AGF是正三角形;

(4)求证GF//CD

变式2:在原题条件下,再增加一个条件,在CE,BD上分别取中点M,N,求证:⊿AMN是正三角形

变式3:如图,点C为线段AB延长线上一点,⊿AMC,⊿BNC为正三角形,且在线段AB同侧,求证AN=MB

分析:此中考题与原题相比较,只是两个三角形的位置不同,此图的两个三角形重叠在一起,增加了难度,其证明方法与前题基本相同,只须证明⊿ABN≌⊿BCM

变式4:如图,⊿ABD,⊿ACE都是正三角形,求证CD=BE

分析:此题实质上是把题目中的条件B,A,C三点改为不

共线,证明方法与前题基本相同.

小结:

1.   证明两个三角形全等，要结合题目的条件和结论，选择恰当的判定方法
   2. 全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时注意：

    ①要观察待证的线段或角，在哪两个可能全等的三角形中。

②分析要证两个三角形全等，已有什么条件，还缺什么条件。

③有公共边的，公共边一定是对应边， 有公共角的，公共角一定是对应角，有对顶角，对顶角也是对应角

2.   注意正确地书写证明格式(顺序和对应关系).

作业：课本P27：7、8、9